吴恩达机器学习
目录
几种激活函数
- 对应于视频的第二课第二周 2.1~2.3,P61~63
- 另参考:
激活函数原理
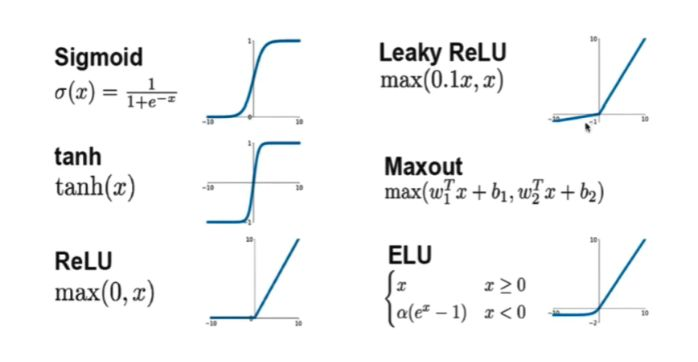
叠加原理:
相当于将上面这些图像进行拉伸和平移后,再叠加相加在一起,这就可以模拟出任意曲线,即模拟出任意函数
思想上有点像是泰勒展开和傅里叶变换
这便是机器学习的本质——“找函数”
网络层和输出层的都叫激活函数吗?怎么选择
几种激活函数
激活函数分为
无论用哪种激活函数,都可以用g(z)来表示
常用激活函数

常用的 非线性激活函数
Sigmoid,σ函数
公式
σ(z)=1+e−z1
图像
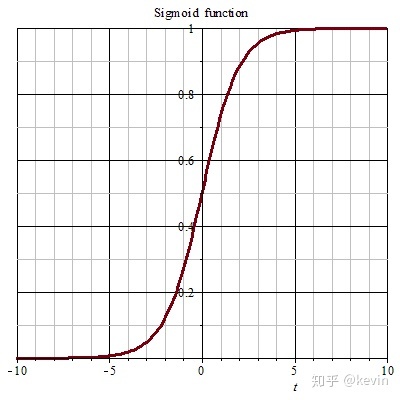
优点
- Sigmoid函数的输出在(0,1)之间,输出范围有限,优化稳定,可以用作输出层。
- 连续函数,便于求导。
缺点
- sigmoid函数在变量取绝对值非常大的正值或负值时会出现梯度饱和现象,意味着函数会变得很平,并且对输入的微小改变会变得不敏感。
在反向传播时,当梯度接近于0,权重基本不会更新,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。 - sigmoid函数的输出不是0均值的,会导致后层的神经元的输入是非0均值的信号,这会对梯度产生影响。
- 计算复杂度高,因为sigmoid函数是指数形式。
Tanh,双曲正切函数
Tanh函数也称为双曲正切函数,是双曲函数中的一个,取值范围[−1,1]
公式
tanh(z)=ez+e−zez−e−z 实际上,Tanh函数是sigmoid的变形:tanh(z)=2σ(z)−1
图像
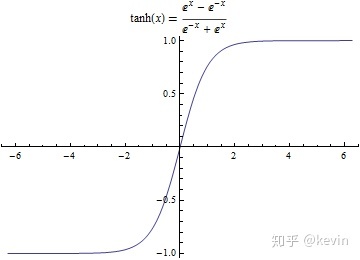
优缺点
- 由于Tanh函数是Sigmoid函数的变形,两者优缺点相似
- Tanh函数是 0 均值的,因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题。
常用的 线性单元类
Linear Activation Function / No Activation Function
线性激活函数,其实也叫做 “没有使用任何激活函数”
g(z)=z,z=w⋅x+b或表示成f(x)=w⋅x+b
ReLU,整流线性单元(Rectified Linear Unit)
ReLU函数(整流线性单元)是现代神经网络中最常用的激活函数,大多数前馈神经网络默认使用的激活函数,常用于隐层神经元输出
公式
ReLU(z)={z0 if z>0 if z≤0或表示成ReLU(z)=max(0,z)
图像
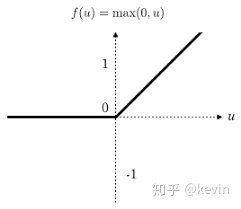
优点
- 快。使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快得多
- 在x>0区域上,不会出现梯度饱和、梯度消失的问题。
- 计算复杂度低。不需要进行指数运算,只要一个阈值就可以得到激活值。
缺点
- ReLU的输出不是0均值的。
- Dead ReLU Problem(神经元坏死现象):ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。
产生这种现象的两个原因:参数初始化问题;learning rate太高导致在训练过程中参数更新太大。
解决方法:采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
Leaky ReLU,渗漏整流线性单元(Leaky ReLU)
是ReLU函数的衍生版本
公式
LeakyReLu(z)=max(0.1z,z)
图像
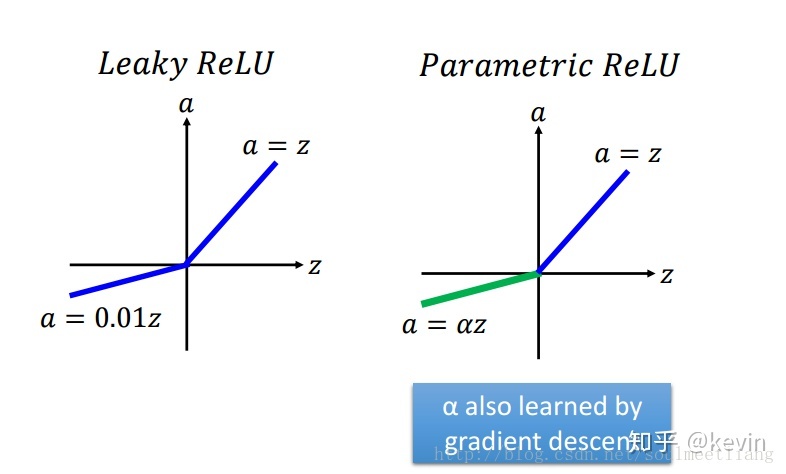
特点
渗漏整流线性单元(Leaky ReLU),为了解决dead ReLU现象。用一个类似0.01的小值来初始化神经元,从而使得ReLU在负数区域更偏向于激活而不是死掉。这里的斜率都是确定的。
leakyrelu激活函数是relu的衍变版本,主要就是为了解决relu输出为0的问题。如图所示,在输入小于0时,虽然输出值很小但是值不为0。 leakyrelu激活函数一个缺点就是它有些近似线性,导致在复杂分类中效果不好。
PReLU,参数整流线性单元(Parametric ReLU)
公式
PReLU(z)=max(az,z)
图像

特点
- 参数整流线性单元(Parametric Rectified linear unit,PReLU),用来解决ReLU带来的神经元坏死的问题。
- 其中(?)不是固定的,是通过反向传播学习出来的。
ELU,指数线性单元(Exponential Linear Unit)
是ReLU函数的衍生版本
ELU(z)={zα(ez−1) if z>0 if z≤0
图像
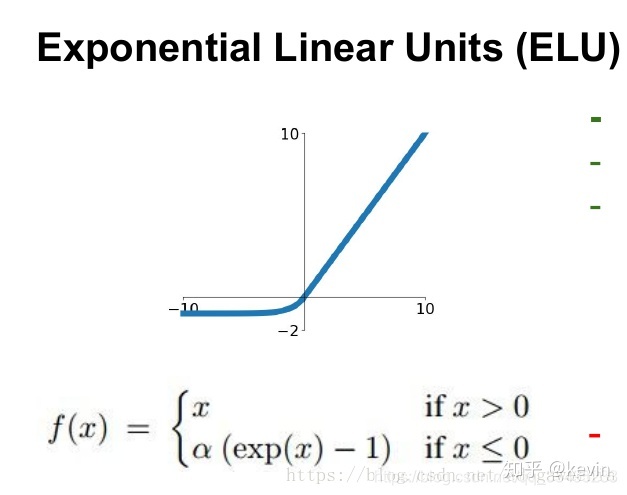
优缺点
可以看做是介于ReLU和Leaky ReLU之间的一个函数
- 具有relu的优势,没有Dead ReLU问题,输出均值接近0,实际上PReLU和Leaky ReLU都有这一优点。
- 有负数饱和区域,从而对噪声有一些鲁棒性。
- 计算量大,因为也需要计算exp
其他
SELU,扩展型指数线性单元(Scaled ELU)
比较新
SELU(z)={λzλα(ez−1) if z>0 if z≤0
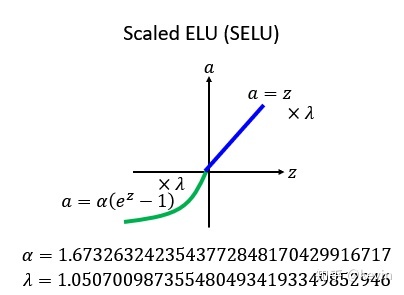
Maxout
maxout是一个函数逼近器
如何选择激活函数
比较
| 激活函数 | 图像 | 补充 | 优缺点、选用 |
|---|
σ
Sigmoid |  | σ(z)=1+e−z1 | 非0均值
两端容易梯度饱和
接近0时容易梯度消失 |
双曲正切函数
Tanh |  | tanh(z)=ez+e−zez−e−z | 0均值
两端容易梯度饱和
接近0时容易梯度消失
_
几乎适用所有场合 |
整流线性单元
ReLU
(Rectified LU)
(LU=Linear Unit) |  | f(z)=max(0,z) | 非0均值
x>0时不会出现梯度饱和/消失 |
渗漏整流线性单元
Leaky ReLU | 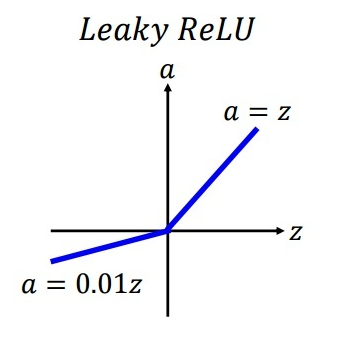 | f(z)=max(0.01z,z) | (同上) |
参数整流线性单元
PReLU
(Parametric ReLU) | 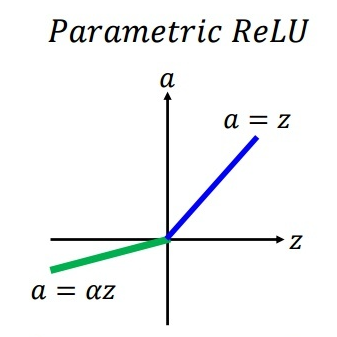 | f(z)=max(az,z) | (同上) |
指数线性单元
ELU
(Exponential LU) |  | f(z)={zα(ez−1)if z>0if z≤0 | (同上) |
扩展型指数线性单元
SELU
(Scaled ELU) |  | f(z)={λzλα(ez−1)if z>0if z≤0 | (同上)
_
比较新 |
| Maxout | | | |
(其中LU为 Linear Unit)
Sigmoid & ReLU
重点比较Sigmoid和ReLU函数
根据需求
- 如果是二元分类(Binary Classification)
- Sigmoid激活函数通常是最优选择(y=0/1)
- 如果是回归问题(Regression)
- 可能会使用线性激活函数(y=+/−)
- 或者使用ReLU类的激活函数(y=0/+),ReLU是最常用的激活函数
横向比较
| 比较项 | Sigmoid | ReLU |
|---|
| 图像 |  |  |
| 计算复杂度 | 高,指数形式 | 低 |
| 收敛速度 | 慢 | 快,SGD算法的收敛速度比 sigmoid 和 tanh 快得多 |
| 梯度饱和&梯度消失 | 会出现
变量取绝对值非常大的正值或负值时会出现梯度饱和现象
在反向传播时当梯度接近于0,很容易就会出现梯度消失的情况 | 不会出现
在x>0区域上,不会出现梯度饱和、梯度消失的问题 |
| 其他 | 不会? | 会出现神经元坏死现象 |
| 输出是0均值 | 不是(Bad) | 不是(Bad) |
| 场景 | 除了输出层是二分类,基本不会使用 | 最常用,如果不确定用哪个激活函数,就用ReLu或Leaky ReLu |
补充、一些大概解释
梯度饱和:函数会变得很平,对输入的微小改变会变得不敏感
梯度消失:权重基本不会更新,从而无法完成深层网络的训练
输出不是0均值的:这是不好的,会导致后层的神经元的输入是非0均值的信号,这会对梯度产生影响
神经元坏死现象(Dead ReLU Problem):
ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。
产生这种现象的两个原因:参数初始化问题;learning rate太高导致在训练过程中参数更新太大。
解决方法:采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
代码字符串
在Tenserflow包中
activation='sigmoid'
activation='linear'
activation='relu'
不同层可以使用不同的激活函数
from tf.kearas.layers import Dense
model = Sequential([
Dense(units=25, activation='relu'), # 隐藏层1
Dense(units=15, activation='relu'), # 隐藏层2
Dense(units= 1, activation='sigmoid') # 输出层
])
为什么模型需要激活函数、为什么需要非线性激活函数
不使用激活函数(即使用的是纯线性激活函数)
我们假设一个神经网络只有两层,每层只有一个单元,那么结果也是线性的:
f(x)=x时(不使用激活函数) a[2]====f(z[2])=f(W[2]∗a[1]+B[2])W[2]∗a[1]+B[2]W[2]∗(W[1]∗x+b[1])+B[2](W[2]W[1])x+W[2]B[1]+B[1]
同理,我们可以类推得知:
Q:激活函数为什么是非线性的?
A:
如果使用线性激活函数,那么输入跟输出之间的关系为线性的,无论神经网络有多少层都是线性组合。
使用非线性激活函数是为了增加神经网络模型的非线性因素,以便使网络更加强大,增加它的能力。
使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。
如果想要进行回归预测,那么
输出层可能会使用线性激活函数,但在隐含层都使用非线性激活函数
不过话说这某个例子里,我们用线性激活函数作为隐藏层,在输出层使用Sigmoid函数。这个神经网络模型,便是相当于是用来处理逻辑回归的
线性激活函数用来作中间层,可以减少变化
激活函数与梯度下降
激活函数的导数
Sigmoid函数
g(z)= dzdg(z)==σ(z)=1+e−z11+e−z1(1−1+e−z1)g(z)(1−g(z)) {当z=10或−10,当z=0,dzdg(z)≈0dzdg(z)=41
tanh函数
g(z)= dzdg(z)=tanh(z)=ez+e−zez−e−z1−(tanh(z))2 {当z=10或−10,当z=0,dzdg(z)≈0dzdg(z)=1-(0)=1
ReLU函数
(注:通常在z= 0的时候给定其导数1,0;当然z=0的情况很少)
g(z)= g(z)′=max(0,z)⎩⎨⎧01undefinedif z < 0if z > 0if z = 0
Leaky ReLU函数
(与ReLU类似)
g(z)= g(z)′=max(0.01z,z)⎩⎨⎧0.011undefinedif z < 0if z > 0if z = 0
梯度下降
正向传播方程如下(之前讲过):
forward propagation:
z[1]=a[1]= z[2]=a[2]=W[1]x+b[1]σ(z[1])W[2]a[1]+b[2]g[2](z[z])=σ(z[2])
反向传播方程如下:
back propagation:
dz[2]=dW[2]=db[2]= dz[1]=dW[1]=(n[1],1)db[1]=A[2]−Y,Y=[y[1]y[2]⋯y[m]]m1dz[2]A[1]Tm1np.sum(dz[2],axis=1,keepdims=True)(n[1],m)W[2]Tdz[2]∗activationfunctionofhiddenlayerg[1]′∗(n[1],m)(z[1])m1dz[1]xTm1np.sum(dz[1],axis=1,keepdims=True)

















