吴恩达深度学习

目录

深层神经网络

深层 (L层) 神经网络

层数

逻辑回归，结构如下图左边。一个隐藏层的神经网络，结构下图右边：

注意，神经网络的层数是这么定义的：从左到右，由0开始定义，比如上边右图，${x}_{1}$、${x}_{2}$、${x}_{3}$,这层是第0层，这层左边的隐藏层是第1层，由此类推。如下图左边是两个隐藏层的神经网络，右边是5个隐藏层的神经网络。

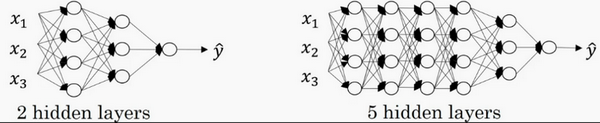
深层和浅层神经网络

在过去的几年中，DLI（深度学习学院 deep learning institute）已经意识到有一些函数，只有非常深的神经网络能学会，而更浅的模型则办不到。

我们再看下深度学习的符号定义：

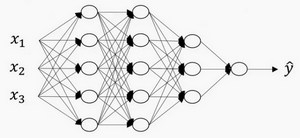
• 层数
  • 我们用L表示，上图中$L=4$
• 神经元数
  • 输入层：索引为 “0”，${n}^{[0]}={n}_{x}=3$
  • 隐藏层：${n}^{[1]}=5$，表示第一个隐藏层有5个隐藏神经元。同理，${n}^{[2]}=5$，${n}^{[3]}=3$
  • 输出层：索引为 "L"，${{n}^{[4]}}$=${{n}^{[L]}}=1$（输出单元为1）
• 激活结果
  • 在不同层所拥有的神经元的数目，对于每层$l$都用${a}^{[l]}$来记作$l$层激活后结果，我们会在后面看到在正向传播时，最终能你会计算出${{a}^{[l]}}$。
  • 通过用激活函数 $g$ 计算${z}^{[l]}$，激活函数也被索引为层数$l$，然后我们用${w}^{[l]}$来记作在l层计算${z}^{[l]}$值的权重。类似的，${{z}^{[l]}}$里的方程${b}^{[l]}$也一样。

最后总结下符号约定：

• 输入的特征记作$x$，但是$x$同样也是0层的激活函数，所以$x={a}^{[0]}$。

• 最后一层的激活函数，所以${a}^{[L]}$是等于这个神经网络所预测的输出结果。

• 但是如果你忘记了某些符号的意义，请看笔记最后的附件：《深度学习符号指南》。

深层神经网络的传播

正向传播

前向传播的步骤可以写成：

$$\begin{align} {z}^{[l]}=& {W}^{[l]}\cdot{a}^{[l-1]}+{b}^{[l]}\\ {{a}^{[l]}}=& {{g}^{[l]}}\left( {{z}^{[l]}}\right) \end{align}$$

前向传播需要喂入${A}^{[0]}$也就是$X$，来初始化

向量化实现过程可以写成：

$$\begin{align} {z}^{[l]}=& {W}^{[l]}\cdot {A}^{[l-1]}+{b}^{[l]}\\ {A}^{[l]}=& {g}^{[l]}({Z}^{[l]}) \end{align}$$

反向传播

（这篇比较难）

反向传播的步骤：

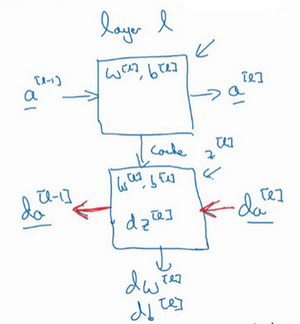
输入为${{da}^{[l]}}$，输出为${{da}^{[l-1]}}$，${{dw}^{[l]}}$, ${{db}^{[l]}}$

反向传播的步骤可以写成：

$$~\begin{align} (1)&& d{{z}^{[l]}}=& d{{a}^{[l]}}*{{g}^{[l]}}'( {{z}^{[l]}})\\ (2)&& d{{w}^{[l]}}=& d{{z}^{[l]}}\cdot{{a}^{[l-1]}}\\ (3)&& d{{b}^{[l]}}=& d{{z}^{[l]}}\\ (4)&& d{{b}^{[l]}}=& d{{z}^{[l]}}\\~\\ (1^*)&& d{{z}^{[l]}}=& {{w}^{[l+1]T}}d{{z}^{[l+1]}}\cdot \text{ }{{g}^{[l]}}'( {{z}^{[l]}}) \end{align}\\ \text{式子（1*）由式子（4）带入式子（1）得到，前四个式子就可实现反向函数}$$

向量化实现过程可以写成：

$$\begin{align} (5)&& d{{Z}^{[l]}}=& d{{A}^{[l]}}*{{g}^{\left[ l \right]}}'\left({{Z}^{[l]}} \right)\\ (6)&& d{{W}^{[l]}}=& \frac{1}{m}\text{}d{{Z}^{[l]}}\cdot {{A}^{\left[ l-1 \right]T}}\\ (7)&& d{{b}^{[l]}}=& \frac{1}{m}\text{ }np.sum(d{{z}^{[l]}},axis=1,keepdims=True)\\ (8)&& d{{A}^{[l-1]}}=& {{W}^{\left[ l \right]T}}.d{{Z}^{[l]}} \end{align}$$

$W$会在每一层被更新为$W=W-α~dW$

$b$ 会在每一层被更新为$b=b-α~db$

搭建神经网络块（Building blocks of deep neural networks）

前向和反向传播

（红色箭头标注标注反向步骤）

多个层连起来就是这样：

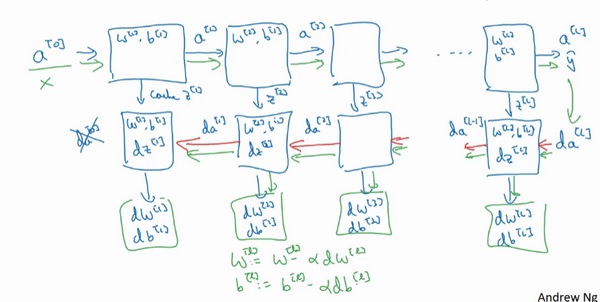
这是神经网络一个梯度下降循环

补充一个细节，那就是把反向函数计算出来的$z$值缓存下来。
当你做编程练习的时候去实现它时，你会发现缓存可能很方便，可以迅速得到$W^{[l]}$和$b^{[l]}$的值

为什么使用深层表示？（Why deep representations?）

这一节我们讲为什么深层的网络在很多问题上比浅层的好
为什么有一些函数，只有非常深的神经网络能学会，而更浅的模型则办不到

深层原理

深度神经网络的这许多隐藏层中，较早的前几层能学习一些低层次的简单特征，等到后几层，就能把简单的特征结合起来，去探测更加复杂的东西。

• 例如人脸识别，几个层依次检测
  • 边缘、五官、人脸
• 例如语音识别：几个层依次检测
  • 音频波形的一些特征：比如音调是变高了还是低了，分辨白噪音，咝咝咝的声音，或者音调，可以选择这些相对程度比较低的波形特征
  • 音位：然后把这些波形组合在一起就能去探测声音的基本单元。在语言学中有个概念叫做音位。
    比如说单词ca，c的发音，“嗑”就是一个音位，a的发音“啊”是个音位，t的发音“特”也是个音位。
  • 单词：有了基本的声音单元以后，组合起来，你就能识别音频当中的单词，
  • 词组：单词再组合起来就能识别词组
  • 句子：再到完整的句子

类比的例子

人脑类比，可能和人脑的原理相同

有些人喜欢把深度神经网络和人类大脑做类比，这些神经科学家觉得人的大脑也是先探测简单的东西，比如你眼睛看得到的边缘，然后组合起来才能探测复杂的物体，比如脸。
这种深度学习和人类大脑的比较，有时候比较危险。但是不可否认的是，我们对大脑运作机制的认识很有价值，有可能大脑就是先从简单的东西，比如边缘着手，再组合成一个完整的复杂物体，这类简单到复杂的过程，同样也是其他一些深度学习的灵感来源，之后的视频我们也会继续聊聊人类或是生物学理解的大脑。

电路类比

另外一个，关于神经网络为何有效的理论，来源于电路理论，它和你能够用电路元件计算哪些函数有着分不开的联系。
根据不同的基本逻辑门，譬如与门、或门、非门。
在非正式的情况下，这些函数都可以用相对较小，但很深的神经网络来计算，小在这里的意思是隐藏单元的数量相对比较小。
但是如果你用浅一些的神经网络计算同样的函数，也就是说在我们不能用很多隐藏层时，你会需要成指数增长的单元数量才能达到同样的计算结果。

浅层与深层

Small：隐藏单元的数量相对较少

Deep：隐藏层数目比较多

深层的网络隐藏单元数量相对较少，隐藏层数目较多。如果浅层的网络想要达到同样的计算结果则需要指数级增长的单元数量才能达到