李宏毅机器学习深度学习

目录

训练原理

对应视频：P3 ~ P4

对应pdf：01_Regression_P1.pdf ~ 02_Regression_P2.pdf

训练的概念

这三个步骤合起来，叫做训练

1. 写出一个带有未知参数的函式
2. 从训练数据中定义 “Loss”
3. 最佳化

具体体现会用下一节的例子来说明

线性模型

例子：

比如我们要预测一个YouTube频道明天的观看次数，机器学习找这个函数的过程分三个步骤

这是一个 Linear Model 的例子，即线性模型

① 写出一个带有未知参数的函式

比如：

$$y=b+wx_1$$

② 从训练数据中定义 “Loss”

定义一个东西叫做Loss，Loss它也是一个Function，那这个Function它的输入是我们Model裡面的参数。
现在如果我们把这一组未知的参数，设定某一个数值的时候能得到L；L是Loss这个Function的输出，值越小表示未知参数越好

常用的Function可以是

• L is mean absoulute error (MAE 平均绝对误差)
• L is mean square error (MSE 均方误差)
• (RMSE 均平方误差)

有点类似于高中学的 "最小二乘法"

③ 最佳化

Optimization，最佳化有很多种方法

• Gradient Descent
• 牛顿法（有点像牛顿法求极值）
• 等等

单隐藏层神经网络

从这个例子中，大概能看得出神经网络是怎么演化来的

① 新模型的 Function

Function with Unknown Parameters

从线性模型到机器学习（模型的改良）

线性模型（旧方案）

就是前面那个例子

$$y=b+wx_1$$

当然这个模型还能继续优化

例如我们会发现每隔七天它一个循环，如果我们一个模型，它是参考前七天的资料。那么我们就可以修改一下我们的模型。
通常一个模型的修改，往往来 自於你对这个问题的理解，也就是Domain Knowledge

激活函数

分段线性 激活函数

Model 的 Bias

但是对于 Linear Model，不管怎麼摆弄w 跟 b，你永远製造不出折线一样的东西
Linear 的 Model 有很大的限制,这一种来自於 Model 的限制,叫做 Model 的 Bias（模型偏差）
之前我们将y=wx+b中的b也叫做 Bias，但这其实有一点 Ambiguous，他们不是同一个意思

这需要一个更复杂的 function，比如 Piecewise Linear的Curves，用多种线性折线的函数叠加来模拟曲线

sigmoid 激活函数

其他激活函数（蓝色function的函数不太好写，后面我们都修改为sigmoid函数）
（这是一种S型的Function，通常用希腊字母 sigma$\sigma$表示）

$$\begin{aligned} sigmoid激活函数：y =& \frac 1{1+e^{-z}}\\ 激活参数：z =& wx+b\\~\\ 合并起来就是： y =& {\color{red}c} \frac 1{1+e^{-({\color{green}b}+{\color{orange}w}x_1)}} \end{aligned}$$

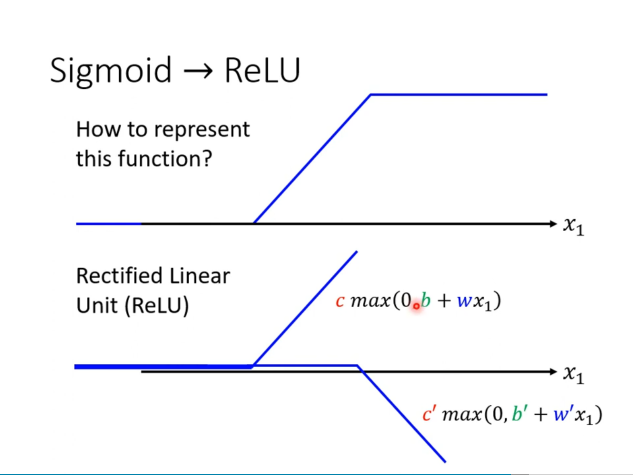
ReLU 激活函数

两个ReLU激活函数相加，其实就可以组成之前说的一个分段线性函数，也有点像是Sigmoid函数

\begin{aligned} y =& b+\sum_i {\color{red}c_i}\times \text{sigmoid}({\color{green}b_i}+\sum_j {\color{\orange}w_{ij}}x_j)\\ y =& b+\sum_{{\color{cyan}2}i} {\color{red}c_i}\times \max(0,{\color{green}b_i}+\sum_j {\color{\orange}w_{ij}}x_j)\\ &\text{（第二条式子的2i只是为了好理解，实际上i是比较任意的）} \end{aligned}

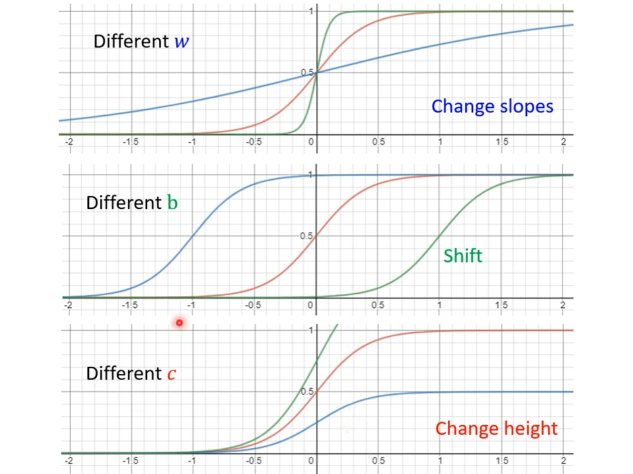
激活函数的参数

三个参数中

• b改变相当沿x轴移动
• w改变相当于x轴缩放
• c改变相当于y轴缩放

图像以simoid函数为例

组合后的函数

公式

这公式相当于一个很简单的神经网络是（单隐藏层神经网络）：输入层 -> Sigmoid隐藏层 -> 线性单输出层，所以有两组w和b（$w_i,b_i,c,b$）

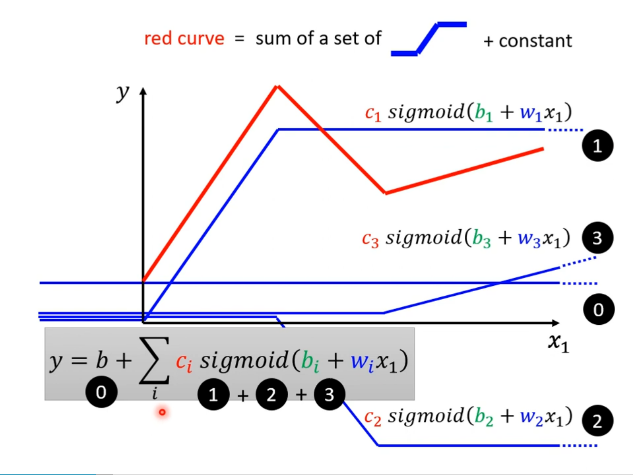
~\begin{aligned} \text{All~Piecewise Linea Curves} =& \text{Constant} + \text{sum of a set of “蓝色的Function”}\\ 所有分段线性曲线 =& 常数 + 一组曲线的和\\ y =& b+\sum_i {\color{red}c_i}\times \sigma({\color{green}b_i}+{\color{\orange}w_i}x_1) \end{aligned}

相较于原来的公式，新的函数更复杂。Curvers 越复杂，转折的点越多，需要的蓝色的 Function 就越多

\begin{aligned} y =& b+wx_i\\ & \downarrow\\ y =& b+\sum_i {\color{red}c_i}\times \sigma({\color{green}b_i}+{\color{\orange}w_i}x_1) \end{aligned}

图像

多个特征的情况

我们可以更进一步减少 Model 的 Bias，写一个更有弹性的有未知参数的 Function
改进点：更多的features（不是只用一个 Feature，而是用多个 Feature，用 $j$ 来代表 Feature 的编号）

\begin{aligned} y =& b+\sum_j w_jx_j\\ & \downarrow\\ y =& b+\sum_i {\color{red}c_i}\times \sigma({\color{green}b_i}+\sum_j {\color{\orange}w_{ij}}x_j) \end{aligned}

比如设定为三个特征：x1 代表前一天的观看人数，x2 两天前观看人数，x3 三天前的观看人数

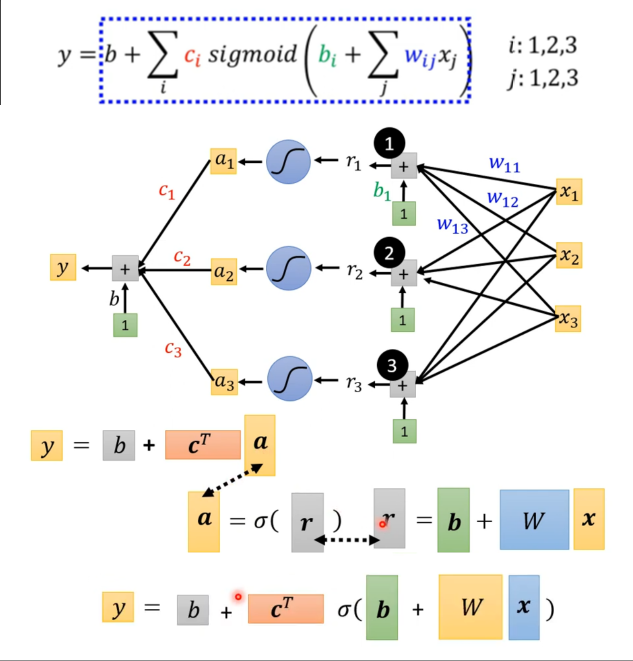
多个特征的情况 - 向量化

然后这个新的公式又可以简化成矩阵，

$r$的公式向量化：（$r$表示一个中间变量，在吴恩达的课里面该符号是$z$而不是$r$）

$$\left\{\begin{matrix} r_1=b_1+w_{11}x_1+w_{12}x_2+w_{13}x_3\\ r_2=b_2+w_{21}x_1+w_{22}x_2+w_{23}x_3\\ r_3=b_3+w_{31}x_1+w_{32}x_2+w_{33}x_3 \end{matrix}\right.\\ \downarrow\\ \begin{bmatrix} r_1\\r_2\\r_3 \end{bmatrix} = \begin{bmatrix} b_1\\b_2\\b_3 \end{bmatrix} + \begin{bmatrix} w_{11}&w_{12}&w_{13}\\ w_{21}&w_{22}&w_{23}\\ w_{31}&w_{32}&w_{33} \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix}\\~\\ \mathbf{r}~~~~=~~~\mathbf{b}~~~+~~~~~\mathbf{W}\mathbf{x}~~~~~~~~~~~~~~~~~~~~~~~~~~$$

y 的公式向量化：

$$~ \begin{aligned} \mathbf{r} =& \mathbf{b}+\mathbf{W}\mathbf{x}\\ \mathbf{a} =& \sigma(\mathbf{r})\\ y =& b+\mathbf{c}^T\mathbf{a}\\~\\ 合并后就是：y =& b+\mathbf{c}^T\sigma(\mathbf{b}+\mathbf{W}\mathbf{x}) \end{aligned}\\~\\ 其中~\mathbf{x}~是~feature\\ \mathbf{W},~\mathbf{b},~\mathbf{c}^T,~\mathbf{b}~都是未知参数$$

② 新模型的 Loss

将未知参数排起来，叫$\theta$

$$Loss: L(\theta)$$

③ 新模型的 Optimization

演算法也是差不多

$$\mathbf{\theta}^* = \arg \min_\theta L\\ \mathbf{\theta}=\begin{bmatrix} \theta_1\\\theta_2\\\theta_3\\\vdots \end{bmatrix}$$

符号

$$\begin{aligned} \theta^0，& 参数的随机初始化，这里上标表示第几次迭代的参数\\ g，& 梯度下降方向\\ \bigtriangledown，&求偏导的符号？\\ L，&表示Mini-batch梯度下降法里的batch\\ {\color{red}\eta}，& 学习率（在吴恩达的课里则用{\color{red}\alpha}表示） \end{aligned}$$

梯度下降

$$\begin{aligned} \mathbf{g} =& \bigtriangledown L(\mathbf{\theta}^0)\\ \theta^1:=& \theta^0-{\color{red}\eta} g\\~\\ -----&拆开来表示-----\\~\\ \mathbf{g} =& \begin{bmatrix} \frac{\partial L}{\partial \theta_1}|_{\theta=\theta^0}\\ \frac{\partial L}{\partial \theta_2}|_{\theta=\theta^0}\\ \vdots \end{bmatrix}\\ \begin{bmatrix} \theta_1^1\\ \theta_2^2\\ \vdots \end{bmatrix} :=& \begin{bmatrix} \theta_1^0\\ \theta_2^0\\ \vdots \end{bmatrix} - \begin{bmatrix} {\color{red}\eta}\frac{\partial L}{\partial \theta_1}|_{\theta=\theta^0}\\ {\color{red}\eta}\frac{\partial L}{\partial \theta_2}|_{\theta=\theta^0}\\ \vdots \end{bmatrix} \end{aligned}$$

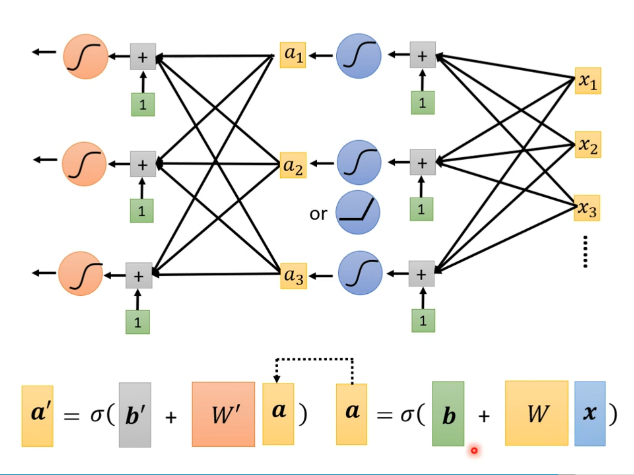
多隐藏层神经网络、深度学习

这里以两个隐藏层为例

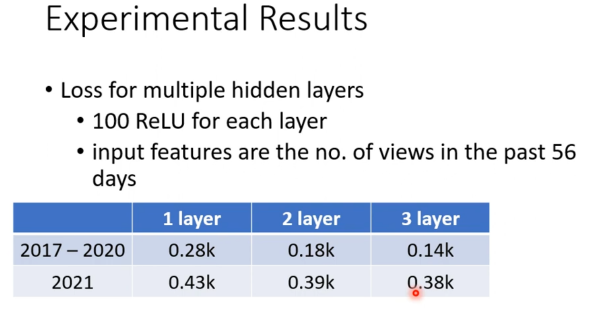
多个层能有效减少Loss损失

一些概念

$$\begin{align} \text{Neuron}：& 网络层里的单元\\ \text{Neural Network}：& 神经网络\\ \text{hidden layout}：& 隐藏层\\ \text{Deep Learning}：& 深度学习，有很多隐藏层 \end{align}$$

深度学习的一些历史

• AlexNet (2012)：8层，错误率 16.4%
• VGG (2014)：19层，映像识别错误率 7.3%
• GoogleNet (2014)：22层，错误率 6.7%
• Residual Net (2015)：152层，错误率 3.57%