做一下别人的校赛

符号规定

设生产瓦楞纸$A$

$$A=\begin{bmatrix} a_{31}&a_{32}&a_{33}&a_{34}\\ a_{51}&a_{52}&a_{53}&a_{54} \end{bmatrix}^T$$

瓦楞纸尺寸$Asize$

$$Asize=\begin{bmatrix} 2500&2500\\ 2000&2000\\ 1800&1800\\ 1500&1500 \end{bmatrix}$$

生产瓦楞纸价格（五层瓦楞板价格为三层板的1.3倍算出）

$$Aw=\begin{bmatrix} 10.0&6.5&4.8&4.0\\ 13.0&8.45&6.24&5.2 \end{bmatrix}^T$$

设生产纸箱个数$B$

$$B=\begin{bmatrix} b_{31}&b_{32}&b_{33}&b_{34}&b_{35}&b_{36}&b_{37}&b_{38}&\cdots\\ b_{51}&b_{52}&b_{53}&b_{54}&b_{55}&b_{56}&b_{57}&b_{58}&\cdots \end{bmatrix}^T$$

纸箱尺寸$Bsize$

$$Bsize=\begin{bmatrix} 530&290&370\\ 530&230&290\\ 430&210&270\\ 350&190&230\\ 290&170&190\\ 260&150&180\\ 230&130&160\\ 210&110&140\\ 195&105&135\\ 175&95&115\\ 145&85&105\\ 130&80&90 \end{bmatrix}$$

生产纸箱约束$Bst$（需求个数）

$$Bst=\begin{bmatrix} 50&67&86&89&108&121&123&129&140&116&96&86\\ 90&95&80&75&70&88&76&79&69&60&65&72 \end{bmatrix}^T$$

生产纸箱售价$Bw$

$$Bw=\begin{bmatrix} 2.96&2.21&1.76&1.35&1.02&0.85&0.68&0.55&0.50&0.39&0.34&0.29\\ 3.78&2.82&2.25&1.71&1.30&1.08&0.87&0.70&0.64&0.53&0.43&0.37 \end{bmatrix}^T$$

合理假设

(1) 假设生产的纸箱为需求数

即假设最优情况时，生产纸箱的个数不会溢出（即便生产多了也卖不出去）且能全部售出给下游快递公司

此时$B=Bst$，$wB=f_{sum}(Bst~\cdot~Bw)=2462.4$，其中定义$f_{sum}$为求矩阵元素和

Matlab表达式：

Bst=[50,67,86,89,108,121,123,129,140,116,96,86;
90,95,80,75,70,88,76,79,69,60,65,72].';
Bw=[2.96,2.21,1.76,1.35,1.02,0.85,0.68,0.55,0.50,0.39,0.34,0.29;
3.78,2.82,2.25,1.71,1.30,1.08,0.87,0.70,0.64,0.53,0.43,0.37].';
wB=sum((sum(Bst.*Bw))') 		% 2462.4

此时售价不变，节约成本以获取最大利润

(2) 纸箱结构假设

假设每个纸箱均有6面，其中长宽面为顶底面

且假设纸箱的6个面只有其中一条侧边可以进行拼接，即纸板都是一体的，不能拼接而成

且假设封顶与封底的突出长度均为较短边（宽边）的一半

纸箱的展开图如下

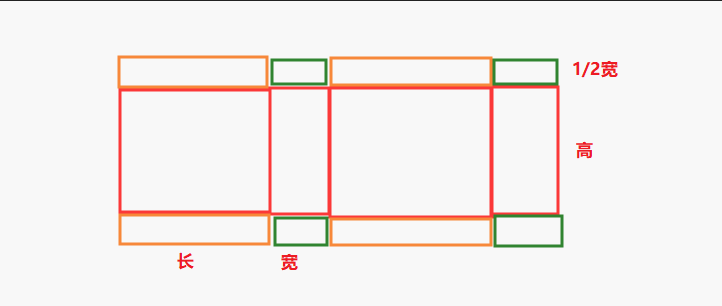
即纸箱需要使用纸板的尺寸$BsizeX=(长+宽)\times2，BsizeY=高+宽$

Matlab表达式：

Bsize=[530,290,370;
530,230,290;
430,210,270;
350,190,230;
290,170,190;
260,150,180;
230,130,160;
210,110,140;
195,105,135;
175,95,115;
145,85,105;
130,80,90];
BsizeArea(:,1)=(Bsize(:,1)+Bsize(:,2)).*2;
BsizeArea(:,2)=(Bsize(:,2)+Bsize(:,3))

即纸箱需要使用纸板的尺寸$BsizeArea$

$$BsizeArea=\begin{bmatrix} 1640&660\\ 1520&520\\ 1280&480\\ 1080&420\\ 920&360\\ 820&330\\ 720&290\\ 640&250\\ 600&240\\ 540&210\\ 460&190\\ 420&170 \end{bmatrix}$$

模型分析

列出每种纸板可能制作的纸箱（每种方案令再无边料可以制作纸箱）（转化为方案问题）

• 纸板1（2500x2500）

  • 方案	1	2	3	4	5	6	7	8	9	10	11	12
    1	3	0	0	0	0	0	0	0	1	0	0	0
    2
    3

• 纸板2（2000x2000）

  • 方案	1	2	3	4	5	6	7	8	9	10	11	12
    1
    2
    3

• 纸板3（1800x1800）

  • 方案	1	2	3	4	5	6	7	8	9	10	11	12
    1
    2
    3

• 纸板4（1500x1500）

  • 方案	1	2	3	4	5	6	7	8	9	10	11	12
    1
    2
    3

线性规划模型

线性规划模型

目标：利润w

$$w$$

subject to

$$s.t.\left\{\begin{aligned} \end{aligned}\right.$$