跳至主要內容

Diffusion模型

Diffusion模型

目录

Diffusion模型

参考：

介绍

Diffusion模型能做什么？

DALL·E介绍

  • 2021年1月，第一版
  • 2022年1月，第二版

与GAN对比

  • 孰是孰非还得等等，目前来看主流的生成模型已经不怎么用GAN了，最新的都是Diffusion Model
  • GAN要训练俩网络，感觉难度 较大，容易不收敛，而且多样性较差，只关注能骗过判别器就行（容易走捷径、或走歪路）
  • Diffusion MOdel用一种更简单的方法来诠释了生成模型该如何学习已经生成，其实感觉更简单

相关论文

  • 主要基于这个来讲：DDPM论文连接：[Ho et al.，2020]
    （DDPM的全程是 Denoising Diffusion Probabilistic Model，最早的引用是2015年了）

原理

大概原理

  • 前向过程，就是不断往输入数据加噪声，最快快变成了个纯噪声
  • 每一个时刻都要添加高斯噪声，后一时刻都是由前一刻增加噪声得到
  • 其实这个过程可以看成我们不断构建标签（噪声）的过程，后续会用到
image-20221020102724598

加噪过程

前向过程的公式：（杂点的增加应该越来越多）

at=1−βtβ要越来越大（论文中0.0001到0.002，从而α会越来越小）一开始加点噪就有效果，越往后得加噪越多才行xt=αtxt−1+1−αtz1递归公式xt−1是前一刻的状态，z1表示噪音，后者权重越来越大\begin{align} & a_t=1-\beta_t && \beta要越来越大（论文中0.0001到0.002，从而\alpha会越来越小）\\ & && 一开始加点噪就有效果，越往后得加噪越多才行\\ & x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_1 && 递归公式\\ & && x_{t-1}是前一刻的状态，z_1表示噪音，后者权重越来越大 \end{align}

递归有点像RNN，有一些缺点，有没有方法不递归直接计算？

简化递归公式（推导）：

∵xt=αtxt−1+1−αtz1∵xt−1=αt−1xt−2+1−αt−1z2 ∴xt=αt(αt−1xt−2+1−αt−1z2)+1−αtz1=αtαt−1xt−2+(αt(1−αt−1)z2)+1−αtz1)=αtαt−1xt−2+1−αtαt−1zˉ2Z1和Z2都浮肿高斯，然后可以进行化简Z1：N (0,1−αt)Z2：N (0,at(1−αt−1))N(0,σ12Ⅰ)+N(0,σ22Ⅰ)∼N(0,(σ12+σ22)Ⅰ)=αˉtx0+1−αˉtzˉt 其中，αˉt=αt⋅αt−1⋯α0（累乘）\begin{aligned} \because x_t =& \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_1\\ \because x_{t-1} =& \sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_2\\~\\ \therefore x_t =& \sqrt{\alpha_t} {\color{red}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_2)} +\sqrt{1-\alpha_t}z_1\\ =& \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + (\sqrt{\alpha_t(1-\alpha_{t-1})}z_2) + \sqrt{1-\alpha_t}z_1)\\ =& \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}}\bar z_2 && Z1和Z2都浮肿高斯，然后可以进行化简\\ &&& Z_1：N~(0,1-\alpha_t)\\ &&& Z_2：N~(0,a_t(1-\alpha_{t-1}))\\ &&& N(0,\sigma_1^2Ⅰ)+N(0,\sigma_2^2Ⅰ) \sim N(0,(\sigma_1^2+\sigma_2^2)Ⅰ)\\ =& \sqrt{\bar\alpha_t}x_{0} + \sqrt{1-\bar\alpha_t}\bar z_t\\~\\ 其中，\bar\alpha_t =& \alpha_t\cdot\alpha_{t-1}\cdots\alpha_0 &&（累乘） \end{aligned}

去噪过程

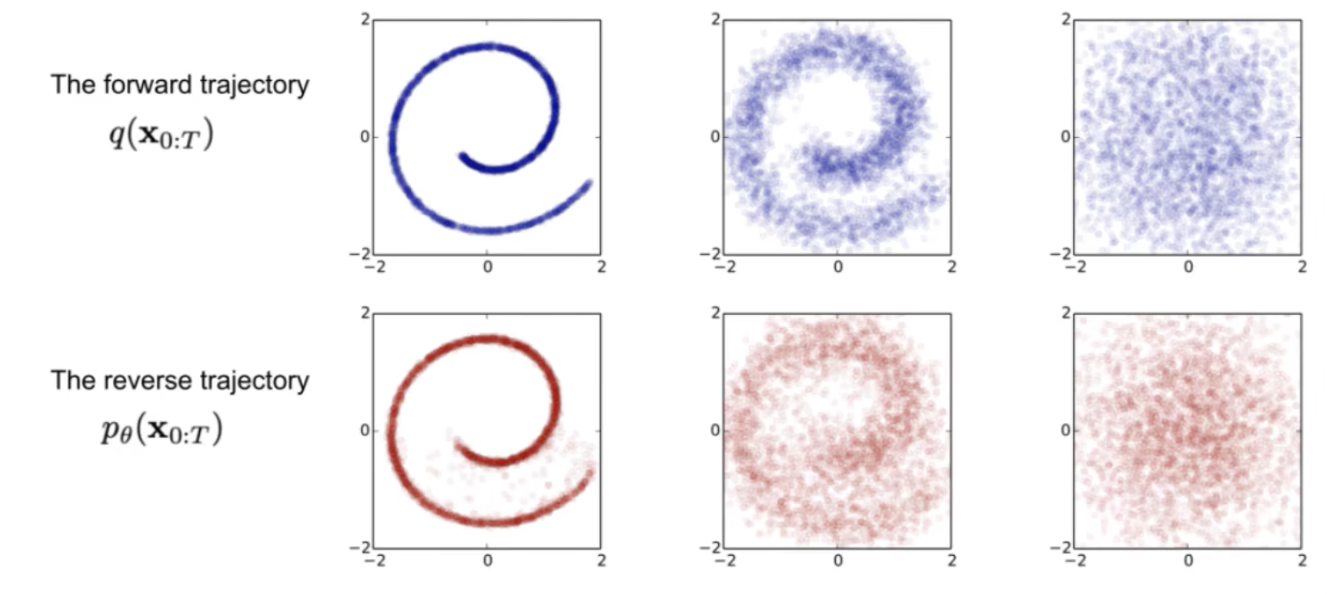
image-20221020121321481
  • Q：x0x_0能不通过递归直接变成xtx_t，那xtx_t能直接变成x0x_0吗？
  • A：不行，公式上推导不出来，需要迭代

（化简过程需要 贝叶斯公式。另外说一下，原始论文的推导不是用贝叶斯公式开始的，是从概率论角度说的，难度可能会更大一点）

q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0) 化简思路：使用贝叶斯公式∼N (均值μ, 方差σ2)q(xt−1∣x0)=aˉt−1x0+1−aˉt−1z∼N (aˉt−1x0, 1−aˉt−1)q(xt∣x0)=aˉtx0+1−aˉtz∼N (aˉtx0, 1−aˉt)q(xt−1∣xt,x0)=aˉtxt−1+1−aˉtz∼N (aˉtxt−1, 1−aˉt) q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\\~\\ 化简思路：使用贝叶斯公式\\ \begin{aligned} &&& \sim N~(均值\mu,~方差\sigma^2)\\ q(x_{t-1}|x_0) =& \sqrt{\bar a_{t-1}}x_0 + \sqrt{1-\bar a_{t-1}}z && \sim N~(\sqrt{\bar a_{t-1}}x_0,~1-\bar a_{t-1}) \\ q(x_{t }|x_0) =& \sqrt{\bar a_{t}}x_0 + \sqrt{1-\bar a_{t}}z && \sim N~(\sqrt{\bar a_{t}}x_0,~1-\bar a_{t}) \\ q(x_{t-1}|x_t,x_0) =& \sqrt{\bar a_{t}}x_{t-1} + \sqrt{1-\bar a_{t}}z && \sim N~(\sqrt{\bar a_{t}}x_{t-1},~1-\bar a_{t}) \\ \end{aligned}\\~\\

化简过程

这三项都通过前向过程能算出来，分布也列出来了∝exp⁡(−12((xt−atxt−1)2βt+(xt−1−aˉt−1x0)21−aˉt−1+(xt−aˉtx0)21−aˉt))因为exp⁡运算。把标准正态分布展开后，乘法就相当于加，除法就相当于减，把他们汇总  展开∝ exp⁡(−12((xt−atxt−1)2βt+(xt−1−aˉt−1x0)21−aˉt−1+(xt−aˉtx0)21−aˉt))= exp⁡(−12(……))，拆开平方= exp⁡(−12((atβt+11−aˉtt−1)xt−12−(2atβtxt+2aˉt−11−aˉt−1x0)xt−1+C(xt,x0)))  C是常数项。这个任务中，核心就是求跟Xt−1有关的，其他的都不关心。展开是为了给xt−1配方exp⁡(−(x−μ)22σ2)= exp⁡(−12(1σ2x2−2μσ2x+μ2σ2))，这样能得到均值和方差所以μ~t(xt,x0)= at(1−aˉt−1)1−aˉtxt+aˉt−1βt1−aˉtx0，配完化简的结果又xo= 1aˉt(xt−1−aˉtzt)，之前是已知x0求xt，这条公式逆了一下这三项都通过前向过程能算出来，分布也列出来了\\ \propto \exp\left(-\frac12\left( \frac{(x_t-\sqrt{a_t}x_{t-1})^2}{\beta_t}+ \frac{(x_{t-1}-\sqrt{\bar a_{t-1}}x_{0})^2}{1-\bar a_{t-1}}+ \frac{(x_t-\sqrt{\bar a_t}x_{0})^2}{1-\bar a_t} \right)\right)\\ 因为\exp运算。把标准正态分布展开后，乘法就相当于加，除法就相当于减，把他们汇总\\~\\~\\ \begin{aligned} 展开\propto~& \exp\left(-\frac12\left( \frac{(x_t-\sqrt{a_t}x_{t-1})^2}{\beta_t}+ \frac{(x_{t-1}-\sqrt{\bar a_{t-1}}x_{0})^2}{1-\bar a_{t-1}}+ \frac{(x_t-\sqrt{\bar a_t}x_{0})^2}{1-\bar a_t} \right)\right)\\ =~& \exp\left(-\frac12\left(……\right)\right)，拆开平方\\ =~& \exp\left(-\frac12\left( {\color{red}(\frac{a_t}{\beta_t}+\frac1{1-\bar a_t{t-1}})x^2_{t-1}}- {\color{cyan}(\frac{2\sqrt a_t}{\beta_t}x_t+\frac{2\sqrt{\bar a_{t-1}}}{1-\bar a_{t-1}}x_0)x_{t-1}}+ C(x_t,x_0) \right)\right)\\~\\~\\ & C是常数项。这个任务中，核心就是求跟X_{t-1}有关的，其他的都不关心。展开是为了给x_{t-1}配方\\ \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) =~& \exp\left(-\frac12\left( \frac 1{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2} \right)\right)，这样能得到均值和方差\\ 所以\tilde\mu_t(x_t,x_0) =~& \frac{\sqrt{a_t}(1-\bar a_{t-1})}{1-\bar a_t}x_t + \frac{\sqrt{\bar a_{t-1}\beta_t}}{1-\bar a_t}x_0，配完化简的结果\\ 又x_o =~& \frac1{\sqrt{\bar a_t}}(x_t-\sqrt{1-\bar a_t}z_t)，之前是已知x_0求x_t，这条公式逆了一下 \end{aligned}\\

得到最终结果

μ~t=1at(xt−βt1−aˉtzˉt)\tilde\mu_t = \frac1{\sqrt{a_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar a_t}}\bar z_t)

其中，ZtZ_t是什么？ZtZ_t是我们估计的每个时刻的噪声

  • 这东西看起来无法直接求解，只能训练一个模型来计算
  • 这些相关论文里竟然都用Unet这种结构来玩的，可能是编码和解码看着比较舒服
  • 模型的输入参数有两个，分别是当前时刻的分布和时刻t

汇总两个阶段

把两个阶段汇总到一起，就是终极流程图了

image-20221021060057809

代码

import math
from inspect import isfunction
from funtools import partial

%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
from einops import rearrange

import torch
from torch import nn, einsum
import torch.nn.functional as F

辅助函数

def exists(x):
    return x is not None

def default(val, d):
    if exists(val):
        return val
    return d() if isfunction(d) else d 

class Residual(nn.Module):
    ……
……
链接到当前文件 0
没有文件链接到当前文件