吴恩达深度学习
目录
优化算法
小笔记(群里讨论时记的):优化么,洗数据,特征工程,bad case分析,换更大模型,增强模型内参数传播
小批量梯度下降(Mini-batch gradient descent)
Mini-batch 梯度下降
向量化超大样本 的缺点
之前学过,向量化能够让你有效地对所有m个样本进行计算,我们要把训练样本放大巨大的矩阵当中:
X=[x(1) x(2) x(3)……x(m)],X的维数是(nx,m),
Y=[y(1) y(2) y(3)……y(m)],Y的维数是(1,m),
向量化能够让你相对较快地处理所有m个样本。但如果m很大的话,处理速度仍然缓慢
原理
如果m是500万或5000万或者更大的一个数,在对整个训练集执行梯度下降法时。
你必须处理整个训练集的500万个训练样本,进行一步梯度下降法,然后要再重新处理500万个训练样本,进行下一步梯度下降法。
如果你在处理完整个500万个样本的训练集之前,先让梯度下降法处理一部分,你的算法速度会更快,这就是Mini-batch梯度下降的思想
新的术语
mini-batch:
把训练集分割为小一点的子集训练,这些子集被取名为mini-batch。
假设每一个子集中只有1000个样本,那么把其中的x(1)到x(1000)取出来,将其称为第一个子训练集,也叫做mini-batch,
然后你再取出接下来的1000个样本,从x(1001)到x(2000),然后再取1000个样本,以此类推。
大括号 { }:
接下来我要说一个新的符号,把x(1)到x(1000)称为X{1},x(1001)到x(2000)称为X{2},
如果你的训练样本一共有500万个,每个mini-batch都有1000个样本,那么共有5000个mini-batch,最后得到是X{5000}。对Y也要进行相同处理
X{t}和Y{t}的维数:
如果X{1}是一个有1000个样本的训练集,所有的子集X{t}维数都是(nx,1000),Y{t}的维数都是(1,1000)
一代:
遍历完整个(X,Y),也可被称为进行 “一代”(1 epoch)的训练。一代这个词意味着只是一次遍历了训练集。
结合正则化
如果你用到了正则化。这是普通梯度下降法的正则化:
J=10001∑i=1lL(y^(i),y(i))+21000λ∑l∣∣w[l]∣∣F2
这是mini-batch梯度下降法中的表示:
J{t}=10001∑i=1lL(y^(i),y(i))+21000λ∑l∣∣w[l]∣∣F2
比较
名称
速度
一些补充:
如果你有一个非常大的训练集,mini-batch梯度下降法比batch梯度下降法运行地更快。几乎每个研习深度学习的人在训练巨大的数据集时都会用到
理解mini-batch梯度下降法(Understanding mini-batch gradient descent)
看下面的三种情况:
- 极端情况 - mini-batch的大小等于m,其实就是batch梯度下降法
- 极端情况 - mini-batch的大小等于1,该新的算法叫随机梯度下降法。每个样本都是独立的mini-batch
- 正常情况 - mini-batch的大小适中,即为正常的min-batch梯度下降法
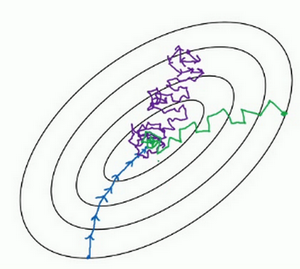
(图中:蓝线为batch梯度下降法、紫线为随机梯度下降法,绿线为min-batch梯度下降法)
分析:
batch梯度下降法:噪声低,步进幅度大,可以收敛
随机梯度下降法:噪声很大,需要更小的学习率降噪。
- 缺点1:它最终会靠近最小值,不过有时候也会方向错误。并且永远不会收敛,而是会一直在最小值附近波动
- 缺点2:失去了向量化的加速
mini-batch下降法:mini-batch大小应该1和m之间
大小较大时,下降速度越快,但产生的噪声越多。没有每次迭代都下降是不要紧的,但走势应该向下
它比随机梯度下降要更持续地靠近最小值的方向,但它也不一定在很小的范围内收敛或者波动。解决方法是结合学习率衰减使用
mini-batch大小的选择
- 如果训练集较小,直接使用batch梯度下降法
- 这里的少是说小于2000个样本,必要使用mini-batch梯度下降法
- 样本数目较大的话,一般的mini-batch大小为64到512
- 考虑到电脑内存设置和使用的方式,如果mini-batch大小是2的n次方,代码会运行地快一些。一般是64~512,也有1024但比较少见
- (这条我没懂)最后需要注意mini-batch中,要确保X{t}和Y{t}要符合CPU/GPU内存,取决于你的应用方向以及训练集的大小
- 多尝试几个值,试图找到一个高效的方案
mini-batch梯度下降,令算法运行得更快,特别是在训练样本数目较大的情况下。
不过还有个更高效的算法,比梯度下降法和mini-batch梯度下降法都要高效的多,后面再讲解。(看目录应该是 “动量梯度下降法”)
Momentum(动量梯度下降法)
原标题:动量梯度下降法(Gradient descent with Momentum)
【前置知识】指数加权平均数(Exponentially weighted averages)
我想向你展示几个优化算法,它们比梯度下降法快,
但要理解这些算法,你需要用到指数加权平均,在统计中也叫做指数加权移动平均,我们首先讲这个,然后再来讲更复杂的优化算法。
它在统计学中被称为指数加权移动平均值,我们就简称为指数加权平均数(好像有时你也会简称为移动平均值)
- “移动” 可以理解为使用了该算法后曲线会右移。当β参数进一步增大、平均更多的天数时,右移程度会更大
- “平均” 可以理解为该算法降噪了,有点像将几天((1−β)1)平均成一天来看的感觉
- “指数” 应该指的是将迭代式全部展开的式子,比如第一天的数据会一直影响后面的数据到最后一天(当然影响会越来越小)
- “加权” 这个简单,不解释
数据图
下图是一年的 天气-温度 图,起始于1月份,结束于12月末
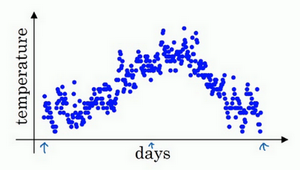
指数加权平均值
操作:
先令v0=0vt=0.9vt−1+0.1θt 通俗理解就是:每天用0.9加权之前的数值加上当日温度的0.1倍,某天的v等于前一天v值的0.9加上当日温度的0.1 我们把0.9这个常数变成β,将之前的0.1变成(1−β)vt=βvt−1+(1−β)θt
举例:
- 第一天:v1=0.9v0+0.1θ1,所以这里是第一天的温度值。
- 第二天:v2=0.9v1+0.1θ2,以此类推。
- 第三天:v3=0.9v2+0.1θ3,如此往下。
代码表示:
v = 0
for i:
get theta_t
v = beta*v + (1-beta)*theta_t
图像:
如此计算,用红线作图的话,得到下图:
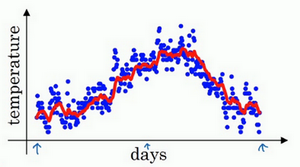
平均温度:
在计算时可视vt大概是(1−β)1的每日温度。
如果β是0.9,这是十天的平均值,也就是红线
将β设置为接近1的一个值,比如0.98,计算(1−0.98)1=50,也就是绿线的部分
β的选值
| β的值 | 线色 | 图像 | 平均几天 |
|---|
| β=0.9 | 红线 |  | 10天 |
| β=0.95 | 绿线 | 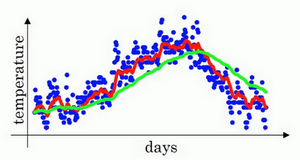 | 50天 |
| β=0.5 | 黄线 | 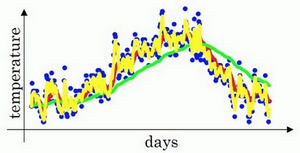 | 2天 |
β较大时
β较小时
选用
- 通过调整β参数,或者说后面的算法学习,你会发现这是一个很重要的参数,可以取得稍微不同的效果。
往往中间有某个值效果最好,β为中间值时得到的红色曲线,比起绿线和黄线更好地平均了温度。
【前置知识】指数加权平均数 - 深入理解
指数加权平均数的关键方程:vt=βvt−1+(1−β)θt
β=0.90时,结果是红线,
β=0.98时,结果是绿线,
β=0.50时,结果是黄线。

每日温度的平均值:
我们进一步地分析,来理解如何计算出每日温度的平均值。
t从0到1到2到3,t的值在不断增加。但为了更好地分析,反过来写,使t的值不断减小
v100=0.9v99+0.1θ100v99=0.9v98+0.1θ99v98=0.9v97+0.1θ98⋯
以此类推,如果你把这些括号都展开:
v100==+++++ 0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+0.1×(0.9)4θ96+… 0.1×θ100 0.1×0.9 θ99 0.1×(0.9)2θ98 0.1×(0.9)3θ97 0.1×(0.9)4θ96 …
这些系数(0.1, 0.1×0.9, 0.1×(0.9)2, 0.1×(0.9)3…),相加起来为1或者逼近1,我们称之为偏差修正,下一节会涉及
到底需要平均多少天的温度?(这里我不是很懂,平均温度用来干嘛,为什么需要计算平均温度?)
(1−ε)(ε1) 当ε=0.10时:当ε=0.02时:当ε=0.0001时:原式=0.9010≈0.3487≈e1≈0.3679原式=0.9850≈0.3642≈e1≈0.3679原式=0.99990.0001≈0.3679≈e1≈0.3679 这其实是数学里的一个极限:x→∞lim(1+x1)x=e1
我们由此得到公式,我们平均了大约(1−β)1天的温度(这里1−β代替了ε)
也就是说根据一些常数,你能大概知道能够平均多少日的温度,不过这只是思考的大致方向,并不是正式的数学证明。
指数加权平均数公式
- 优点
- 占用极少内存,电脑内存中只占用一行数字而已,基本上只占用一行代码,然后把最新数据代入公式,不断覆盖就可以了
- 缺点
- 如果保存所有最近的温度数据,和过去10天的总和,必须占用更多的内存,执行更加复杂,计算成本也更加高昂
- 当然它并不是最好的,也不是最精准的计算平均数的方法。下一节会使用偏差修正计算更准确的计算方式
【前置知识】指数加权平均数 - 偏差修正(Bias correction)
有一个技术名词叫做偏差修正,可以让平均数运算更加准确
vt=βvt−1+(1−β)θt
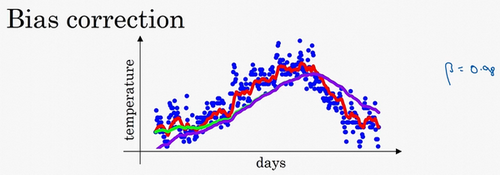
- β=0.90时对应红色曲线,
- β=0.98时理想对应绿色曲线,
- β=0.98时实际对应紫色曲线。紫色曲线相比绿色的起点更低,我们来看看怎么处理
原因:
计算第一天时
v0=0,v1=0.02,v1=0.98v0+0.02θ1=0.02θ1
若θ1=40,原式=0.02×40=0.8。得到的值会小很多,所以第一天温度的估测不准。
计算第二天时
v2=0.98v1+0.02θ2=0.98×0.02θ1+0.02θ2=0.0196θ1+0.02θ2
假设θ1和θ2都是正数,计算后v2要远小于θ1和θ2,所以v2不能很好估测出这一年前两天的温度。
解决方法:
- 有个办法可以修改这一估测,让估测变得更好,更准确,特别是在估测初期,也就是不用vt,而是用1−βtvt,t就是现在的天数。
原公式:vt原=带偏差修正的公式:vt新===βvt−1+(1−β)θt1−βtvt原1−βtβvt−1+(1−β)θt1−βtβvt−1+1−βt(1−β)θt 其中,分母(1−βt)取值(0,1)
举例:
估测第二天温度
原公式,估测值比实际温度低很多:v2=0.0196θ1+0.02θ2 带偏差修正的公式,估测值和实际温度差不多:1−βt=1−0.982=0.0396v2:=0.0396v2=0.4950θ1+0.5051θ2
在后续学习阶段,t很大时βt接近于0,偏差修正几乎没有作用,紫线基本和绿线重合了
在开始学习阶段,偏差修正可以帮助你更好预测温度,可以帮助你使结果从紫线变成绿线
其他补充
在计算指数加权平均数的大部分时候,大家不在乎执行偏差修正,因为大部分人宁愿熬过初始时期,拿到具有偏差的估测,然后继续计算下去。
如果你关心初始时期的偏差,在刚开始计算指数加权移动平均数的时候,偏差修正能帮助你在早期获取更好的估测。
所以你学会了计算指数加权移动平均数,我们接着用它来构建更好的优化算法吧!
动量梯度下降法
还有一种算法叫做Momentum,或者叫做动量梯度下降法。运行速度几乎总是快于标准的梯度下降算法。
简而言之,基本的想法就是计算梯度的指数加权平均数,并利用该梯度更新你的权重
例如,如果你要优化成本函数,函数形状如图,红点代表最小值的位置,假设你从这里(蓝色点)开始梯度下降法,如果进行梯度下降法的一次迭代,无论是batch或mini-batch下降法,也许会指向这里,现在在椭圆的另一边,计算下一步梯度下降,结果或许如此,然后再计算一步,再一步,计算下去,你会发现梯度下降法要很多计算步骤对吧?
这种上下波动减慢了梯度下降法的速度,你就无法使用更大的学习率,如果你要用较大的学习率(紫色箭头),结果可能会偏离函数的范围
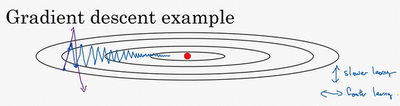
在纵轴上,你希望学习慢一点,因为你不想要这些摆动。
在横轴上,你希望加快学习,你希望快速从左向右移,移向最小值,移向红点。
动量梯度下降法
之前计算移动平均数的公式:v=βv+(1−β)θt 类似的,我们可以在梯度下降时进行降噪:vdW=vdb= W:=b:=βvdW+(1−β)dWβvdb+(1−β)dbW−a⋅vdWb −a⋅vdb
补充
vdW初始值是0,和dW拥有相同维数的零矩阵,也就是跟W拥有相同的维数。
vdb初始值也是向量零,和db拥有相同的维数,也就是和b是同一维数。
在梯度下降中不需要考虑偏差修正
一些理解思路
降噪理解:
指数加权平均数,能起到类似于降噪整流的功能。而用在梯度下降中,能降低梯度下降方向的噪点,使下降方向更平滑
算法走了一条更加直接的路径,在抵达最小值的路上减少了摆动
球的滚动:
想象你有一个碗,你拿一个球,微分项给了这个球一个加速度,此时球正向山下滚,球因为加速度越滚越快,而因为β 稍小于1,表现出一些摩擦力,所以球不会无限加速下去,所以不像梯度下降法,每一步都独立于之前的步骤,你的球可以向下滚,获得动量,可以从碗向下加速获得动量。
两个超参数
所以你有两个超参数,学习率a以及参数β
β控制着指数加权平均数。β最常用的值是0.9
我们之前平均了过去十天的温度,所以现在平均了前十次迭代的梯度。你可以尝试不同的值,可以做一些超参数的研究,不过0.9是很棒的鲁棒数。
不需要考虑偏差修正。你可以拿vdW和vdb除以1−βt,但实际上人们不这么做
因为10次迭代之后,因为你的移动平均已经过了初始阶段。实际中使用梯度下降法或动量梯度下降法时,人们不会受到偏差修正的困扰
公式的第二种写法
最后要说一点,如果你查阅了动量梯度下降法相关资料,你经常会看到不是vdW=βvdW+(1−β)dW而是vdW=βvdW+dW
这两种写法都可以。但使用第二种写法时,vdW缩小了1−β倍,所以你要用梯度下降最新值的话,a要根据1−β1相应变化
我(“我” 指吴恩达老师)认为第二种用起来没有那么自然,因为如果你要调整超参数β,就会影响到vdW和vdb,你也许还要修改学习率a。
所以我更喜欢第一种的公式。
但是两个公式都将β设置为0.9,是超参数的常见选择,只是在这两个公式中,学习率a的调整会有所不同。
RMSprop(均方根传递,Root Mean Square prop)
一些英语:
- 动量(Momentum)
- 均方根、平方平均数(Root Mean Square),Root根 Mean平均 Square平方
- 均方根Prop(RMSprop,Root Mean Square prop),prop暂时不知道怎么翻译
- 均方根误差(Root Mean Square error)
动量(Momentum)可以加快梯度下降,还有一个叫做RMSprop(root mean square prop)的算法,也可以加速梯度下降
算法的名字:RMSprop,全称是均方根Prop 。因为你将微分进行平方,然后最后使用平方根。
作用:
我们之前的例子执行梯度下降时,虽然横轴方向正在推进,但纵轴方向会有大幅度摆动。
假设纵轴代表参数b,横轴代表参数W
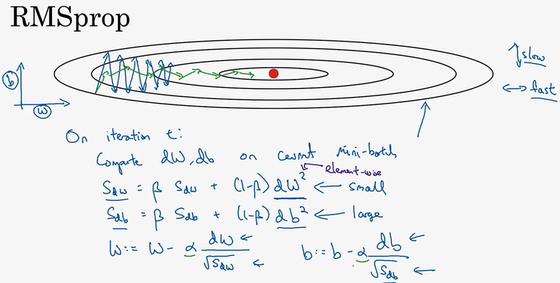
你如果希望减缓b方向(即纵轴方向)的学习,同时加快,至少不是减缓横轴方向的学习。RMSprop算法可以实现这一点(蓝线变绿线)
纵轴方向上摆动较小,而横轴方向继续推进。还有个影响就是,你可以用一个更大学习率a,然后加快学习。
Q:为什么W能表示横轴,b能表示纵轴?
A:看上图中的碗 (凸) 函数的俯视图就知道了。
另外要说明一点,把纵轴和横轴方向分别称为b和W,只是为了方便展示而已。实际中可能会有更高维度的空间
例如,垂直维度的摆动可能是参数W1,W2等的合集。水平维度则可能W3,W4等
实现:
旧方案(普通的梯度下降法)
W:=b:=W−a⋅dWb −a⋅db
旧方案(动量梯度下降法)
vdW=vdb= W:=b:=βvdW+(1−β)dWβvdb+(1−β)dbW−a⋅vdWb −a⋅vdb
新方案(RMSprop)
我们用到新符号SdW,Sdb,而不是vdW,vdb。公式上也多一个平方
SdW=Sdb= W:=b:=β2SdW+(1−β2)dW2β2Sdb +(1−β2)db2W−a⋅SdWdwb −a⋅Sdbdb 注意这个平方的操作是针对这一整个符号的操作,这样做能够保留微分平方的加权平均数即dW2=(dW)2=d(W2)
补充:
下一节中,我们会将RMSprop和Momentum结合起来。
我们在Momentum中采用了超参数β,为了避免混淆,RMSprop中改用超参数β2表示
原理:
在横轴方向 (例子中的W方向) ,我们希望学习速度快,
在垂直方向 (例子中的b 方向) ,我们希望减缓纵轴上的摆动。所以有了SdW和Sdb。
因为dW较小,所以SdW相对较小,最终W方向的更新会较大,
因为db 较小,所以Sdb 相对较大,最终b 方向的更新会较小。
在你要消除摆动的维度中,最终你要计算一个更大的和值,这个平方和微分的加权平均值,所以你最后去掉了那些有摆动的方向。
注意项:
要确保你的算法不会除以0,如果SdW的平方根趋近于0,得到的答案就非常大,不利于确保数值的稳定
解决方案:实际操练时,在分母上加上一个很小很小的ε。ε是多少没关系,10−8是个不错的选择,这只是保证数值能稳定一些,无论什么原因,你都不会除以一个很小很小的数。
小故事:
关于RMSprop的一个有趣的事是,它首次提出并不是在学术研究论文中,而是在多年前Jeff Hinton在Coursera的课程上。
我想Coursera并不是故意打算成为一个传播新兴的学术研究的平台,但是却达到了意想不到的效果。就是从Coursera课程开始,RMSprop开始被人们广为熟知,并且快速发展。
Adam 优化算法(Adam optimization algorithm)
算法的名字:
优点:
很多优化算法被指出不能一般化,而RMSprop以及Adam优化算法是少有的经受住人们考验的两种算法,已被证明适用于不同的深度学习结构
Adam优化算法基本上就是结合了Momentum和RMSprop梯度下降法。一种极其常用的学习算法,被证明能有效适用于不同神经网络,适用于广泛的结构
使用:
Adam算法初始化:vdW=0,SdW=0vdb =0,Sdb =0注意计算dW,db时可以结合mini−batch计算 −−−−−−−−−−−−−−−−−−−−−Momentum法的 指数加权平均数:vdW=vdb =β1vdW+(1−β1)dWβ1vdb +(1−β1)db −−−−−−−−−−−−−−−−−−−−−RMSprop法的 参数:SdW=Sdb =β2SdW+(1−β2)(dW)2β2Sdb +(1−β2)(db )2 −−−−−−−−−−−−−−−−−−−−−Adam算法的时候,还要计算偏差修正:vdWcorrected=vdbcorrected=SdWcorrected=Sdbcorrected=1−β1tvdW1−β1tvdb1−β2tSdW1−β2tSdb −−−−−−−−−−−−−−−−−−−−−梯度下降:W:=b:=W−α⋅SdWcorrected+εvdWcorrectedb −α⋅Sdbcorrected+εvdbcorrected
本算法中有很多超参数:
- a (学习率):很重要,也经常需要调试,你可以尝试一系列值,然后看哪个有效
- β1 (第一矩):常用的缺省值为0.9。这是dW的移动平均数,也就是dW的加权平均数
- β2 (第二矩):Adam论文作者暨算法的发明者,推荐使用0.999。这是在计算(dW)2以及(db)2的移动加权平均值
- ε:其设置其实没那么重要,Adam论文的作者建议ε为10−8。但你并不需要设置它,因为它并不会影响算法表现
- 在使用Adam的时候,人们往往使用缺省值即可,β1,β2和ε都是如此。
我觉得没人会去调整ε,然后尝试不同的a值,看看哪个效果最好。
你也可以调整β1和β2,但我认识的业内人士很少这么干。
学习率衰减(Learning rate decay)
加快学习算法的一个办法就是随时间慢慢减少学习率,我们将之称为学习率衰减
场景:
假设你要使用mini-batch梯度下降法,mini-batch数量不大,大概64或者128个样本,在迭代过程中会有噪音(蓝色线)。
下降朝向这里的最小值,最后在附近摆动,但是不会真正地收敛。因为你用的a是固定值。
解决思路:
慢慢减少学习率a。其本质在于,在学习初期,你能承受较大的步伐,但当开始收敛的时候,小一些的学习率能让你步伐小一些。
结果:蓝线会变成绿线
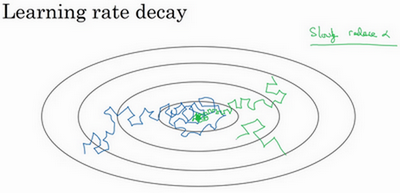
解决方案实现:
你应该拆分成不同的mini-batch,第一次遍历训练集叫做第一代。第二次就是第二代,依此类推。如下设置学习率a
a==1+decay-rate∗epoch-num1a01+衰减率∗代数1初始学习率 其中,除了初始学习率a0,{衰减率}是你需要调整的另一超参数
例如:
如果a0为0.2,衰减率decay-rate为1。
第一代a=1+11a0=0.1,第二代a=0.067,第三代a=0.05,第四代a=0.04,……
你的学习率呈递减趋势。如果你想用学习率衰减,要做的是要去尝试不同的值,包括超参数a0和衰退率
其他学习率衰减公式:
a=1+decay-rate∗epoch-num1a0,当前公式
a=0.95epoch-numa0,指数衰减,学习率呈指数下降
a=epoch-numka0
a=tka0(t为mini-batch的数字)。
有时人们也会用一个离散下降(discrete stair cease)的学习率。
也就是某个步骤有某个学习率,一会之后,学习率减少了一半,一会儿减少一半,一会儿又一半
人们有时候还会做一件事,手动衰减。
如果你一次只训练一个模型,如果你要花上数小时或数天来训练,有些人的确会这么做。
看看自己的模型训练,耗上数日,然后他们觉得,学习速率变慢了,我把a调小一点。时复一时,日复一日地手动调整a。
只有模型数量小的时候有用,但有时候人们也会这么做。
现在你有了多个选择来控制学习率a。你可能会想,好多超参数,究竟我应该做哪一个选择。下一章,我们会讲到,如何系统选择超参数。
局部最优的问题(The problem of local optima)
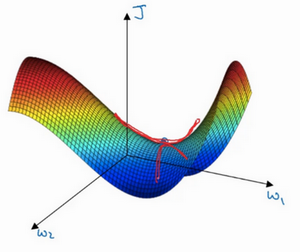
在深度学习研究早期,人们总是担心优化算法会陷入糟糕的局部最优(Local Optima)中,
不过随着深度学习理论不断发展,我们对局部最优的理解也发生了改变。下面介绍一些解决方案
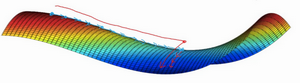
事实上,如果你要创建一个神经网络,通常梯度为零的点并不是这个图中的局部最优点,而是鞍点。
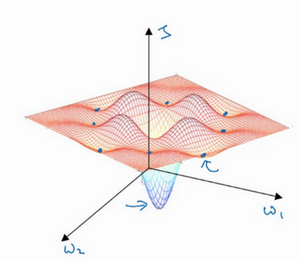
Q:为什么更可能是鞍点而不是局部最优点?
A:一个具有高维度空间的函数,如果梯度为0,那么在每个方向,它可能是凸函数,也可能是凹函数。
如果你在2万维空间中,那么想要得到局部最优,所有的2万个方向都需要是这样,但发生的机率也许很小,也许是2−20000,
你更有可能遇到有些方向的曲线会这样向上弯曲,另一些方向曲线向下弯,而不是所有的都向上弯曲,
因此在高维度空间,你更可能碰到鞍点。就像下面的这种:
所以我们从深度学习历史中学到的一点就是:我们对低维度空间的大部分直觉,比如你可以画出二维或三维的图,并不能应用到高维度空间中
因为如果你有2万个参数,那么J函数有2万个维度向量,你更可能遇到鞍点,而不是局部最优点。
- Q:为什么叫做鞍点?
- A:因为长得就是放在马背上的马鞍一样。比如双曲抛物面也叫马鞍面
总结要点:
- 首先,你不太可能困在极差的局部最优中(前提是你在训练较大的神经网络,存在大量参数,并且成本函数J被定义在较高的维度空间)
- 其次,平稳段是一个问题,这样使得学习十分缓慢。
像Momentum、RMSprop、Adam这样的算法,能够加快学习速度,让你尽早往下走出平稳段。