吴恩达深度学习

目录

超参数调试、Batch正则化和程序框架

超参数调试

参数调试过程（Tuning process）

不同超参数的重要程度：
（事实证实一些超参数比其它的更为重要）

超参数	名称	重要程度	补充
$\alpha$	学习率	最重要
$\beta~(\beta_1，\beta_2，\varepsilon)$	Adam算法参数	第二重要	事实上，我从不调试$\beta_{1}$，${\beta}_{2}$和$\varepsilon$，如果你想的话也可以调试它们 总是选定其分别为0.9，0.999和$10^{-8}$
$\text{Layers}$	神经网络层数	第三重要
$\text{Hidden~units}$	神经网络层的单元数	第二重要
$\text{Learning rate decay}$	学习率衰减	第三重要
$\text{Mini-batch~size}$	mini-batch算法的batch大小	第二重要

如何选择调试值

接下来介绍三种方法

• 充分搜索（Adequate search）
• 随机取样（Random sampling）
• 从粗到精搜索（随机 + Coarse to fine search）

【方法一】早一代的机器学习算法的做法

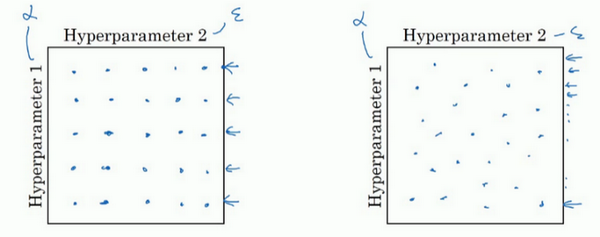
如果你有两个超参数，这里我会称之为超参1，超参2。常见的做法是在网格中取样点，像下图的左侧那样，

这里我放置的是5×5的网格，网格数量也可多可少。

对于这个例子，你可以尝试这所有的25个点，然后选择哪个参数效果最好。当参数的数量相对较少时，这个方法很实用。

【方法二】现在常用的方法

深度学习中随机选择点。比如还是选择25个点，像下图右侧那样，然后用这些随机取的点试验超参数的效果

比较这两种做法

• 举一个极端的例子：假设超参数1是$a$（学习速率），超参数2是Adam算法中分母中的$\varepsilon$
  在这种情况下，$a$的取值很重要，而$\varepsilon$取值则无关紧要。

• 方法一：
  因为$a$值只有5个，最后得到的25种模型里，实际上基本属于5种

• 方法二：
  使用随机取值，25个取样点的$a$值基本都是离散的，最后会产生25种差距比较大的模型

如何选择调试值 - 多参数

实践中，的超参数可能不止两个。但基本都是同理的

例如：你有三个超参数，这时你搜索的不是一个方格，而是一个立方体，超参数3代表第三维

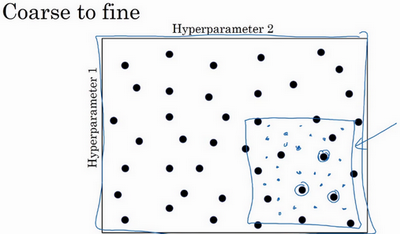
【方法三】区域定位的抽样方案，由粗糙到精细的策略

比如在二维的那个例子中，也许你会发现效果最好的某个区域，那在接下来要做的是放大这块小区域（小蓝色方框内），

然后在其中更密集得取值或随机取值，聚集更多的资源，在这个蓝色的方格中搜索。

为超参数选择合适的范围（Using an appropriate scale to pick hyperparameters）

随机取值可以提升你的搜索效率。但随机取值并不是在有效范围内的随机均匀抽样（sampleing uniformly at random），而是选择合适的标尺（scale）

• 举例一

  • 你要选取隐藏层单元的数量$n^{[l]}$，假设取值范围是$50\sim 100$。

  • 此时，你可以从一条$50\sim 100$的数轴上随机取点

• 举例二

  • 你要选取神经网络的层数$L$，假设选择层数的范围是$2\sim4$。

  • 那么2，3，4随机均匀取样才比较合理

• 举例三

  • 你要选取超参数$a$（学习率），假设选择的值的范围是$0.0001\sim1$。

  • 此时使用随机均匀取值并不好，用对数标尺会更合理，使用对数轴而非线性轴。在对数轴上均匀随机取点，依次取0.0001，0.001，0.01，0.1，1
    具体代码实现见后面

• 举例四

  • 你要选取超参数$\beta$ 用于计算指数的加权平均值，假设你认为$\beta$是$0.9\sim0.999$的某个值。

  • 解决方案：探究$1-\beta$（公式中含有$\frac{1}{1- \beta}$），值在0.1到0.001区间内。你要做的就是在$[-3,-1]$里随机均匀的给r取值。你设定了$1- \beta = 10^{r}$
    接下来的步骤同例子三

代码实现对数轴上均匀随机取点：（Python）

• 首先r=-4*np.random.rand()。那么$r \in [ 4,0]$，r是该范围内的随机取样
• 然后$ a =10^{r}$。那么$a \in[10^{-4},10]$，$\alpha$是该范围内使用对数标尺的随机取样

超参数调试的实践：熊猫vs鱼子酱（Hyperparameters tuning in practice: Pandas vs. Caviar）

超参数的调试值会经常变的

即使你只研究一个问题，比如说逻辑学，你也许已经找到一组很好的参数设置。但或许在几个月的过程中，观察到你的数据会逐渐改变
或许只是在你的数据中心更新了服务器等原因。正因为有了这些变化，你原来的超参数的设定不再好用

所以我建议，或许只是重新测试或评估你的超参数，至少每隔几个月一次，以确保你对数值依然很满意

关于如何搜索超参数的问题，我见过大概两种重要的思想流派

• 熊猫方式
• 鱼子酱方式

方法一

照看一个模型

前提：通常是有庞大的数据组，但没有许多计算资源或足够的CPU和GPU的前提下。
基本而言，你只可以一次负担起试验一个模型或一小批模型，在这种情况下，即使当它在试验时，你也可以逐渐改良。

比如：
第0天，你将随机参数初始化，然后开始试验，然后你逐渐观察自己的学习曲线，也许是损失函数$J$，或者数据设置误差或其它的东西，
在第1天内逐渐减少，那这一天末的时候，你可能会说，看，它学习得真不错。我试着增加一点学习速率，看看它会怎样，也许结果证明它做得更好，那是你第二天的表现。
两天后，你会说，它依旧做得不错，也许我现在可以填充下Momentum或减少变量。
然后进入第三天，每天，你都会观察它，不断调整你的参数。也许有一天，你会发现你的学习率太大了，所以你可能又回归之前的模型，

像这样，但你可以说是在每天花时间照看此模型，即使是它在许多天或许多星期的试验过程中。所以这是一个人们照料一个模型的方法，观察它的表现，耐心地调试学习率。

但那通常是因为你没有足够的计算能力，不能在同一时间试验大量模型时才采取的办法。

方法二

同时试验多种模型

你设置了一些超参数，尽管让它自己运行，或者是一天甚至多天，然后你会获得像这样的学习曲线，这可以是损失函数J或实验误差或损失或数据误差的损失，但都是你曲线轨迹的度量。

同时你可以开始一个有着不同超参数设定的不同模型，所以，你的第二个模型会生成一个不同的学习曲线，也许是像这样的一条（紫色曲线），我会说这条看起来更好些。
与此同时，你可以试验第三种模型，其可能产生一条像这样的学习曲线（红色曲线），还有另一条（绿色曲线），也许这条有所偏离，像这样，等等。

或者你可以同时平行试验许多不同的模型，橙色的线就是不同的模型。用这种方式你可以试验许多不同的参数设定，然后只是最后快速选择工作效果最好的那个。在这个例子中，也许这条看起来是最好的（下方绿色曲线）。

一个生动的比喻

左边的方法称之为熊猫方式。
当熊猫有了孩子，他们的孩子非常少，一次通常只有一个，然后他们花费很多精力抚养熊猫宝宝以确保其能成活，所以，这的确是一种照料，一种模型类似于一只熊猫宝宝。

右边的方式称之为鱼子酱方式，更像鱼类的行为。
在交配季节，有些鱼类会产下一亿颗卵，但鱼类繁殖的方式是，它们会产生很多卵，但不对其中任何一个多加照料，只是希望其中一个，或其中一群，能够表现出色。

选用

所以这两种方式的选择，是由你拥有的计算资源决定的

• 如果你拥有足够的计算机去平行试验许多模型，那绝对采用鱼子酱方式，尝试许多不同的超参数，看效果怎么样。
• 但在一些应用领域，比如在线广告设置和计算机视觉应用领域，那里的数据太多了，你需要试验大量的模型，所以同时试验大量的模型是很困难的

Batch Norm

归一化网络中的激活函数（Normalizing activations in a network）

在深度学习兴起后，最重要的一个思想是它的一种算法，叫做 Batch Norm（Batch归一化 / 批量归一化），简称BN

• 由来

  由Sergey loffe和Christian Szegedy两位研究者创造

• 作用

  Batch归一化会使你的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，超参数的选择不再那么敏感。从而使你的训练更加容易，深层网络上也表现得很好

归一化输入特征

复习一下归一化输入特征

比如训练logistic回归时，归一化输入特征可以加快学习过程

操作上简单来说就是：计算均值和方差，减去均值，再除以方差。

$$写法一：\\ \begin{aligned} 平均值，\mu=& \frac 1m\sum_i x^{(i)}\\ x^{(i)}:=& x^{(i)}-\mu\\ 方差，\sigma^2=& \frac1m\sum_i {x^{(i)}}^2\\ x^{(i)}:=& \frac {x^{(i)}}{\sigma^2} \end{aligned}\\~\\ 写法二：\\ \begin{aligned} 平均值，\mu=& \frac 1m\sum_i x^{(i)}\\ 方差，\sigma^2=& \frac1m\sum_i {(x^{(i)}-\mu)}^2\\ x^{(i)}:=& \frac {x^{(i)}-\mu}{\sigma^2} \end{aligned}$$

你计算了平均值，从训练集中减去平均值，计算了方差，接着根据方差归一化你的数据集。这可以把价值函数的碗函数，从扁长变得更圆，更易于算法优化。

归一化隐藏层

那么更深的模型呢？对任何一个隐藏层而言，我们能否归一化$a$值。
比如说$a^{[2]}$，是下一层的输入值，进行归一化能以更快的速度训练$w^{[3]}$，$b^{[3]}$。
——这就是Batch归一化的作用

不过严格来说，我们真正归一化的不是$a^{[2]}$，而是$z^{[2]}$。

深度学习文献中有一些争论：在激活函数之前是否应该将值$z^{[2]}$归一化，或是否应该在应用激活函数$a^{[2]}$后再规范值
实践中，经常做的是归一化$z^{[2]}$，这也是吴恩达老师介绍的版本，推荐其为默认选择

Batch归一化的实现

假设你有一些隐藏单元值，$z^{[l](i)}=z^{(1)},\cdots,z^{(m)}$。为了简化符号，这里省略$l$及方括号。进行归一化：
（为了使数值稳定，通常将$\varepsilon$加入分母，以防$σ=0$的情况）

$$\begin{aligned} (1)&& \mu=& \frac 1m\sum_i z^{(i)}\\ (2)&& \sigma^2=& \frac1m\sum_i {(z^{(i)}-\mu)}^2\\ (3)&& z_{norm}^{(i)}=& \frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\varepsilon}}\\ (4)&& {\tilde{z}}^{(i)}=& \gamma z_{\text{norm}}^{(i)} +\beta\\~\\ \end{aligned}$$

前三条公式把这些$z$值归一化，$z$的每一个分量都是平均值0和方差1。

后面多了第四条公式，用来调整${\tilde{z}}^{(i)}$ 均值和方差，因为我们不想让隐藏单元总是含有平均值0和方差1。其中$\gamma$和$\beta$是你模型的学习参数

$\gamma$和$\beta$

• 作用

  你可以随意设置${\tilde{z}}^{(i)}$的平均值，造含其它平均值和方差的隐藏单元值

• 特别地

  $$\begin{aligned} \because~& {\tilde{z}}^{(i)}=\gamma z_{\text{norm}}^{(i)} +\beta， z_{norm}^{(i)}=\frac{z^{(i)} -\mu}{\sqrt{\sigma^{2} +\varepsilon}}\\ \therefore~& {\tilde{z}}^{(i)}=\gamma\frac{z^{(i)} -\mu}{\sqrt{\sigma^{2} +\varepsilon}}+\beta\\~\\ 如果~& \gamma= \sqrt{\sigma^{2} +\varepsilon}，\beta=\mu\\ 那么~& {\tilde{z}}^{(i)} = z^{(i)} \end{aligned}$$

• 应用场景

  为什么需要修改隐藏层的均值和方差？

  

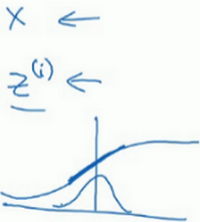
  比如，使用sigmoid激活函数时，你不想让你的值总是全部集中在这里（粗线处）。你想使它们有更大的方差，或想平均值不为0，以便更好的利用非线性的sigmoid函数，这时就可以使用Batch归一化

总结

归一化输入特征$X$是怎样有助于神经网络中的学习，
Batch归一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏层。

你应用Batch归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是：你也许不想隐藏单元值必须是平均值0和方差1。

神经网络中使用 Batch Norm

原标题：将 Batch Norm 拟合进神经网络（Fitting Batch Norm into a neural network）

上一节学习了在单一隐藏层进行Batch归一化，接下来学习它怎样在深度网络训练中使用

神经网络上使用Batch Norm

假设你有一个这样的神经网络

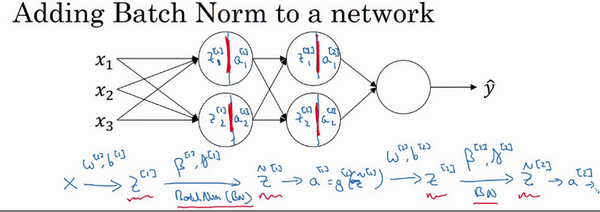
不使用BN的话每个圆圈代表着两步的计算过程，使用BN则是三步

第一层的操作：

• 首先，把输入$X$拟合到第一隐藏层，计算得到$z^{[1]}$，此过程由$w^{[1]}$和$b^{[1]}$两参数控制
• 接着，Batch归一化将$z^{[1]}$值进行Batch归一化，计算得到${\tilde{z}}^{[1]}$，此过程由${\beta}^{[1]}$和$\gamma^{[1]}$两参数控制
• 最后，将其输入激活函数，计算得到$a^{[1]}$，即$a^{[1]} = g^{[1]}({\tilde{z}}^{[ l]})$

第二层的操作：（与第一层类似）

• 首先，计算得到$z^{[2]}$
• 接着，将$z^{[2]}$进行Batch归一化，计算得到${\tilde{z}}^{[2]}$，此过程由${\beta}^{[2]}$和$\gamma^{[2]}$两参数控制
• 最后，通过激活函数计算出$a^{[2]}$

总操作流：

代码实现

代码实现中不太需要考虑那么多细节，一般只要短短的一行代码。

在TensorFlow框架中，你可以用这个函数（tf.nn.batch_normalization）来实现Batch归一化

参数的补充

各个参数的维数：

• $z^{[l]}$的维数是$(n^{[l]},1)$
• $b^{[l]}$的尺寸为$(n^{[l]},1)$
• ${\beta}^{[l]}$和$\gamma^{[l]}$的维度也是$(n^{[l]},1)$

$b^{[l]}$参数的问题

与没有BN的神经网络相比，除了参数$w^{[1]},b^{[1]},\cdots,w^{[l]},b^{[l]}$，还多了另一些参数：${\beta}^{[1]},\gamma^{[1]},\cdots,{\beta}^{[l]},\gamma^{[l]}$

另外，由于$z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$，又因为使用Batch归一化后均值会被重新设置，
所以使用Batch归一化时参数$b^{[l]}$通常可以不要，或设置为0。
$b^{[l]}$这个参数没有意义，功能由${\beta}^{[l]}$代替

从反向传播的角度分析也是如此

区分Batch归一化$\beta^{[l]}$与超参数$\beta$（$\beta_1,\beta_2$）

• Adam论文的作者，在论文里用$\beta$代表超参数。
  用于Momentum或计算各个指数的加权平均值。Momentum、Adam、RMSprop算法中的$\beta$也是如此
• Batch归一化论文的作者，也则使用$\beta$代表此参数（${\beta}^{[1]}$，${\beta}^{[2]}$等等）
• 这是两个完全不同的$\beta$。在两种情况下都决定使用$\beta$，而不是其他符号，以便你阅读那些原创的论文。

结合mini-batch

“Batch Norm” 和 “Mini-Batch梯度下降”，都有 “Batch” 这个词，翻译过来的话分别是 “批量归一化” 和 “小批量梯度下降”，没什么关联。

不过实践中，Batch归一化通常和训练集的mini-batch一起使用。当然也适用于有Momentum、RMSprop、Adam的梯度下降法。

具体步骤：

• 首先使用第一个mini-batch ($X^{\{1\}}$)
  用参数$w^{[1]}$和$b^{[1]}$计算$z^{[1]}$，然后用$w^{[2]}$和$b^{[2]}$计算$z^{[2]}$，等等。最后在第一个mini-batch ($X^{\{1\}}$)上进行一步梯度下降法。
• 第二个mini-batch ($X^{\{2\}}$)、第三个mini-batch ($X^{\{3\}}$) 同理

Batch Norm 为什么奏效？（Why does Batch Norm work?）

为什么Batch归一化会起作用呢？

• 原因一
  • 归一化输入特征值$x$，可以使其均值为0，方差1。通过归一化所有的输入特征值$x$，以获得类似范围的值，加速学习
  • Batch归一化起也在做类似的工作，但不仅仅对于这里的输入值，还有隐藏单元的值
• 原因二
  • 它可以使权重比你的网络更滞后或更深层
  • 比如，第10层的权重更能经受得住变化
• 原因三
  • 有轻微的正则化效果

Covariate shift (协变量转变)

重点解释一下原因二。这属于 Covariate shift (协变量转变) 问题，Batch归一化可以很好地解决 Covariate shift 问题

举个形象点的例子：

这是猫脸识别检测。假设你已经在所有黑猫的图像上训练了数据集，如果现在你要把此网络应用于有色猫，那么你的cosfa可能适用的不会很好

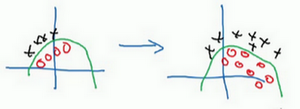
用函数图来举例：

如果你的训练集是下图中左侧部分，你的正面例子为图像红圈，反面例子为黑圈。

你不能去期待：在左边训练得很好的模型，同样在右边也运行得很好。
即使真的存在一个函数可以在两边都很好地运行，但如果只看左边数据的话，学习算法没有办法去发现绿色的决策边界

假设你已经学习了$x$到$y$的映射，如果$x$的分布改变了，那么你可能需要重新训练你的学习算法

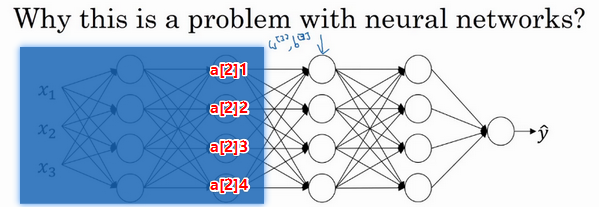
这个问题也适用于神经网络中：

我们从第三层来看学习过程。第三层在训练过程已经学习了参数$w^{[3]}$和$b^{[3]}$。

遮住左边的部分，将这整个神经网络看成是一个新的 只有两个隐藏层的神经网络
从第三隐藏层的角度来看，它的输入函数是$a_{1}^{[2]},a_{2}^{[2]},a_{3}^{[2]},a_{4}^{[2]}$，第三层隐藏层的工作是找到一种方式，使这些值映射到$\hat y$

现在把左边揭开，这个网络还有前面层的一些参数$w^{[1]},b^{[1]},w^{[2]},b^{[2]}$。如果这些参数改变，$a^{[2]}$的值也会改变。
从第三层隐藏层的角度来看，这些隐藏单元的值在不断地改变，所以它也有了“Covariate shift”的问题

Batch归一化解决 Covariate shift问题

Batch归一化可以确保无论前面的参数怎样变化，即使$z_{1}^{[2]},z_{2}^{[2]}$的值改变，$z_{1}^{[2]},z_{2}^{[2]}$的均值和方差保持不变
Batch归一化减少了输入值改变的问题，使后层的值更稳定。即使输入改变了一些，后层的改变也会更少。
它解耦了前层参数的作用与后层参数的作用之间的耦合。它使得网络每层都可以自己学习，稍稍独立于其它层，有助于加速整个网络的学习

正则化效果

Batch归一化还有一个作用，它有轻微的正则化效果

原因：均值和方差上的噪音

在配合mini-batch计算时，比如Batch为64或128或256或更大时。

因为Batch归一化一次只能处理一个batch数据，它在mini-batch上计算的均值和方差（而不是在整个数据集上），所以均值和方差有一些小的噪声（因为它只是由一小部分数据得出）
（个人笔记：按你这意思，是不是只用mini-batch也有正则化效果啊？）

dropout也会添加噪音

前面我们学过dropout（随机失活，另一种正则化方法）是一种正则化算法
Batch的原理与dropout是相似的，它往每个隐藏层的激活值上增加了噪音。
dropout增加噪音的原因是：它使一个隐藏的单元，以一定的概率乘以0，以一定的概率乘以1，所以你的dropout含几重噪音，因为它乘以0或1。

这种噪音会使模型有轻微的正则化效果：

对比而言，Batch归一化含几重噪音，因为标准偏差的缩放和减去均值带来的额外噪音，即给隐藏单元添加了噪音，这迫使后部单元不过分依赖任何一个隐藏单元。此原理类似于dropout。

Batch归一化有轻微的正则化效果，因为添加的噪音很微小，所以并不是巨大的正则化效果。
你也可以将Batch归一化和dropout一起使用，如果你想得到更强大的正则化效果的话。

较大的mini-batch可以减少这种正则化效果

如果你应用了较大的mini-batch，比如说，你用了512而不是64。通过应用较大的min-batch，你减少了噪音，因此减少了正则化效果。

这是dropout的一个奇怪的性质，就是应用较大的mini-batch可以减少正则化效果

吴恩达老师：

我会把Batch归一化当成一种正则化，因为有时它会对你的算法有额外的期望效应或非期望效应。
但是不要把Batch归一化当作正则化，把它当作将你归一化隐藏单元激活值并加速学习的方式，因为正则化几乎是一个意想不到的副作用

测试时的 Batch Norm（Batch Norm at test time）

测试时与训练时的不同：

Batch归一化将你的数据以mini-batch的形式逐一处理

在训练时，下面是用来执行Batch归一化的等式。调节计算的$\mu$和$\sigma^{2}$是在整个mini-batch上进行计算

$$\begin{aligned} (1)&& \mu=& \frac 1m\sum_i z^{(i)}\\ (2)&& \sigma^2=& \frac1m\sum_i {(z^{(i)}-\mu)}^2\\ (3)&& z_{norm}^{(i)}=& \frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\varepsilon}}\\ (4)&& {\tilde{z}}^{(i)}=& \gamma z_{\text{norm}}^{(i)} +\beta\\~\\ \end{aligned}$$

但在测试时，你可能不能将一个mini-batch中的 64 / 128 / 256 个样本同时处理，你只有一个样本。
一个样本的均值和方差没有意义，因此你需要用其它方式来得到$\mu$和$\sigma^{2}$，需要单独估算$\mu$和$\sigma^{2}$（用一个指数加权平均来估算）。

解决方法：

假设我们在第$l$层，使用mini-batch训练，
训练第2个mini-batch，得到第一个$\mu,\sigma^{2}$值（$\mu^{\left\{1 \right\}[l]},\sigma^{2\left\{1 \right\}[l]}$），
训练第2个mini-batch，得到第二个$\mu,\sigma^{2}$值（$\mu^{\{2\}[l]},\sigma^{2\left\{2 \right\}[l]}$），
训练第3个mini-batch，得到第三个$\mu,\sigma^{2}$值（$\mu^{\left\{3 \right\}[l]},\sigma^{2\left\{3 \right\}[l]}$），
……

正如我们之前用指数加权平均（${{v}_{t}}=\beta {{v}_{t-1}}+(1-\beta ){{\theta }_{t}}$）来计算$\theta_{1}$，$\theta_{2}$，$\theta_{3}$的均值，当时是试着计算当前气温的指数加权平均。
现在我们可以用指数加权平均根据这些$\mu^{\{i\}[l]}$来估计这一隐藏层的$z$的均值$\mu^{[l]}$

最后在测试时，对应这个等式（$z_{\text{norm}}^{(i)} = \frac{z^{(i)} -\mu}{\sqrt{\sigma^{2} +\varepsilon}}$）。
你只需要用你的$z$值来计算$z_{\text{norm}}^{(i)}$，用$\mu$和$\sigma^{2}$的指数加权平均，用你手头的最新数值来做调整，然后你可以用左边我们刚算出来的$z_{\text{norm}}$和你在神经网络训练过程中得到的$\beta$和$\gamma$参数来计算你那个测试样本的$\tilde{z}$值。

总结一下（懒得整理了）

在训练时，$\mu$和$\sigma^{2}$是在整个mini-batch（64或128或其它一定数量的样本）上计算出来的

在测试时，你可能需要逐一处理样本，方法是根据你的训练集估算$\mu$和$\sigma^{2}$。
估算的方式有很多种，理论上你可以在最终的网络中运行整个训练集来得到$\mu$和$\sigma^{2}$，
但在实际操作中，我们通常运用指数加权平均来追踪在训练过程中你看到的$\mu$和$\sigma^{2}$的值。
还可以用指数加权平均，有时也叫做流动平均来粗略估算$\mu$和$\sigma^{2}$，然后在测试中使用$\mu$和$\sigma^{2}$的值来进行你所需要的隐藏单元$z$值的调整。

在实践中，不管你用什么方式估算$\mu$和$\sigma^{2}$，这套过程都是比较稳健的，因此我不太会担心你具体的操作方式，而且如果你使用的是某种深度学习框架，通常会有默认的估算$\mu$和$\sigma^{2}$的方式，应该一样会起到比较好的效果。但在实践中，任何合理的估算你的隐藏单元$z$值的均值和方差的方式，在测试中应该都会有效。

Batch归一化就讲到这里，使用Batch归一化，你能够训练更深的网络，让你的学习算法运行速度更快，在结束这周的课程之前，我还想和你们分享一些关于深度学习框架的想法，让我们在下一段视频中一起讨论这个话题。

程序框架

深度学习编程框架

深度学习框架（Deep Learning frameworks）

你已经差不多从零开始学习了使用Python和NumPy实现深度学习算法。

但你会发现，从零开始全部靠自己实现并不现实
除非应用更复杂的模型（例如卷积神经网络，或者循环神经网络），或者当你开始应用很大的模型

类比一下，我猜你知道如何做矩阵乘法，你还应该知道如何编程实现两个矩阵相乘。
你很可能不想用自己的矩阵乘法函数，而是想要访问一个更高效的数值线性代数库。当然如果你明白两个矩阵是怎么相乘的还是有用的

深度学习框架：

框架	补充
Caffe / Caffe2
CNTK
DL4J
Keras
Lasagne
mxnet
PaddlePaddle
TensorFlow	吴恩达的这个教程所教的
Theano
Torch	现在国内的高校基本都是在用PyTorch

选择深度学习框架
（如果你想看看关于这些框架的优劣之处的讨论，我留给你自己去网上搜索。但我认为很多框架都在很快进步越来越好，因此我就不做强烈推荐了）

• 易于编写程序
• 运行快
• 开放（它不仅需要开源，而且需要良好的管理。即你能否相信这个框架能长时间保持开源，它未来有可能出于某种原因选择停止开源，点名批评Google）

TensorFlow

详见对应笔记