吴恩达深度学习

目录

卷积

计算机视觉（Computer vision）

计算机视觉

欢迎参加这次的卷积神经网络课程，计算机视觉是一个飞速发展的一个领域，这多亏了深度学习。

深度学习之所以让我兴奋有下面两个原因

• ① 计算机视觉的高速发展标志着新型应用产生的可能

  这是几年前，人们所不敢想象的。通过学习使用这些工具，你也许能够创造出新的产品和应用。

• ② 由此衍生出新的神经网络结构与算法，这实际上启发人们去创造出计算机视觉与其他领域的交叉成果

  举个例子，之前我在做语音识别的时候，我经常从计算机视觉领域中寻找灵感，并将其应用于我的文献当中
  所以即使你在计算机视觉方面没有做出成果，我也希望你也可以将所学的知识应用到其他算法和结构。

计算机视觉应用

具体应用举例

• 深度学习与计算机视觉可以帮助汽车，查明周围的行人和汽车，并帮助汽车避开它们
• 还使得人脸识别技术变得更加效率和精准，你们即将能够体验到或早已体验过仅仅通过刷脸就能解锁手机或者门锁
• 你手机上一定有很多分享图片的应用。在上面，你能看到美食，酒店或美丽风景的图片。深度学习技术向你展示最为生动美丽以及与你最为相关的图片
• 机器学习甚至还催生了新的艺术类型

应用分类举例

• 图片分类（或图片识别）

  比如给出这张64×64的图片，让计算机去分辨出这是一只猫

  

• 目标检测

  比如在一个无人驾驶项目中，你不一定非得识别出图片中的物体是车辆，但你需要计算出其他车辆的位置，以确保自己能够避开它们。
  所以在目标检测项目中，首先需要计算出图中有哪些物体，比如汽车，还有图片中的其他东西，再将它们模拟成一个个盒子，或用一些其他的技术识别出它们在图片中的位置。

  

• 图片风格迁移

  比如说你有一张图片，但你想将这张图片转换为另外一种风格。所以图片风格迁移，就是你有一张满意的图片和一张风格图片，实际上右边这幅画是毕加索的画作，而你可以利用神经网络将它们融合到一起，描绘出一张新的图片。它的整体轮廓来自于左边，却是右边的风格，最后生成下面这张图片。这种神奇的算法创造出了新的艺术风格，所以在这门课程中，你也能通过学习做到这样的事情。

  

为什么需要卷积

但在应用计算机视觉时要面临一个挑战，就是数据的输入可能会非常大。

举个例子，在过去的课程中，你们一般操作的都是64×64的小图片，因为每张图片都有3个颜色通道，实际上它的数据量是64×64×3=12288。
这其实还好，因为64×64真的是很小的一张图片。

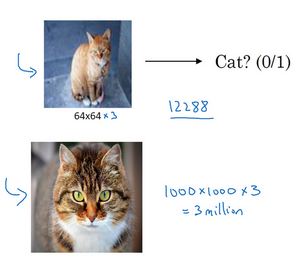
如果你要操作更大的图片，比如一张1000×1000的图片

• 输入量：像素足有1兆，因为有3个RGB通道，所以数据量将会是1000×1000×3=300万。即特征向量$x$的维度高达300万。
• 第一隐藏层：所以在第一隐藏层中，你也许会有1000个隐藏单元，而所有的权值组成了矩阵 $W^{[1]}$。
• 第一隐藏层的矩阵：如果你使用了标准的全连接网络，就像我们在第一门和第二门的课程里说的，这个矩阵的大小将会是1000×300万。
  因为现在$x$的维度为$3m$（$3m$通常用来表示300万）。这意味着矩阵$W^{[1]}$会有30亿个参数，这是个非常巨大的数字。

参数庞大的后果

• 难以获得足够的数据来防止神经网络发生过拟合和竞争需求。
• 而且要处理包含30亿参数的神经网络，巨大的内存需求让人不太能接受。

解决方法

• 但对于计算机视觉应用来说，你肯定不想它只处理小图片，你希望它同时也要能处理大图。
  为此，你需要进行卷积计算，我将用边缘检测的例子来向你说明卷积的含义。

边缘检测的例子（Edge detection）

卷积运算是卷积神经网络最基本的组成部分，使用边缘检测作为入门样例，你会看到卷积是如何进行运算的

边缘检测的示例

计算机视觉神经网络

• 前几层检测边缘
• 后面的层有可能检测到物体的部分区域
• 更靠后的一些层可能检测到完整的物体（这个例子中就是人脸）

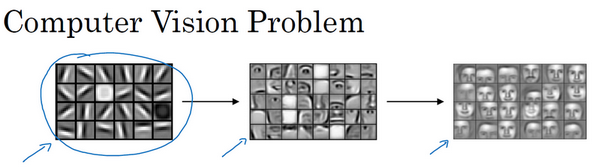
那么，图片如何进行边缘检测？

让我们举个例子，给了这样一张图片，让电脑去搞清楚这张照片里有什么物体

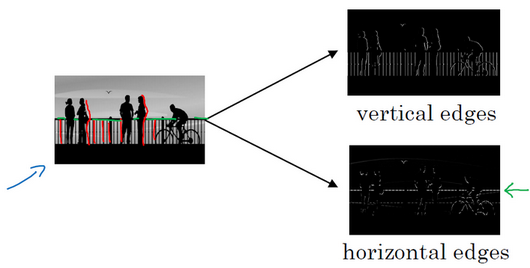
垂直和水平边缘检测：

你可能做的第一件事是检测图片中的垂直边缘

比如说，在这张图片中的栏杆就对应垂直线，与此同时，这些行人的轮廓线某种程度上也是垂线，这些线是垂直边缘检测器的输出。
同样，你可能也想检测水平边缘，比如说这些栏杆就是很明显的水平线，它们也能被检测到

所以如何在图像中检测这些边缘？

看一个例子，下图的左侧是一个6×6的灰度图像。
因为是灰度图像，没有RGB三通道，所以它是6×6×1的矩阵（而不是6×6×3）

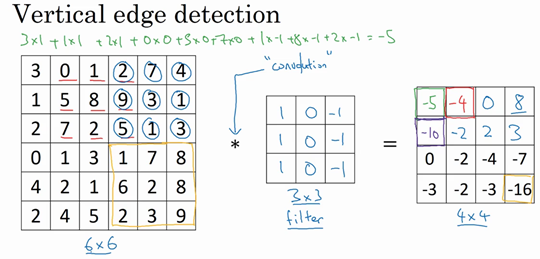
过滤器 / 核 / 卷积核（filter / kernel / convolution kernel）

为了检测图像中的垂直边缘，你可以构造一个3×3矩阵，像这样：

$$\begin{bmatrix}1 & 0 & -1\\ 1 & 0 & -1\\ 1 & 0 & -1\end{bmatrix}$$

在卷积神经网络的术语中，它被称为过滤器。在论文它有时候会被称为核或卷积核

卷积运算（convolution operation）

对这个6×6的图像进行卷积运算，卷积运算用“$*$”来表示，用3×3的过滤器对其进行卷积。

关于符号表示，有一些问题

在数学中“$*$”就是卷积的标准标志，
但是在Python中，这个标识常常被用来表示乘法或者元素乘法。

所以这个“$*$”有多层含义，它是一个重载符号，在这个视频中，当“$*$”表示卷积的时候我会特别说明。

卷积运算的计算：

这个卷积运算的输出将会是一个4×4的矩阵，你可以将它看成一个4×4的图像。

输出的第一个元素（4x4矩阵最左上角那个），使用3×3的过滤器，将其覆盖在输入图像

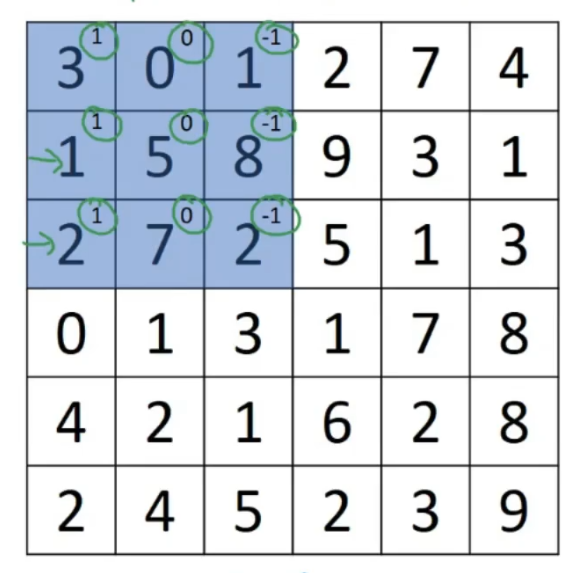
然后进行元素乘法（element-wise products）运算

即

$$~ \begin{align} Output[1][1] =& \sum\begin{bmatrix} 3 \times 1 & 0 \times 0 & 1 \times \left(1 \right) \\ 1 \times 1 & 5 \times 0 & 8 \times \left( - 1 \right) \\ 2 \times1 & 7 \times 0 & 2 \times \left( - 1 \right) \end{bmatrix} = \sum\begin{bmatrix} 3 & 0 & - 1 \\ 1 & 0 & - 8 \\ 2 & 0 & - 2 \\ \end{bmatrix}\\ =&~ 3+1+2+0+0 +0+(-1)+(-8) +(-2)\\ =&~ -5 \end{align}$$

同理，计算第二个元素，你要把蓝色的方块，向右移动一步
继续做同样的元素乘法，然后加起来，所以是 $0×1+5×1+7×1+1×0+8×0+2×0+2×(-1)+ 9×(-1)+5×(-1)=-4 $。

蓝色方块有16种位置，对应输出矩阵的16个元素的值

其中，输入左边矩阵为一张图片，中间矩阵为过滤器，输出的右边矩阵可以理解为另一张图片。这个就是垂直边缘检测器

原理（为什么可以边缘检测？）

为什么这个可以做垂直边缘检测呢？

为了讲清楚，我会用一个简单的例子。
这是一个简单的6×6图像，左边的一半是10，右边一般是0。
如果你把它当成一个图片，左边那部分比较亮，右边像素值比较暗。

（我使用灰色来表示0，尽管它也可以被画成黑的。用黑色表示-1）

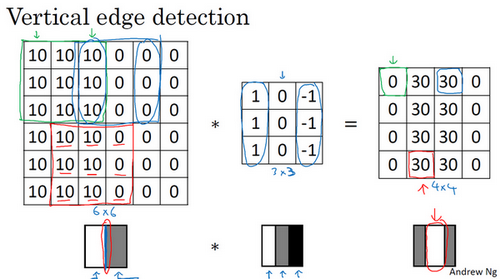
当你用一个3×3过滤器进行卷积运算的时候，卷积运算后，你得到的是右边的矩阵。

如果把最右边的矩阵当成图像，它是这个样子。在中间有段亮一点的区域，亮的区域对应检查到这个6×6图像中间的垂直边缘。

• 绿色框对应的值：没有边缘
• 红色/蓝色框对应的值：表示有边缘

这里的维数似乎有点不正确，检测到的边缘太粗了。那是因为在这个例子中，图片太小了。
如果你用一个1000×1000的图像，而不是6×6的图片，你会发现其会很好地检测出图像中的垂直边缘。
在这个例子中，在输出图像中间的亮处，表示在图像中间有一个特别明显的垂直边缘

因为我们使用3×3的矩阵（过滤器），所以垂直边缘是一个3×3的区域，左边是明亮的像素，中间的并不需要考虑，右边是深色像素。
在这个6×6图像的中间部分，明亮的像素在左边，深色的像素在右边，就被视为一个垂直边缘，卷积运算提供了一个方便的方法来发现图像中的垂直边缘。

更复杂的例子

这里还有个更复杂的例子
如果你将它绘成图片，右上角和左下角是比较暗的地方，而左上方和右下方都会相对较亮。

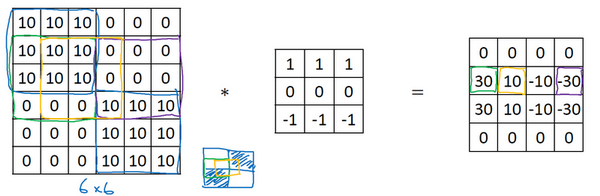
如果你用这幅图与水平边缘过滤器卷积，就会得到右边这个矩阵。

• 蓝色方框：0
• 绿色/紫色方框：30/-30
• 黄色方框：10

过滤器 补充

更多边缘检测内容

正边和负边

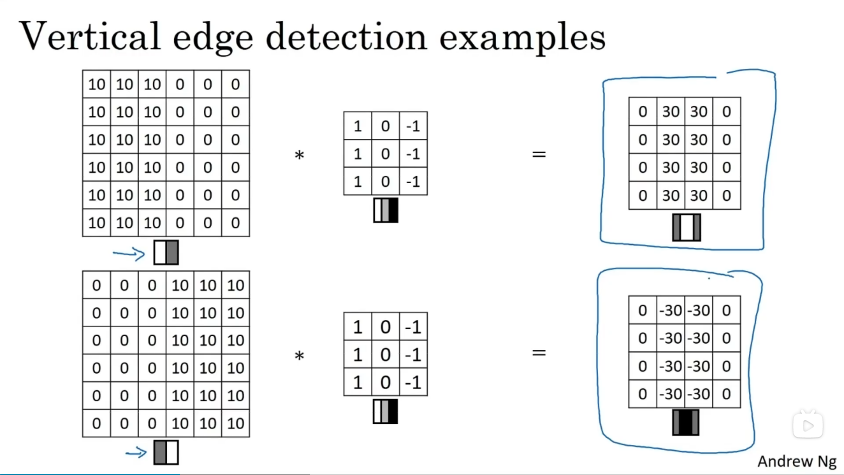
上图中，下面的输入矩阵和上面的输入矩阵相比，它的颜色被翻转了。或者叫正边和负边

如果你用它与相同的过滤器进行卷积，最后得到的图中间会是-30，而不是30。

如果你不在乎这两者的区别，你可以取出矩阵的绝对值。

但这个特定的过滤器确实可以为我们区分这两种明暗变化的区别。

垂直检测和水平检测

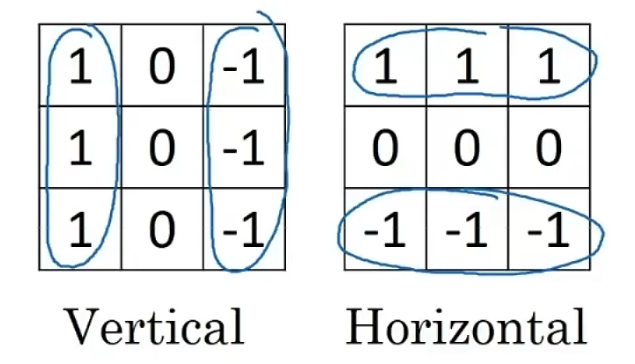
左边这个3×3的过滤器，它可以检测出垂直的边缘。
右边这个3x3的过滤器，它可以检测出水平的边缘。

其他过滤器

在历史上，在计算机视觉的文献中，曾公平地争论过怎样的数字组合才是最好的

普通的过滤器

普通的垂直或水平过滤器

$$\begin{align} &~~垂直& &~~水平\\ &\begin{bmatrix}1 & 0 & - 1 \\ 1 & 0 & - 1 \\ 1 & 0 & - 1 \\\end{bmatrix}& &\begin{bmatrix}1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & - 1 \\\end{bmatrix} \end{align}$$

Sobel的过滤器

Sobel过滤器

$$\begin{bmatrix}1 & 0 & - 1 \\ 2 & 0 & - 2 \\ 1 & 0 & - 1 \\\end{bmatrix}$$

优点：在于增加了中间一行元素的权重，这使得结果的鲁棒性会更高一些

Scharr过滤器

Scharr过滤器

$$\begin{bmatrix} 3& 0 & - 3 \\ 10 & 0 & - 10 \\ 3 & 0 & - 3 \\\end{bmatrix}$$

这实际上也是一种垂直边缘检测，如果你将其翻转90度，你就能得到对应水平边缘检测

非手写的带参数的过滤器

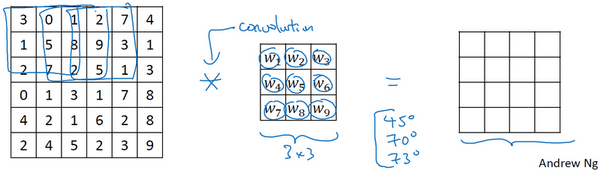
随着深度学习的发展，我们学习的其中一件事就是当你真正想去检测出复杂图像的边缘。

你不一定要去使用那些研究者们所选择的这九个数字。
你可以把这矩阵中的9个数字当成9个参数，并且在之后你可以学习使用反向传播算法，去算出这9个参数。

性能：

这种过滤器对于数据的捕捉能力甚至可以胜过任何之前这些手写的过滤器。
相比这种单纯的垂直边缘和水平边缘，它可以检测出45°或70°或73°，甚至是任何角度的边缘。

所以将矩阵的所有数字都设置为参数，通过数据反馈，让神经网络自动去学习它们。
我们会发现神经网络可以学习一些低级的特征，例如这些边缘的特征。

原理：

不过构成这些计算的基础依然是卷积运算。
任何它所检测到的特征，不管是垂直的边缘，水平的边缘，还有其他奇怪角度的边缘，甚至是其它的连名字都没有的过滤器。

所以这种将这9个数字当成参数的思想，已经成为计算机视觉中最为有效的思想之一。

如何使用反向传播去让神经网络学习这9个数字？这个后面再讲

卷积运算 补充

卷积运算的编程实现

如果你要使用编程语言实现卷积运算，不同的编程语言有不同的函数，而不是用“$*$”来表示卷积。

所以在python编程练习中，你会使用一个叫conv_forward的函数。
如果在tensorflow框架下，这个函数叫tf.conv2d。
如果在Keras框架下，用Conv2D实现卷积运算。

所有的编程框架都有一些函数来实现卷积运算。

互相关与卷积（Cross-correlation & Convolution）

数学教材和深度学习文献中的，卷积的定义不同

数学定义

卷积定义：（教科书中 / 信号处理书籍中的定义）

镜像过滤器并做元素乘积求和 / 镜像过滤器并进行互相关操作

就是在把这个6×6的矩阵和3×3的过滤器卷积之前，首先你将3×3的过滤器沿水平和垂直轴翻转。

$$即：将 \begin{bmatrix}3 & 4 & 5 \\ 1 & 0 & 2 \\ - 1 & 9 & 7 \\ \end{bmatrix} 变为 \begin{bmatrix} 7& 2 & 5 \\ 9 & 0 & 4 \\ - 1 & 1 & 3 \\\end{bmatrix}\\ （整理者注：此处应该是先顺时针旋转90度再水平翻转，\\ 或其沿着反对角线翻转）$$

好处：

卷积的定义包含翻转，使得卷积运算符拥有结合律这个性质

$$(A*B)*C=A*(B*C)\\ \text{其中，符号*表示卷积}$$

深度学习定义

卷积定义：（深度学习文献中的定义）

不镜像过滤器，直接做元素乘积求和
在数学的定义中，这个操作其实应该被称为：互相关 / 交叉相关（cross-correlation）而不是卷积（convolution）

根据惯例，我们大多数人都叫它卷积，尽管数学家们更喜欢称之为互相关

不进行镜像操作的原因：

镜像操作这对于一些信号处理应用来说很好，可以让卷积使用结合律。
但对于深度神经网络来说它真的不重要，因此省略了这个双重镜像操作，就简化了代码，神经网络也能正常工作

卷积参数

卷积填充（Padding）

为了构建深度神经网络，你需要学会使用的一个基本的卷积操作就是padding

之前的例子中：

$$\begin{align} 输入图像的shape=& 6×6\\ 做卷积的过滤器shape=& 3×3\\ 则输出的shape=& 4×4 \end{align}$$

通用的数学公式为：

$$\begin{align} 输入图像的shape=& n×n\\ 做卷积的过滤器shape=& f×f\\ 则输出的shape=& (n-f+1)×(n-f+1) \end{align}$$

但这样的话会有两个缺点：

• ① 每次做卷积操作，你的图像就会缩小

  比如从6×6缩小到4×4，你可能做了几次之后，你的图像就会变得很小了，可能会缩小到只有1×1的大小

• ② 在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息

  如果你注意角落边缘的像素，比如最右上角的像素点只被一个输出所触碰或者使用
  但如果是在最中间的像素点，就会有许多3×3的区域与之重叠（9个）。

解决方案：（Padding）

为了解决这些问题，你可以在卷积操作之前填充这幅图像。
在这个案例中，你可以沿着图像边缘再填充一层像素。

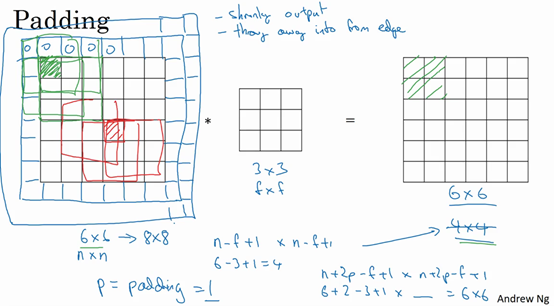
对比：

$$\begin{align} \color{red}原来的情况& & \color{red}进行边缘填充~(p=1)&\\ 输入图像的shape=& 6×6 & 输入图像的shape=& {\color{red}8×8} \\ 做卷积的过滤器shape=& 3×3 & 做卷积的过滤器shape=& 3×3 \\ 则输出的shape=& 4×4 & 则输出的shape=& {\color{red}6×6} \end{align}$$

• 填充数量：$p$是填充的数量，在这个案例中，$p=1$
• 填充内容：习惯上，你可以用0去填充

至于选择填充多少像素？通常有两个选择

• Valid卷积
• Same卷积

Valid卷积

Valid卷积：不填充

$$\begin{align} \color{red}公式& & \color{red}例如&\\ 输入图像的shape=& n×n & 输入图像的shape=& 6×6 \\ 做卷积的过滤器shape=& f×f & 做卷积的过滤器shape=& 3×3 \\ 则输出的shape=& (n-f+1)×(n-f+1) & 则输出的shape=& 4×4\\ & 或看成是~\color{red}p=0 \end{align}$$

Same卷积

Same卷积：填充后，你的输出大小和输入大小是一样的。

$$\begin{align} \color{red}公式& & \color{red}例如&\\ 输入图像的shape=& n×n & 输入图像的shape=& 6×6 \\ 填充后输入图像的shape=& (n+2p)×(n+2p) & 填充后输入图像的shape=& 6×6 \\ 做卷积的过滤器shape=& f×f & 做卷积的过滤器shape=& 3×3 \\ 则输出的shape=& (n+2p-f+1)×(n+2p-f+1) & 则输出的shape=& 6×6\\ =& n×n\\ &解得~\color{red}p=(f-1)/2 \end{align}$$

当$f$是一个奇数的时

只要选择相应的填充尺寸，能确保得到和输入相同尺寸的输出

例如：

• 当过滤器是3×3，$f=3$，所需要的填充是$(3-1)/2=1$像素
• 当过滤器是5×5，$f=5$，所需要的填充是$(5-1)/2=2$像素

习惯上，计算机视觉中，$f$通常是奇数，甚至可能都是这样。

当$f$是一个偶数的时（一般不会是偶数）

但实际上你很少看到一个偶数的过滤器在计算机视觉里使用，我认为有两个原因

• 原因一

  如果$f$是一个偶数，那么你只能使用一些不对称填充。
  只有$f$是奇数的情况下，Same卷积才会有自然地 以同样的数量地 填充四周，而不是左边填充多一点，右边填充少一点

• 原因二

  当你有一个奇数维过滤器，比如3×3或者5×5的，它就有一个中心点。有中心点会更方便，便于指出过滤器的位置。

• 其他原因

  也许这些都不是为什么$f$通常是奇数的充分原因
  但如果你看了卷积的文献，你经常会看到3×3的过滤器，你也可能会看到一些5×5，7×7的过滤器，甚至1×1的过滤器。

  我想如果你使用偶数$f$也可能会得到不错的表现，如果遵循计算机视觉的惯例和习惯上，我只使用且推荐你只使用奇数值的$f$。

卷积步长（Strided convolutions）

卷积步长 / 卷积步幅

举例

如果你想用3×3的过滤器卷积这个7×7的图像，和之前不同的是，我们把步幅设置成了2。步幅用$s$表示，这里$s=2$

你还和之前一样取左上方的3×3区域的元素的乘积，再加起来，最后结果为91。
只是之前我们移动蓝框的步长是1，现在移动的步长是2，我们让过滤器跳过2个步长。
然后你还是将每个元素相乘并求和，你将会得到的结果是100。

后面的操作同理

这个例子中，我们用3×3的矩阵卷积一个7×7的矩阵，得到一个3×3的输出

通用公式

$$\begin{align} \color{red}公式& & \color{red}例如& \\ 填充\text{ padding}~=& p=(f-1)/2 & 填充\text{ padding}~=& p=0 \\ 步长\text{ strided}~=& s & 步长\text{ strided}~=& s=2 \\ 输入图像的shape=& n×n & 输入图像的shape=& 7×7 \\ 填充后输入图像的shape=& (n+2p)×(n+2p) & 填充后输入图像的shape=& 7×7 \\ 做卷积的过滤器shape=& f×f & 做卷积的过滤器shape=& 3×3 \\ 则输出的shape=& (\frac{n+2p-f}{s}+1) \times (\frac{n+2p-f}{s}+1) & 则输出的shape=& 3×3\\ \end{align}$$

如果商不是一个整数怎么办？

这里指$\frac{n + 2p - f}{s}$的商不是一个整数

在这种情况下，我们向下取整。$⌊ ⌋$这是向下取整的符号，这也叫做对$z$进行地板除 (floor)，这意味着$z$向下取整到最近的整数。

形象一点的解释是：
你只在蓝框完全包括在图像或填充完的图像内部时，才对它进行运算。
如果有任意一个蓝框通过大步幅移动到了外面，那你就不要进行操作。

三维卷积（Convolutions over volumes）

RGB卷积

你已经知道如何对二维图像做卷积了，现在看看如何执行卷积不仅仅在二维图像上，而是三维立体上。

我们从一个例子开始，假如说你不仅想检测灰度图像的特征，也想检测RGB彩色图像的特征。
彩色图像如果是6×6×3，这里的3指的是三个颜色通道，你可以把它想象成三个6×6图像的堆叠。
为了检测图像的边缘或者其他的特征，不是把它跟原来的3×3的过滤器做卷积，而是跟一个三维的过滤器，它的维度是3×3×3

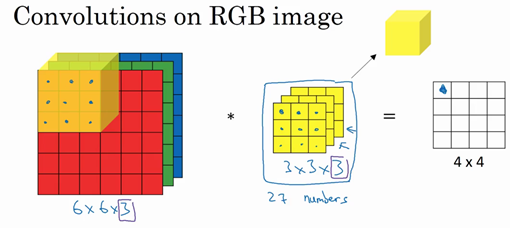
计算过程和之前大同小异：

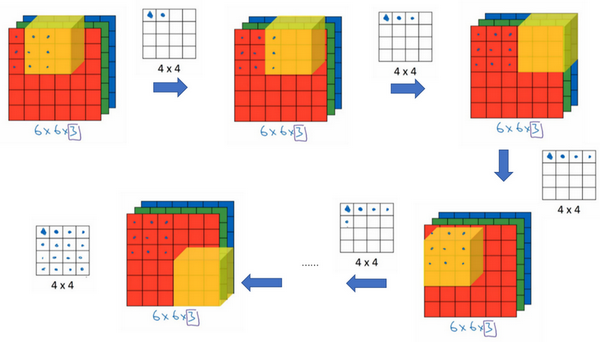
那么，这个能干什么呢？举个例子

如果你想检测图像红色通道的边缘：（或者只关注绿色或者蓝色通道也行）

$$红色过滤器：\begin{bmatrix}1 & 0 & - 1 \\ 1 & 0 & - 1 \\ 1 & 0 & - 1 \\\end{bmatrix}\\ 绿色和蓝色过滤器：\begin{bmatrix} 0& 0 & 0 \\ 0 &0 & 0 \\ 0 & 0 & 0 \\\end{bmatrix}\\ 把这三个堆叠在一起形成一个3×3×3的过滤器，那么这就是一个{\color{red}只对红色通道有用}的检测垂直边界的过滤器$$

如果你不关心垂直边界在哪个颜色通道里，那么你可以用一个这样的过滤器：

$$三个通道都是这样\\ \begin{bmatrix}1 & 0 & - 1 \\ 1 & 0 & - 1 \\ 1 & 0 & - 1 \\ \end{bmatrix}， \begin{bmatrix}1 & 0 & - 1 \\ 1 & 0 & - 1 \\ 1 & 0 & - 1 \\ \end{bmatrix}， \begin{bmatrix}1 & 0 & - 1 \\ 1 & 0 & - 1 \\ 1 & 0 & - 1 \\\end{bmatrix}$$

同时使用多个过滤器

如果我们不仅仅想要检测垂直边缘怎么办？如果我们同时检测垂直边缘和水平边缘，还有45°倾斜的边缘，还有70°倾斜的边缘怎么做？
换句话说，如果你想同时用多个过滤器怎么办？

我们让这个6×6×3的图像和这个3×3×3的过滤器卷积，得到4×4的输出
第一个过滤器（黄色表示）可能是一个垂直边界检测器
第二个过滤器（橘色表示）可以是一个水平边缘检测器

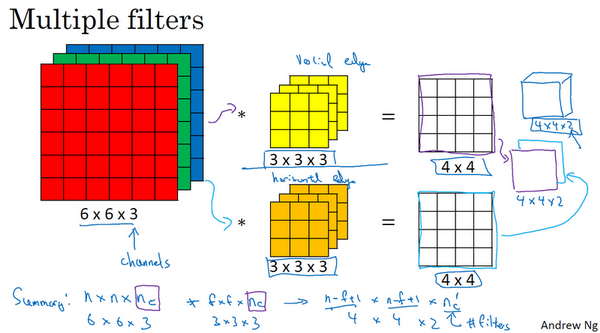
所以和第一个过滤器卷积，可以得到第一个4×4的输出，然后卷积第二个过滤器，得到一个不同的4×4的输出。
我们做完卷积，然后把这两个4×4的输出，取第一个把它放到前面，然后取第二个过滤器放到后面。
所以把这两个输出堆叠在一起，这样你就都得到了一个4×4×2的输出立方体。

总结一下通用公式

$$\begin{align} \color{red}公式& & \color{red}例如& \\ 填充\text{ padding}~=& p=(f-1)/2 & 填充\text{ padding}~=& p=0 \\ 步长\text{ steps}~=& s & 步长\text{ steps}~=& s=1 \\ 输入图像的shape=& n×n×\color{red}n_c & 输入图像的shape=& 6×6×3 \\ 填充后输入图像的shape=& (n+2p)×(n+2p)×\color{red}n_c & 填充后输入图像的shape=& 6×6×3 \\ 做卷积的过滤器shape=& f×f×\color{red}n_c & 做卷积的过滤器shape=& 3×3×3 \\ 则输出的shape=& (\frac{n+2p-f}{s}+1) × (\frac{n+2p-f}{s}+1) × \color{red}n_c& 则输出的shape=& 4×4×4\\ \end{align}$$

（其中，$n_c$是通道数，$n_{c^{'}}$是下一层的通道数
通道数在文献里大家也把它叫做3维立方体的深度）