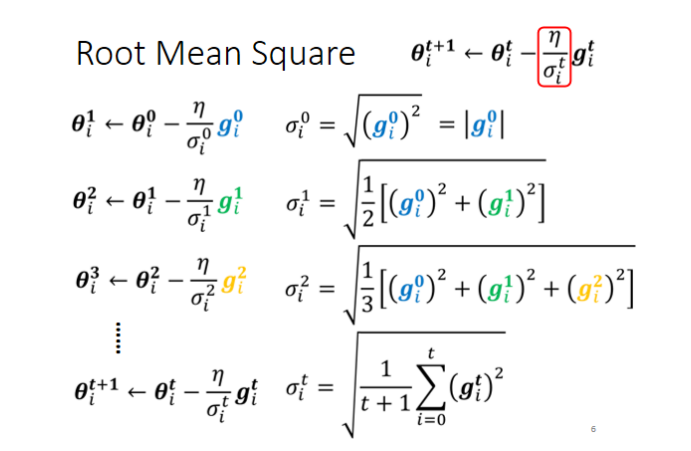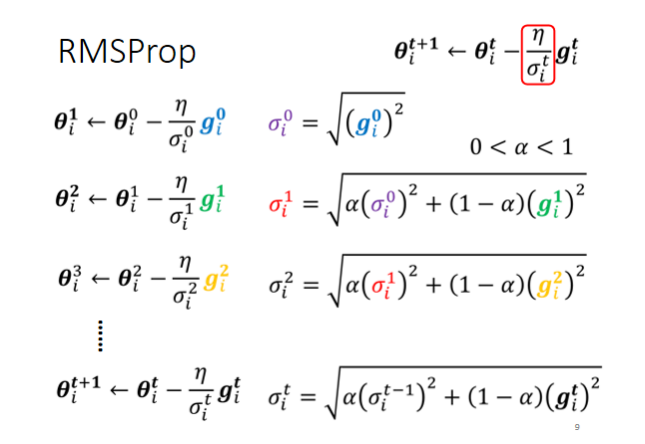李宏毅机器学习深度学习

目录

自动调整学习率

对应视频：P21
对应pdf：06_Adaptive Learning Rate.pdf

Training stuck ≠ Small Gradient（训练停滞 ≠ 小梯度）

Training stuck ≠ critical point（临界点），不等于gradient$\approx$0

学习率衰减

吴恩达笔记

各种学习率衰减公式：

• $a= \frac{1}{1 + \text{decay-rate} * \text{epoch-num}}a_{0}= \frac{1}{1 + 衰减率 * 代数}\text{初始学习率}$，当前公式，包括超参数$a_{0}$和衰减率

• $a ={0.95}^{\text{epoch-num}} a_{0}$，指数衰减，学习率呈指数下降

• $a =\frac{k}{\sqrt{\text{epoch-num}}}a_{0}$

• $a =\frac{k}{\sqrt{t}}a_{0}$（$t$为mini-batch的数字）。

• 有时人们也会用一个离散下降（discrete stair cease）的学习率。

  也就是某个步骤有某个学习率，一会之后，学习率减少了一半，一会儿减少一半，一会儿又一半

• 人们有时候还会做一件事，手动衰减。

李宏毅笔记

均方根版

和吴恩达版所使用的自动调整学习率的方法不同

$$\begin{aligned} 原来的梯度下降\\ \theta_i^{t+1}:=& \theta_i^t-\mu g_i^t\\ g_i^t=& \frac{\partial L}{\partial \theta_i}|_{\theta=\theta^t}\\~\\ 学习率衰减版梯度下降\\ \theta_i^{t+1}:=& \theta_i^t-\frac\mu{\sigma_i^t} g_i^t \end{aligned}$$

这里说白了就是$a:=a/均方根$，均方也叫平方平均数

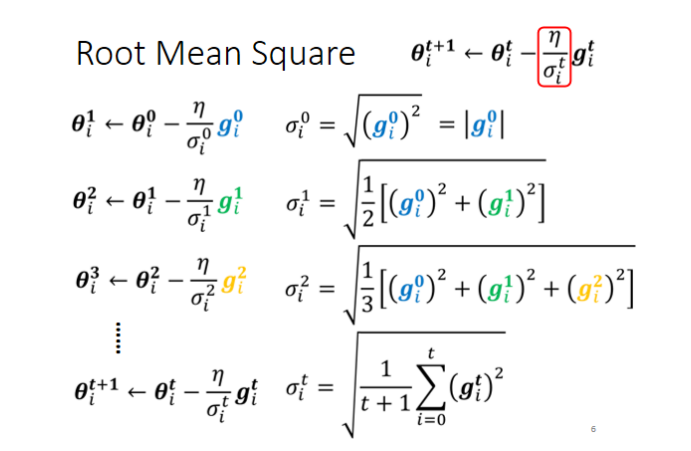
Learning Rate Scheduling（时间衰减）

但是注意：如果只用均方根衰减学习率可能会有以下问题：

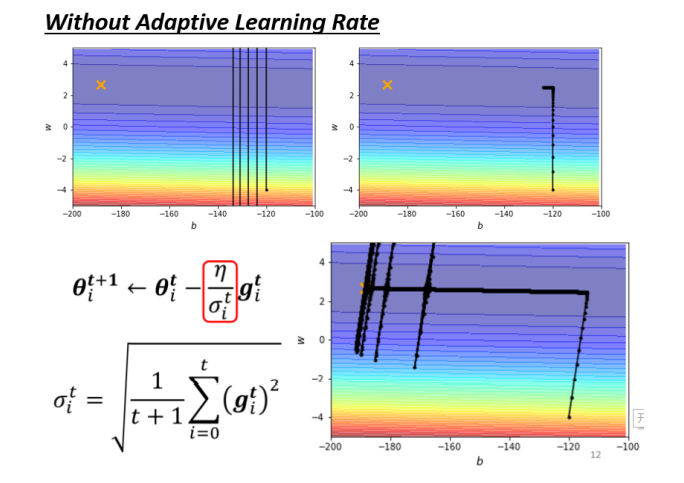
原因分析：

• 所以这个纵轴的方向,在这个初始的这个地方,感觉gradient很大
• 可是这边走了很长一段路以后,这个纵轴的方向,gradient算出来都很小,所以纵轴这个方向,这个y轴 的方向就累积了很小的σ
• 因為我们在这个y轴的方向,看到很多很小的gradient,所以我们就累积了很小的σ,累积到一个地步以 后,这个step就变很大,然后就爆走就喷出去了
• 喷出去以后没关係,有办法修正回来,因為喷出去以后,就走到了这个gradient比较大的地方,走到 gradient比较大的地方以后,这个σ又慢慢的变大,σ慢慢变大以后,这个参数update的距离,Update的 步伐大小就慢慢的变小

解决方法：Learning Rate Scheduling（学习率的时间调度）

$$\theta_i^{t+1}:= \theta_i^t-\frac{\mu^{\color{red}t}}{\sigma_i^t} g_i^t$$

Warm Up（热身）

另一个解决方法是 Warm Up，让learning rate先变大后变小

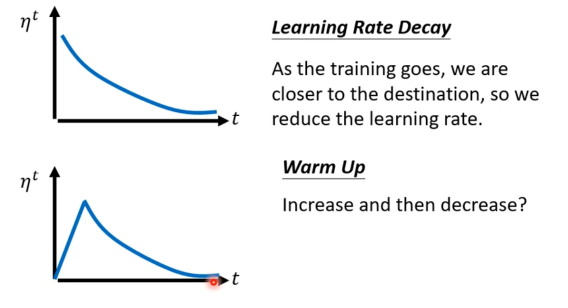
这个有点 “黑科技”，为什么有的模型学习率要先变大后变小才能获得更好的效果？
没有一个完美的解释，依然是有点玄学
其中一个解释是，不要一开始走太远，要先在初始化的点做一些 “探索”，冷启动

RMSProp

吴恩达笔记

$$~ \begin{align} S_{dW}=& \beta_2 S_{dW} + (1 -\beta_2) {dW}^{\color{red}2}\\ S_{db}=& \beta_2 S_{db} ~~+ (1 -\beta_2) {db}^{\color{red}2}\\~\\ W:=& W -a\cdot \frac{dw}{\sqrt{S_{dW}}}\\ b:=& b~~-a\cdot \frac{db}{\sqrt{S_{db}}} \end{align}\\~\\ {\color{red}注意这个平方的操作}是针对这一整个符号的操作，这样做能够保留微分平方的加权平均数\\ 即dW^2=(dW)^2\neq d(W^2)$$

李宏毅笔记

（和吴恩达笔记中不同的是，这里理解为分别调整各种方向的学习率，而吴恩达课程中理解为调整梯度的方向）
而且公式上，两者也略有不同

之前调整学习率是一起调的
但对于不同参数不同方向，我们也期待说learning rate是可以动态的调整的，于是就有了RMS Prop

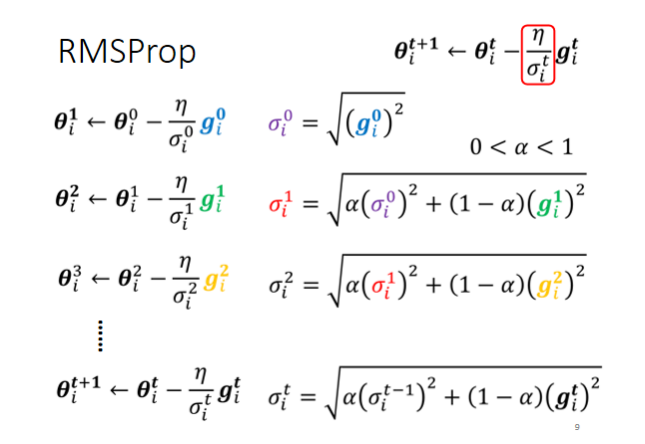
Adam

RMSProp + Momentum

有个进阶版叫 RAdam

总结

$$\begin{aligned} 原来的梯度下降\\ \theta_i^{t+1}:=& \theta_i^t-\mu g_i^t\\~\\ 学习率自调整版\\ \theta_i^{t+1}:=& \theta_i^t-\frac\mu{\sigma_i^t} g_i^t\\~\\ 加上学习率衰减\\ \theta_i^{t+1}:=& \theta_i^t-\frac{\mu^{\color{red}t}}{\sigma_i^t} g_i^t\\~\\ 加上Adam\\ \theta_i^{t+1}:=& \theta_i^t-\frac{\mu^{\color{red}t}}{\sigma_i^t} \color{red}m_j^t \end{aligned}$$

001

002
003

004

005

1

2

3

4

651463

4165

6351313

213

51461