李宏毅机器学习深度学习

分类

（按道理这节的类别有点问题）

对应视频：P22
对应pdf：08_Classification.pdf（06到08跳过了07，07_Batch Normalization.pdf没有对应视频）

略

两个就用Sigmoid，但其实和Softmax是等价的

Softmax：

y'_i = \frac{\exp(y_i)}{\sum_j\exp(y_i)}

\begin{aligned} \text{Mean Square Error (MSE)}，& 平方误差 & e=&\sum_i (\hat y_i-y_i')^2\\ \text{Cross-entropy}，& 信息论里的交叉熵 & e=&-\sum_i \hat y_i\ln y_i' \end{aligned}

回归函数一般用前者，而分类问题一般用交叉熵

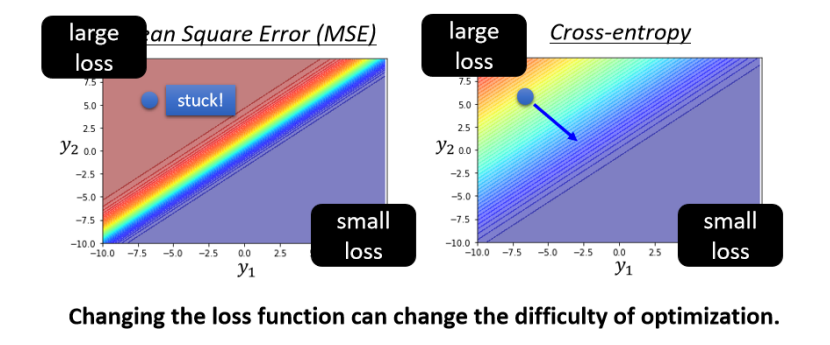
那假设我们开始的地方,都是左上角

如果选择Cross-Entropy
左上角这个地方,它是有斜率的,所以你有办法透过gradient,一路往右下的地方走,
如果选择Mean square error
你就卡住了，Mean square error在这种Loss很大的地方，它是非常平坦的，它的gradient是非常小趋近於0的，如果你初始的时候在这个地方，离你的目标非常远，那它 gradient又很小，你就会没有办法用gradient descent，顺利的走到右下角的地方去

（TODO：Understand，这一节不是太明白，还没有pdf可以参考。这章又tm很长，一个多小时，等有时间再重新看一次吧）
$h$ 的概念有点难理解

我们希望L({\color{cyan}h^{train}},{\color{red}D_{all}})和L({\color{red}h^{all}},{\color{red}D_{all}})尽可能小\\~\\ 如何让理想和现实接近？什么样的D_{train}可以让理想和现实接近？应该就是在问如何让训练集和测试集更接近\\ 后者必定小于前者，但我们希望他两尽可能相似\\~\\ 要满足：\\ L({\color{cyan}h^{train}},{\color{red}D_{all}}) - L({\color{red}h^{all}},{\color{red}D_{all}})\leq \delta\\ 只要满足:\\ \forall {\color{green}h}\in H,|L({\color{green}h},{\color{cyan}D_{train}})-L({\color{green}h},{\color{red}D_{all}})|\leq \delta/2\\ h是穷举所有可能的数据

还能推得：

~ \begin{aligned} L({\color{cyan}h^{train}},{\color{red}D_{all}}) & \leq L({\color{cyan}h^{train}},{\color{cyan}D_{train}}) +\delta\\ & \leq L({\color{red}h^{all}},{\color{cyan}D_{train}})\\ & \leq L({\color{red}h^{all}},{\color{red}D_{all}})+\delta/2+\delta/2 \end{aligned}\\ \varepsilon=\delta/2

证明：

略

例如：

\begin{aligned} &|H|=10000，N=100，~~\varepsilon=0.1 & P(D_{train}~is~bad)&\leq 2701\\ &|H|=10000，N=500，~~\varepsilon=0.1 & P(D_{train}~is~bad)&\leq 0.91\\ &|H|=10000，N=1000，\varepsilon=0.1 & P(D_{train}~is~bad)&\leq 0.00004\\~\\ |H| &：是\\ N &：每次随机采样的量\\ \varepsilon &：是 \end{aligned}

经验

我们要比较大的N，比较小的|H|，这样能更好地满足 $L({\color{cyan}h^{train}},{\color{red}D_{all}}) - L({\color{red}h^{all}},{\color{red}D_{all}})\leq \delta$

链接到当前文件 0

没有文件链接到当前文件