微积分

目录

导数

定理总结

基本求导法则与导数公式（要背）

导数公式

• 导数公式【1】常量 / 幂函数类

  • $(C)'=0$
  • $(x^\mu)'=\mu x^{\mu-1}$

• 导数公式【2】三角与反三角类

  • \begin{align} (\sin x)'&=\cos x& (\cos x)'&={\color{red}-}\sin x\\ (\tan x)'&=\sec^2 x& (\cot x)'&={\color{red}-}\csc^2 x\\ (\sec x)'&=\sec x\tan x& (\csc x)'&={\color{red}-}\csc x\cot x\\ (\arcsin x)'&=\frac1{\sqrt{1-x^2}}& (\arccos x)'&={\color{red}-}\frac1{\sqrt{1-x^2}}\\ (\arctan x)'&=\frac1{1+x^2}& (arccot~x)'&={\color{red}-}\frac1{1+x^2}'\\ (arcsec~x)'&=\frac{1}{|x|\sqrt{x^2-1}}&(arccsc~x)'&={\color{red}-}\frac{1}{|x|\sqrt{x^2-1}} \end{align}

• 导数公式【3】对数指数类

  • \begin{align} &（1）(a^x)'=a^x\ln a（a>0,a\neq1） &&（2）(e^x)'=e^x\\ &（3）(log_ax)'=\frac1{x\ln a}（a>0,a\neq1) &&（4）(\ln x)'=\frac1x \end{align}

求导法则（精简版）

• 求导法则【定理1简写】和差积商：\begin{align} &（1）(u\pm v)'=u'\pm v' &&（2）(Cu)'=Cu'（C是常数）\\ &（3）(uv)'=u'v+uv' &&（4）(\frac{u}{v})'=\frac{u'v-uv'}{v^2}（v\neq0） \end{align}
• 求导法则【定理2】反函数：$[f^{-1}(x)]'=\frac 1{f'(y)}~~或~~\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}$
• 求导法则【定理3】复合函数：$f'(x)=f'(u)\cdot g'(x)或\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$

三角函数补充（自增）

image-20201106153638294

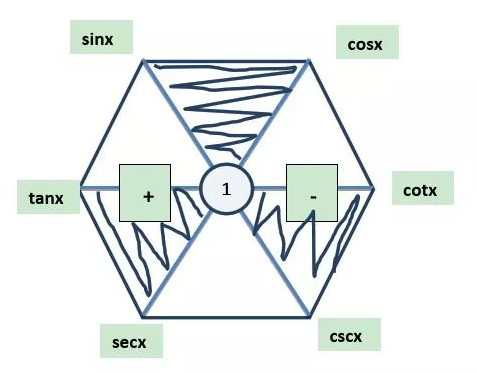
非显函数求导

• 隐函数求导方法

  • 把方程两边分别对x求导数
  • 注意：$y看作x的复合函数，通常f(y)'的结果为g(y,y')\\ y'=y'，x'=1，0'=0$

• 参数方程求导方法

  • $$\frac{dy}{dx}=\frac {~\frac{dy}{dt}~} {\frac{dx}{dt}}$$