吴恩达机器学习

目录

第二课导读

• 神经网络（Neural Networks）
  • 推理（预言）
  • 训练
• 建立机器学习系统的一些实用建议
• 决策树（Decision Tree）

神经网络（Neural Networks）

入门

入门

起源

模拟神经元和大脑（Neuron & Brain）

研究历史

• 起源：1950年尝试去模拟大脑
• 1980~1990年，再次流行
• 2005年，兴起
• 神经网络近期增长，也很大程度因为数据的数量多了很多，即大数据。这得以去训练大型神经网络

大脑如何运行？

• 一个神经元可以影响输出其他神经元，神经元包括树突轴突神经末梢等，……
• 简化数学模型：输入神经元影响输出神经元，神经元可以影响多个神经元，神经元也可以被多个神经元影响

神经网络为何如此高效

CPU GPU 能并行运算，擅长做非常大的矩阵运算，矩阵运算通常也是可并行计算的

在编程时应该尽量用矩阵运算去代替for循环，以提高运算效率

概念

激活函数（Activation Function）

定义一个激活函数，一般选择Sigomid作为激活函数

$$a=g(x)=\frac1{1+e^{-(wx+b)}}\\ 其中a是激活~activation~的意思，这个函数也叫激活函数$$

写程序时也经常将这个激活函数分两条语句：

$$\begin{cases} z=wx+b\\ a=g(z)=\frac1{1+e^{-z}} \end{cases}$$

即

z = np.dot(w,x) + b
f_x = 1/(1+mp.exp(-z))

神经元（Neuron）/ 单元（Units）

对于一个 Neuron (神经元) 来说，对他输入x便会根据激活函数输出a

这里的神经元在机器神经网络中也被简称为单元（Units）

层（Layer）

• 层

  • 层（Layer），说详细点也可以叫 神经网络层（Neural Network Layer）

  • 一个神经网络有一或多个层，每一层可以有一或多个 Neuron

  • 同一层的 Neuron 有相同的特性

    例如：同一层中的每一个 Neuron 他们的激活函数模型一样 (比如都是Sigmoid)，但是函数中的参数可能不一样（例如w和b不同）

• 层包括

  • 这些层包含输入层（Input Layout）、 输出层（Output Layouts）、中间层 / 隐藏层（Middle Layer / Hidden Layer）
    • 输入层补充：不包含 Neuron，就是原始数据
    • 输出层补充：一般只有一个 Neuron，得到最终结果
    • 中间层补充：也叫做隐藏层的原因是，在训练集中，只能看到输入和输出结果，中间的过程不能看 (也看不懂)
  • 层的计数是从0开始的。例如输入层和输出层直接有三个中间层，他们分别是 “Layer0~Layer4”

• 向量化

  • 不同层之间的 Neuron，上一层的每个 Neuron 输出给下一层的所有 Neuron，下一层的每个 Neuron 接收上一层所有Neuron，即 “全射”
  • 一般将一个层中的所有 Neuron 包成一个向量，通过矩阵叉乘的方式就可以将上一个层全射到下一个层中

神经网络（Neural Networks）

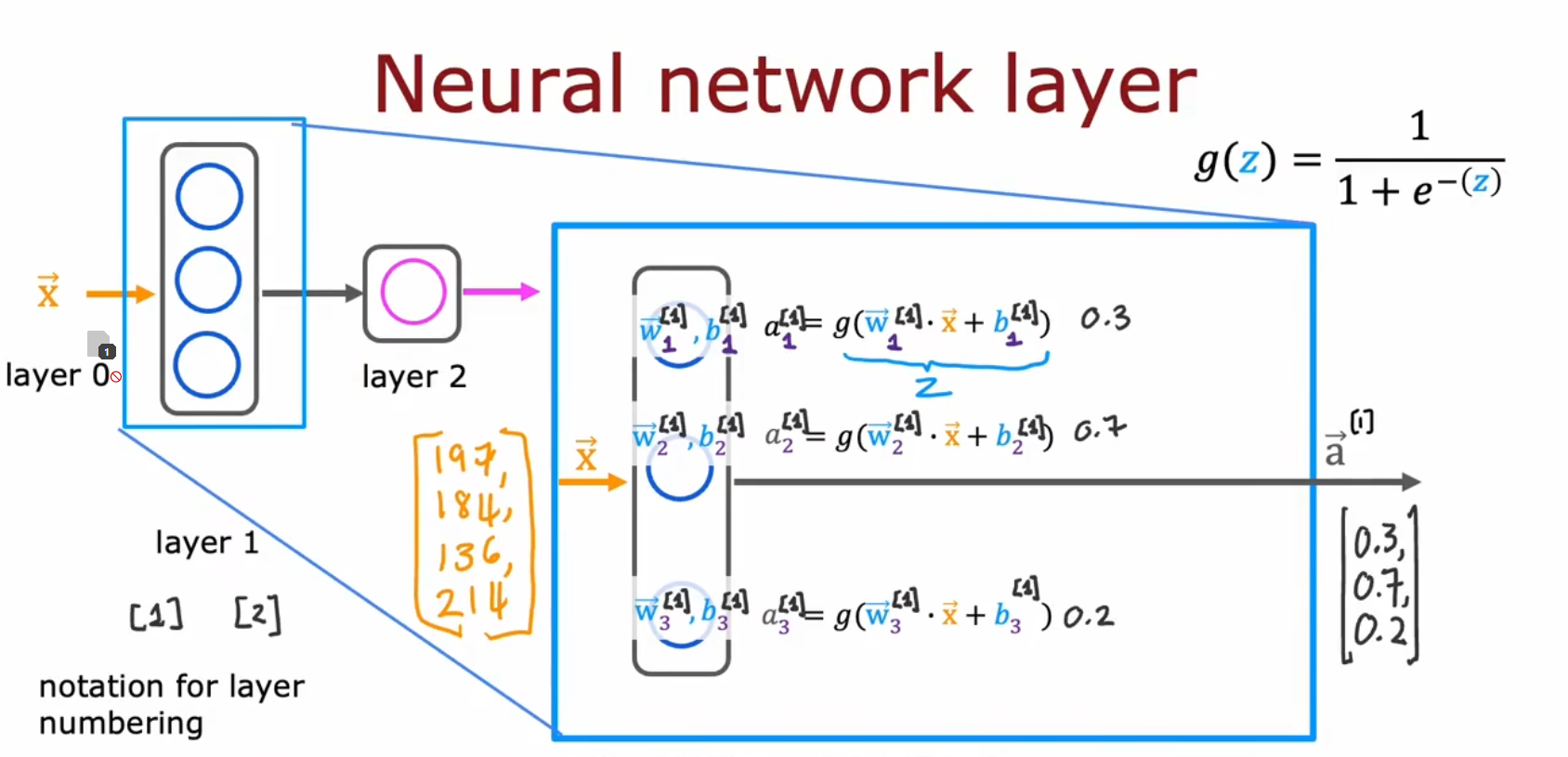
单中间层的结构

每一个 Neuron 都有一个Sigmoid的激活函数

符号表示

• 右上角加$[~]$的上标表示处于第几个网络层
• 右上角加$()$的上标表示用的是第几个样本（当然，在向量化的公式里你看不到这个表示的，而且一般也是用下标表示的）
• 右下角数字$j$的下标表示是该网络层的第$j$个单元。是输入层的第$j$个特制，其中$x^{(1)}\not=x_1$
• $w_j^{[l]}、b_j^{[l]}$表示处于第$l$个神经网络层的第$j$个神经元所使用Sigmoid函数的参数
• $\vec x$表示输入层的矢量表示，等价于$\vec a^{[l]}$
• $\vec a^{[l]}$表示序列$l$ (注意从0开始计数) 的神经网络层的输出的矢量表示

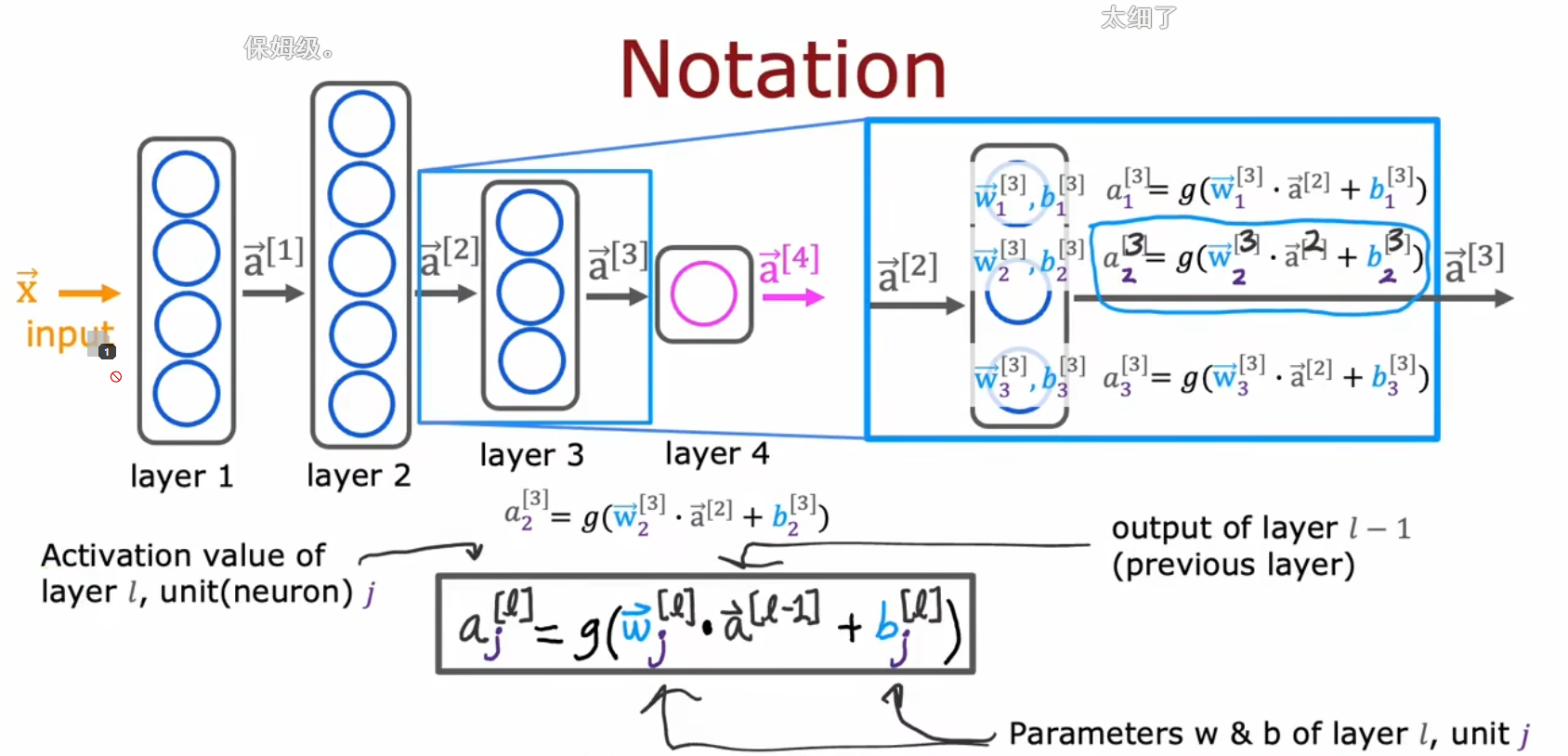
多中间层的结构

$$a_j^{[l]}=g(\vec w_j^{[l]}\cdot \vec a^{[l-1]}+b_j^{[l]})$$

符号表示

• 右上角加$[~]$的上标表示处于第几个网络层
• 右上角加$()$的上标表示用的是第几个样本（当然，在向量化的公式里你看不到这个表示的，而且一般也是用下标表示的）
• 右下角数字$j$的下标表示是该网络层的第$j$个单元。是输入层的第$j$个特制，其中$x^{(1)}\not=x_1$
• $w_j^{[l]}、b_j^{[l]}$表示处于第$l$个神经网络层的第$j$个神经元所使用Sigmoid函数的参数
• $\vec x$表示输入层的矢量表示，等价于$\vec a^{[l]}$
• $\vec a^{[l]}$表示序列$l$ (注意从0开始计数) 的神经网络层的输出的矢量表示

使用举例

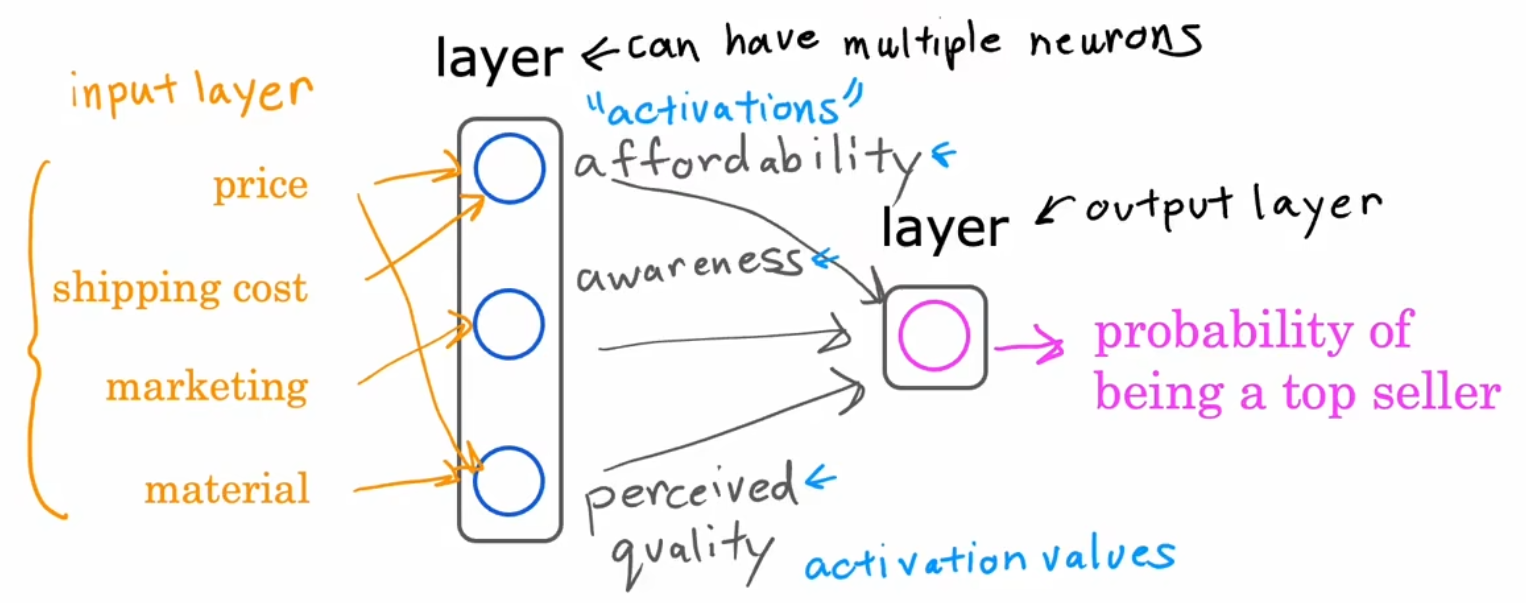
举例 - 需求预测（Demand Prediction）

例如我们要根据价格、运费、促销、材质来预测是否畅销

大概原理如下图，但是不需要手动去设置特征，中间层是自动算的

举例 - 图像感知、物品识别

图像的输入方式

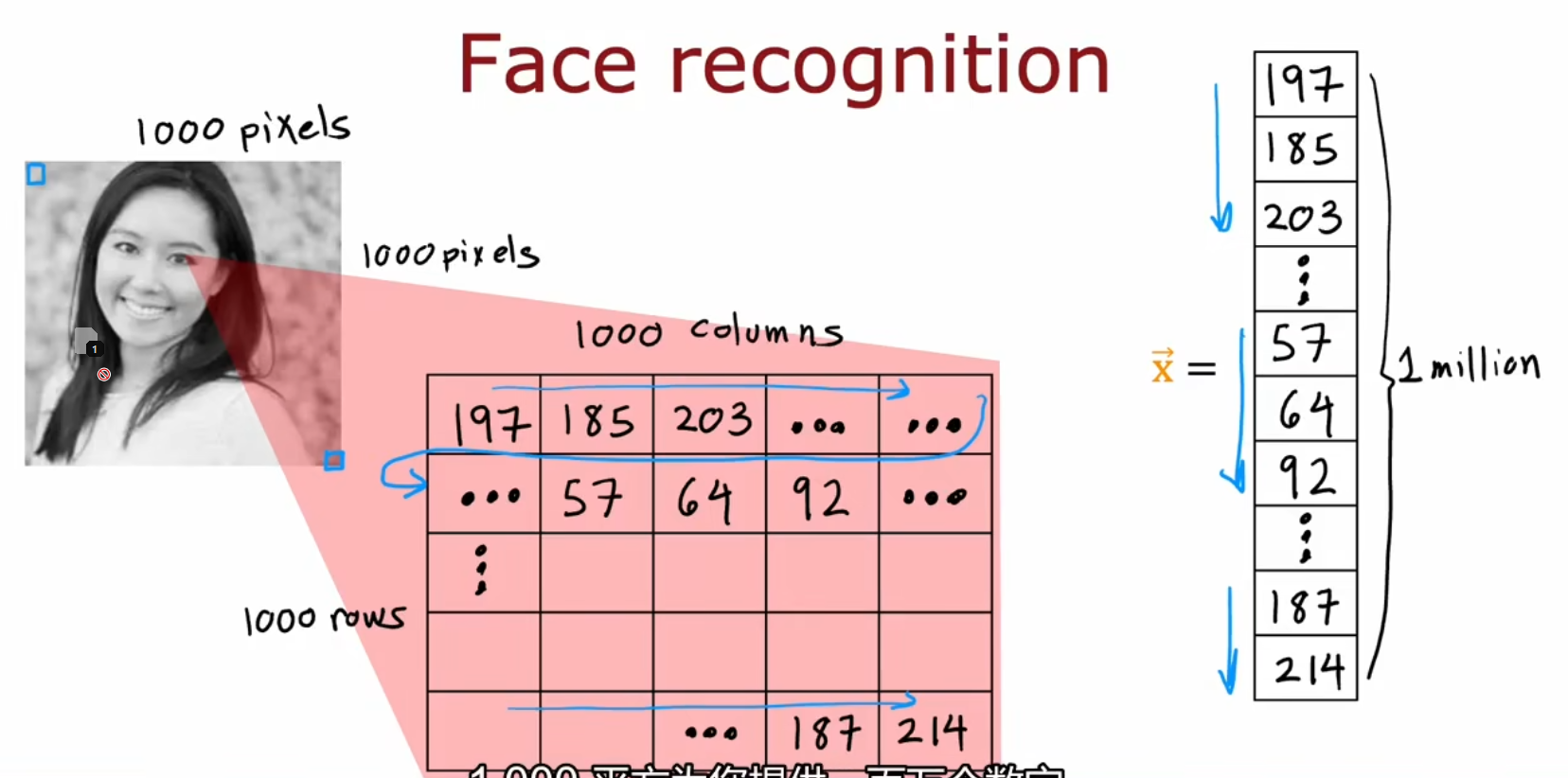
不同层的分工

人脸识别

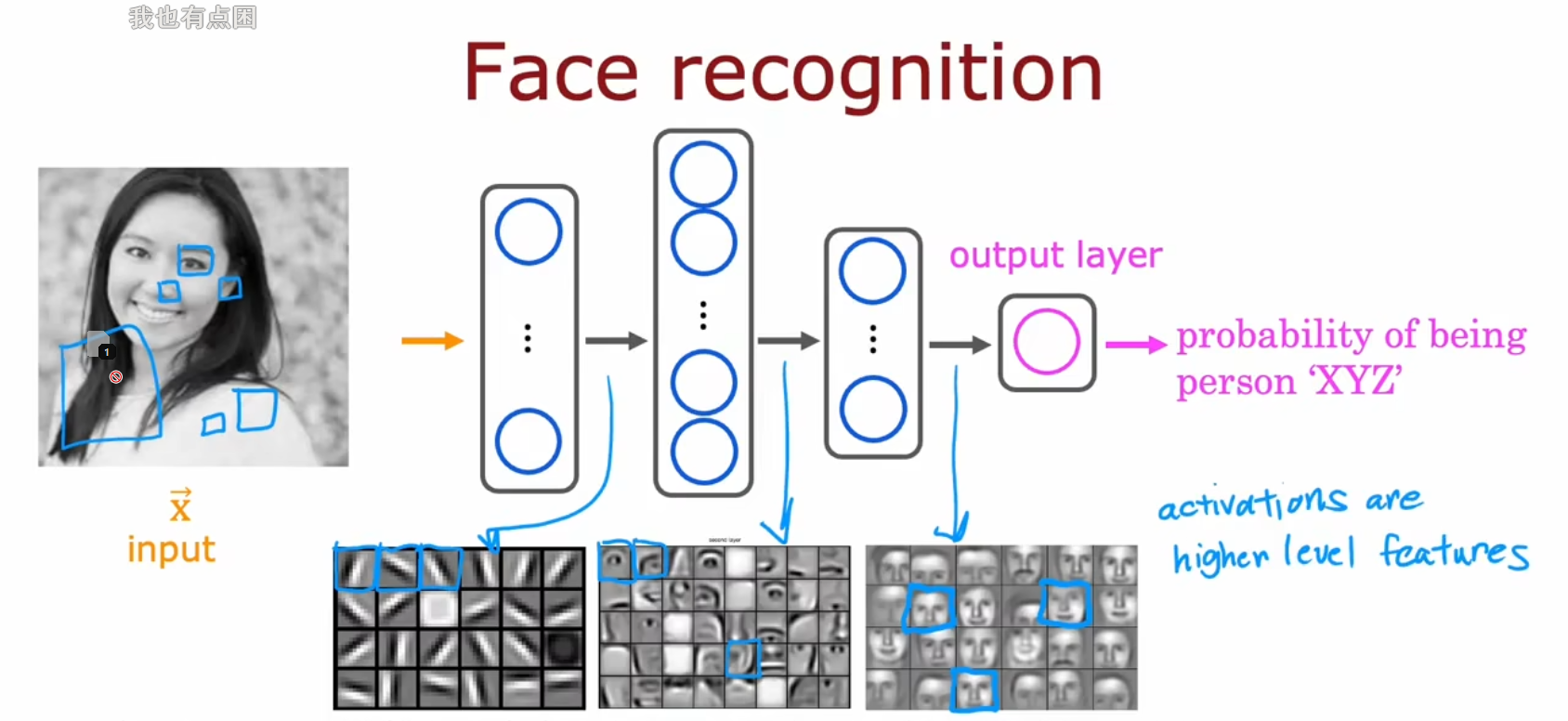
车辆检测

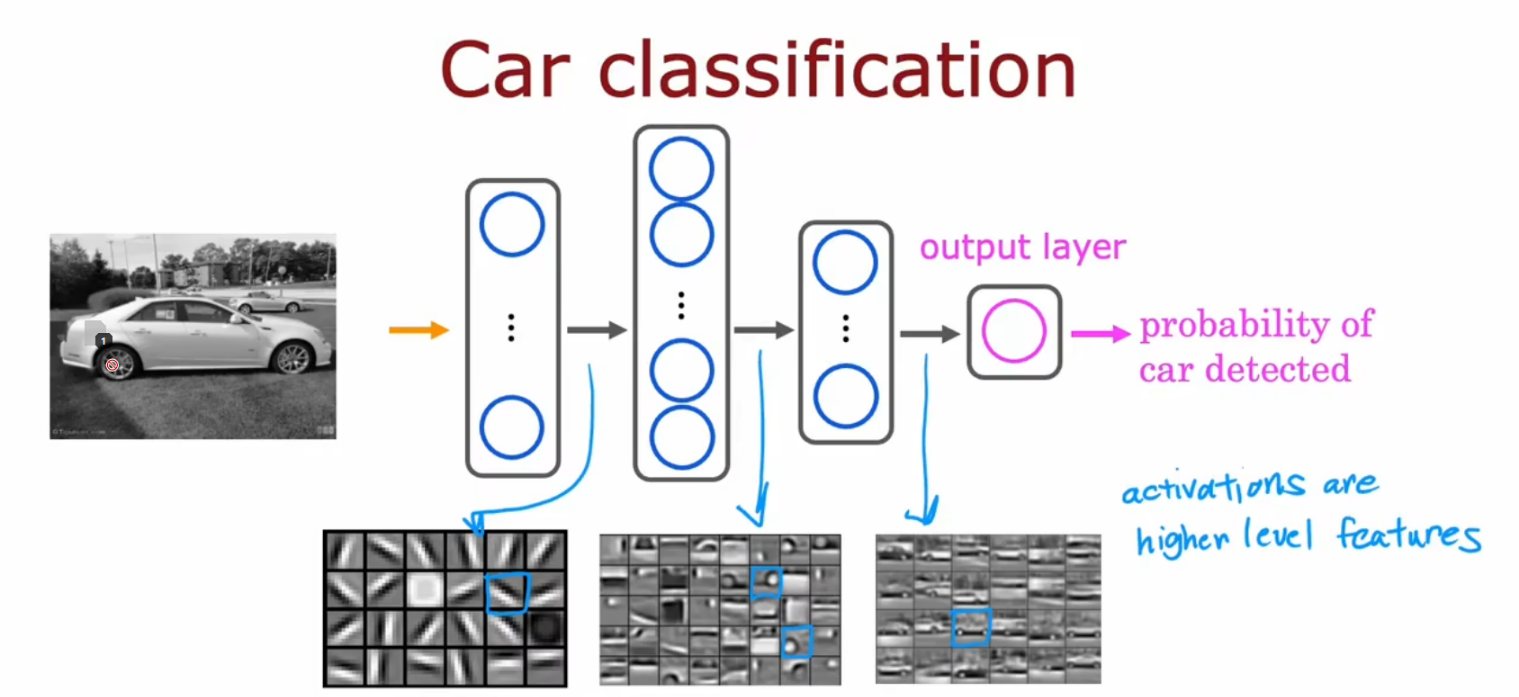
前向传播（Forward Propagation）

另参考：

• 【CSDN】前向传播算法(Forward propagation)与反向传播算法(Back propagation)
• 【知乎】什么是前向传播算法(Forward propagation)？

概念

• 前向传播 / 正向传播（Forward Propagation）算法

  • 简单解释：将上一层的输出作为下一层的输入，并计算下一层的输出，一直到运算到输出层为止

    当你训练完神经网络后，你就可以通过前向传播来用训练后的模型进行预测

  • 其他特性：随着靠近输出层，隐藏层的 Neuron (Units) 数量会减少

• 反向传播（Backward Propagation / Back Propagation）算法

  • 与前向传播相对应

公式

对于前向传播来说，不管维度多高，其过程都可以用如下公式表示：

$$a^2=\sigma(z^2)=\sigma(a^1*W^2+b^2)$$

其中，上标代表层数，星号表示卷积，b表示偏置项bias，σ表示激活函数

例如：单个网络层的前向传播：

代码基础

NumPy中数据的形式

NumPy 存储数据的方式：

x = np.array([		# 这是一个矩阵
    [200.0, 17.0],
    [425.0, 18.5]
])

x  = np.array([		# 这是一个4x2矩阵，即四行两列矩阵
    [0.1, 0.2],
    [0.1, 0.2],
    [0.1, 0.2],
    [0.1, 0.2],
])

Tensorflow中数据形式

这里举一个例子：通过温度和时间来判断咖啡是否煮熟（不会未熟或过熟）

温度	分钟	是否好咖啡
200	17.0	1
425	18.5	0
...	...	...

神经网络前向传播的代码：

x = np.array([[200.0, 17.0]])					# 输入数据x
layer_1 = Dense(units=3, activation='sigmoid')	# 第一层神经网络层，定义该层有三个单元，使用Sigmoid作为激活函数
a1 = layer_1(x)									# 将输入数据x传给layer1得到输出

layer_2 = Dense(units=1, activation='sigmoid')	# （重复，不过单元的数量减少为1）
a2 = layer_1(a1)

关于数据形式的补充：

# x：
# 这里的输入向量x变量，需要是一个NumPy的行矩阵的形式

# a1：
tf.Tensor([[0.2 0.7 0.3]], shape=(1,3), dtype=float32)
# a1.numpy()：
array([[1.4661001, 1.12516, 3.2159438]], dtype=float32)

# a2：
tf.Tensor([[0.8]], shape=(1,1), dtype=float32)
# a2.numpy()：
array([[0.8]], dtype=float32)

代码实现

举例 - 手写体数字识别

前向传播中Units的减少

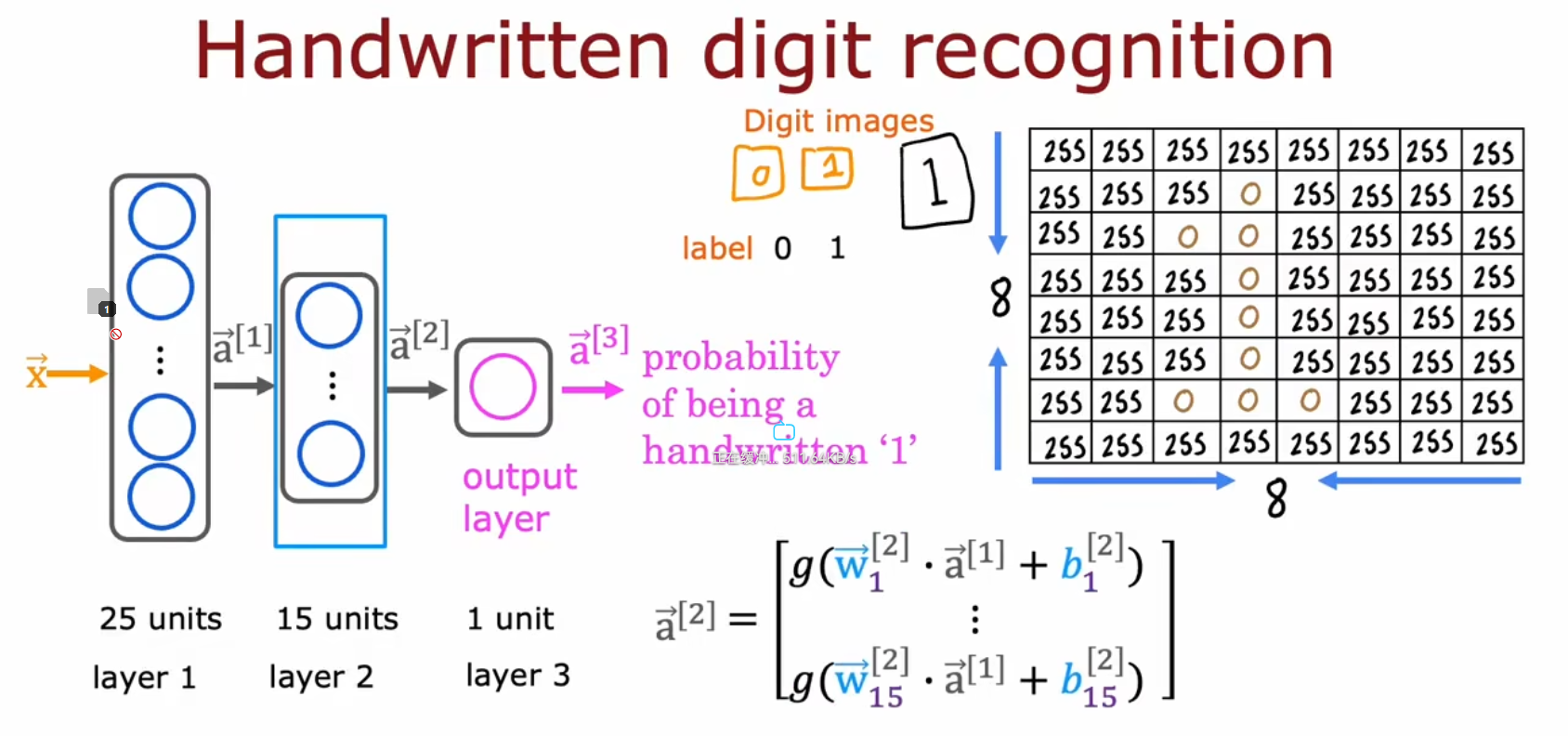
代码

举例 - 判断咖啡是否煮得好

这里举一个例子：通过温度和时间来判断咖啡是否煮熟（不会未熟或过熟）

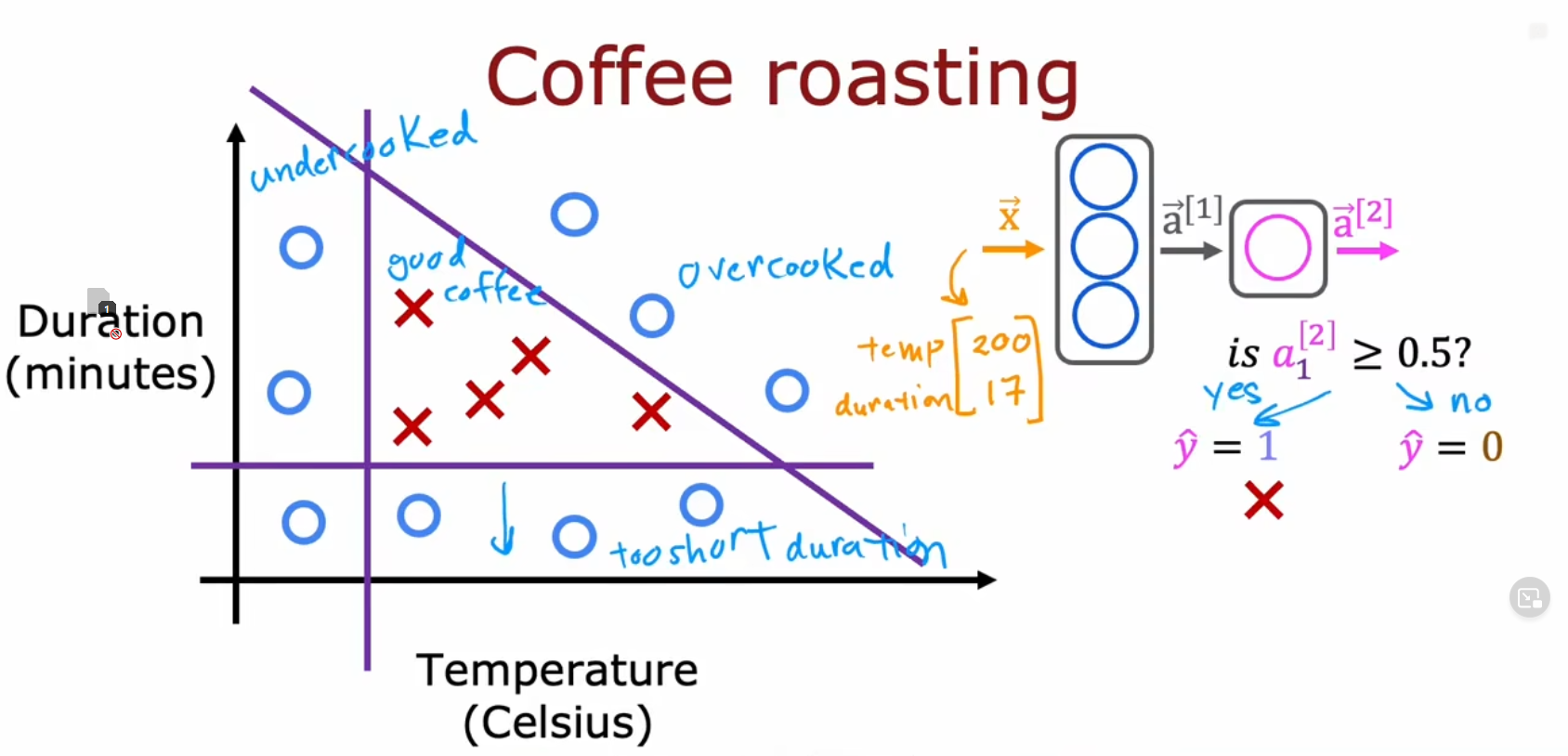
代码：（课程中用的TensorFlow工具）

x = np.array([[200.0, 17.0]])					# 输入数据x
layer_1 = Dense(units=3, activation='sigmoid')	# 第一层神经网络层，定义该层有三个单元，使用Sigmoid作为激活函数
a1 = layer_1(x)									# 将输入数据x传给layer1得到输出

layer_2 = Dense(units=1, activation='sigmoid')	# （重复，不过单元的数量减少为1）
a2 = layer_1(a1)

代码原理

用TensorFlow实现

未矩阵化

W = np.array([
    [1, -3, 5],
    [2, 4, -6]
])
B = np.array([-1, 1, 2])
a_in = np.array([-2, 4])

def dense(a_in, W, B, g="sigmoid"):
    units = W.shape[1]				# shape是[2行,3列]，即 units = 3
    a_out = np.zeros(units)			# a_out = [0,0,0]
    
    for j in range(units):			# 遍历该层的三个神经元，j: 0, 1, 2
        w = W[:,j]					# 获取该神经元的w和b
        b = B[j]					# ^
        z = np.dot(w,a_in) + b		# 通过sigmoid函数计算输出
        a_out[j] = g(z)				# ^
    return a_out

def sequential(x):
    a1 = dense( x, W1, b1)
    a2 = dense(a2, W1, b1)
    a3 = dense(a3, W1, b1)
    a4 = dense(a4, W1, b1)
    f_x = a4
    return f_x

矩阵化

用矩阵运算改良旧代码，矩阵化后最大的优点是可以充分利用 CPU GPU 并行计算的资源，高效快速

def dense(A_in, W, B, g="sigmoid"):
    Z = np.matmul(A_in,W) + B
    A_out = g(Z)
    return A_out

训练（Model Training）

代码实现

代码实现1

还是之前那个判断咖啡是否煮得好的例子

之前是手动一层一层去传播的，现在可以不用

layer_1 = Dense(units=3, activation='sigmoid')	# 定义层
layer_2 = Dense(units=1, activation='sigmoid')
model = Sequential([layout_1, laoyout_2])		# 定义一个神经网络

x = np.array([									# 定义输入矩阵
    [200.0, 17.0],
    [120.0, 5.0],
    [425.0, 20.0],
    [212.0, 18.0]
])
y = np.array([1,0,0,1])							# 定义输出向量（可以看成是列矩阵）

# model.compile(...) # （这个以后再学）
model.fit(x,y)									# 训练模型
model.predict(x_new) 							# 用模型预测新数据

代码实现2

import tensorflow as tf							# tensorflow包
from tensorflow.keras.layers import Dense		# 可以用来创建层
from tensorflow.keras import Sequential			# 可以用多个层来创建神经网络

model = Sequential([
    Dense(units=25, activation='sigmoid'),
    Dense(units=15, activation='sigmoid'),
    Dense(units= 1, activation='sigmoid')
])

from tensorflow.keras.losses import BinaryCrossentropy	# 二进制交叉熵
model.comile(loss=BinaryCrossentropy())			# 定义Loss函数
model.fit(X,Y,epoches=100)						# 训练神经网络，Epoches参数为梯度下降的次数

训练的三个步骤

训练步骤（Model Training Steps）有三个：

① 定义模型、定义层与激活函数

② 定义Loss函数、Cost函数

③ 最优化、模型训练

训练的三个步骤 - 具体

公式中

① 定义模型

公式

$$f_{\vec w,b}(\vec x)=?$$

② 定义Loss函数和Cost函数

公式

$${\color{orange}L(f_{\vec w,b}(\vec x),y)}=?\\ J(\vec w,b)=\frac1m \sum^m_{i=1} {\color{orange}L(f_{\vec w,b}(\vec x_i,y_i))}$$

③ 最优化

公式

$$\text{minimize }J(\vec w,b)$$

---

逻辑回归中

① 定义模型

z = np.dot(w,x) + b
f_x = 1/(1+mp.exp(-z))

② 定义Loss函数和Cost函数

loss = -y * np.log(f_x) - (1-y)*np.log(1-f_x)\\

③ 最优化

...
w = w - alpha * dj_dw
b = b - alpha * dj_dw
...

---

神经网络中

① 定义模型

model = Sequential([
    Dense(...),
    Dense(...),
    Dense(...)
])

② 定义Loss函数和Cost函数

model.compile(loss=BinaryCrossentropy())

③ 最优化

model.fit(X,y,epochs=100)

---

神经网络的优化方法

Model优化 - 正则化

正则化之前介绍过，不再赘述

model = Sequential([
    tf.keras.layers.Dense(units=25, activation='relu',    kernel_regularizer=L2(0.02))
    tf.keras.layers.Dense(units=15, activation='relu',    kernel_regularizer=L2(0.02))
    tf.keras.layers.Dense(units=10, activation='sigmoid', kernel_regularizer=L2(0.02))
])

Optimize优化 - 减少误差

（这章P67 3.4我其实不太看得懂）

先引一个东西：数字舍入误差（numerical roundoff error）

x1 = 2.0/10000
print(f"{x1:.18f}")	# 保留18位小数
# 输出：0.000200000000000000

x2 = 1+(1/10000)-(1-1/10000)
print(f"{x1:.18f}")	# 保留18位小数
# 输出：0.000199999999999978

# 为了减少这些误差，在TensorFlow进行更准确的计算，原理是可以将1/10000看作一个中间量

神经网络中的代码优化如下

# 将
model.compile(loss = SparseCategoricalCrossentropy())
# 替换成
model.compile(loss = SparseCategoricalCrossentropy(from_logits=True))

原理是

$$将\\ \begin{cases} a=g(z)=\frac1{1+e^{-z}}\\ Loss=-y\log (a)-(1-y)\log(1-a)\\ \end{cases}\\ 变成\\ Loss=-y\log (\frac1{1+e^{-z}})-(1-y)\log(1-\frac1{1+e^{-z}})\\$$

Optimize优化 - AdaM优化算法

概念

AdaM算法直觉（AdaM Algorithm Intuition）
其中AdaM含义为：自适应估算方法（AdaM，Adaptive Moment estimation）

我们知道梯度下降法需要设置学习率$\alpha$，学习率过大会导致无法收敛、过小会导致收敛速度太慢。
而该算法能够动态自动调节$\alpha$，刚开始时快速下降，收敛时速度减慢

大概原理

当往一个方向下降时，增大$\alpha_j$。当发现$\alpha$来回正当时，减低$\alpha_j$

代码写法

model = Sequential([
    tf.keras.layers.Dense(units=25, activation='sigmoid')
    tf.keras.layers.Dense(units=15, activation='sigmoid')
    tf.keras.layers.Dense(units=10, activation='linear')
])

model.compile(
    optimizer=tf.keras.optimizers.Adam(learning-rate=1e-3),		 # 指定优化器（使用Adam算法优化，初始学习率为10^-3）
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
)

model.fit(X,Y,epochs=100)