吴恩达机器学习
吴恩达机器学习
目录
决策树(Decision Trees)
决策树模型(Decision Tree Model)
概念
例子:以猫的识别为例(二元分类)
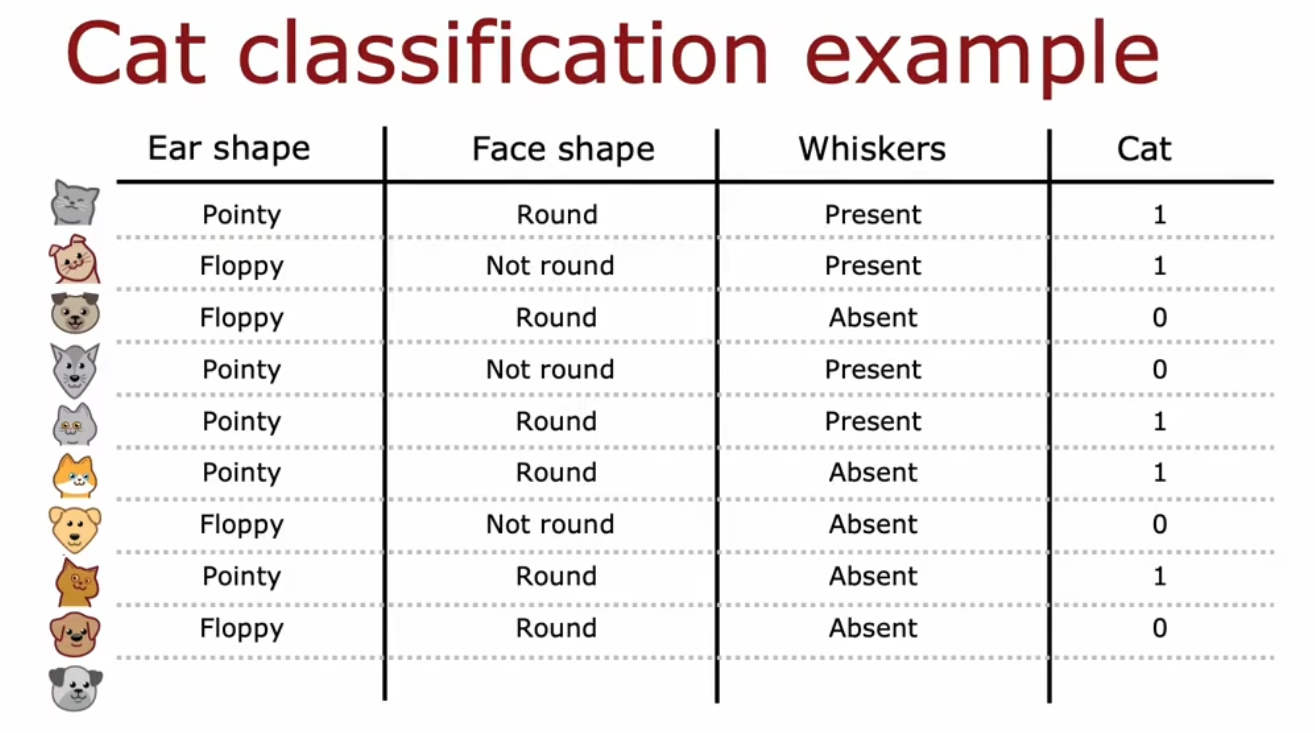
翻译:
- Ear shape 耳朵形状:Pointy 尖的 / Floppy 软的
- Face shape 脸部形状:Round 圆的 / Not round 不是圆的
- Whiskers 胡须:Present 存在 / Absent 不在
- 图中有五只猫和五只狗,1表示是猫
训练后会生成一个树状的东西,叫决策树(Decision Tree)
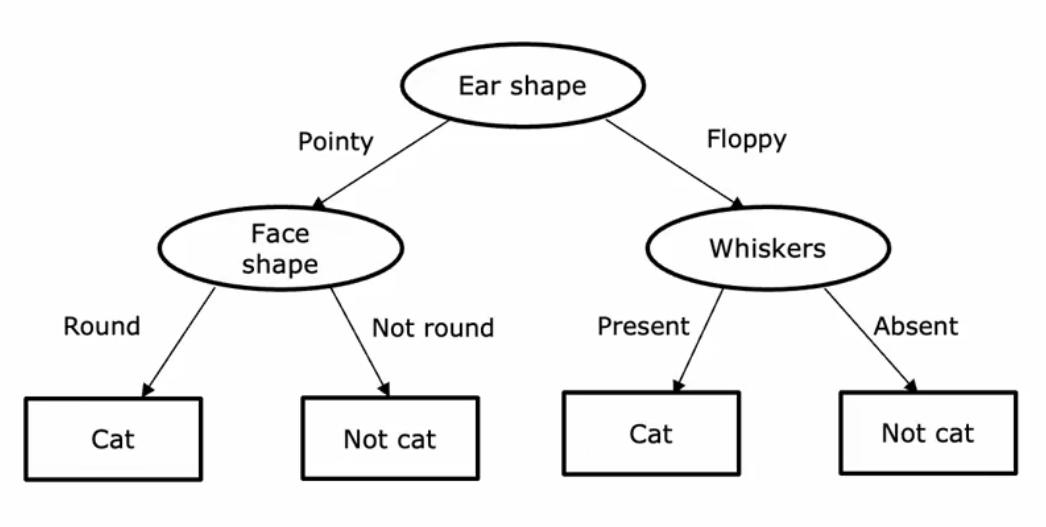
树 tree、枝干 branch、根节点 root、叶子 leaf、二叉树 等概念不再赘述,不知道的话去学数据结构
通过训练可能会生成非常多不同的决策树,我们会选择一个最好的(例如通过交叉验证的方式去选择)
学习过程
如何去学习样本生成决策树?
首先要决定在根节点使用什么特征并按该分类将样本分成两堆,以此类推再决定下一个节点用什么特征,
直到在一个位置,所有样本都是同一种东西,就不用再通过特征分类再分类下去,而是变成叶子节点(Leaf Node)
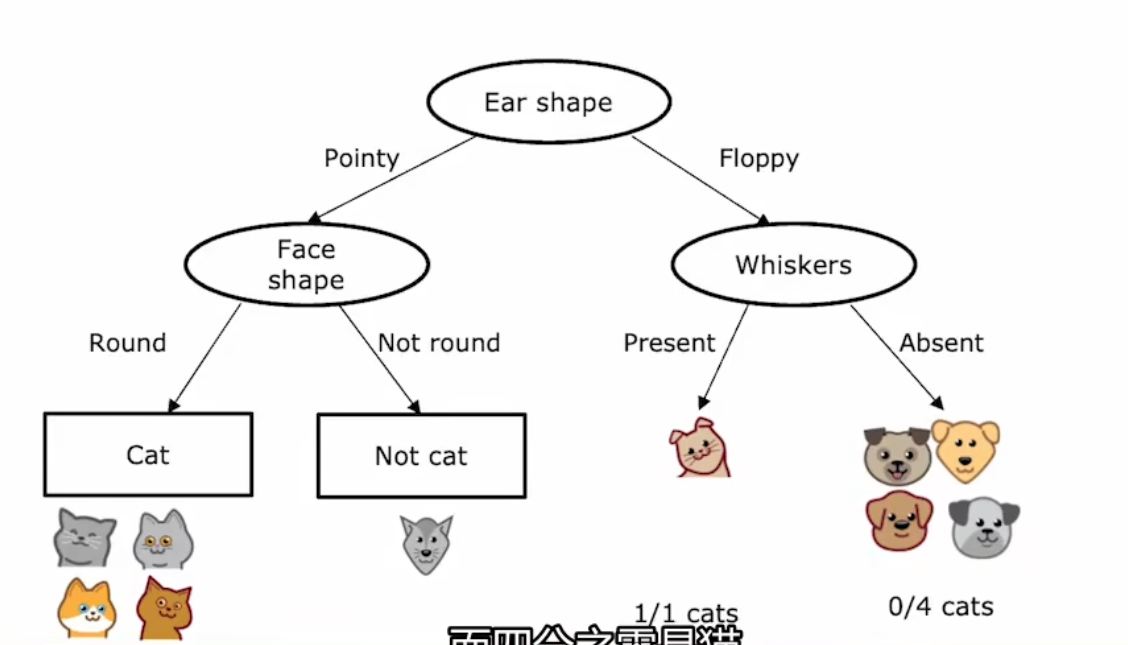
机器学习过程详细步骤
- 从根节点的所有示例开始
- 计算所有可能特征的信息增益,并选择具有最高信息增益的特征
- 根据所选的特征拆分数据集,并创建树的左右分支
- 重复切分过程,直到满足停止条件:
- 当一个节点100%是同一个类
- 当切分一个节点会导致树超过最大深度
- 当信息增益低于阈值(Threshold)
- 当节点中的示例数低于阈值时
拆分原理
拆分诀窍
这里面有一些诀窍
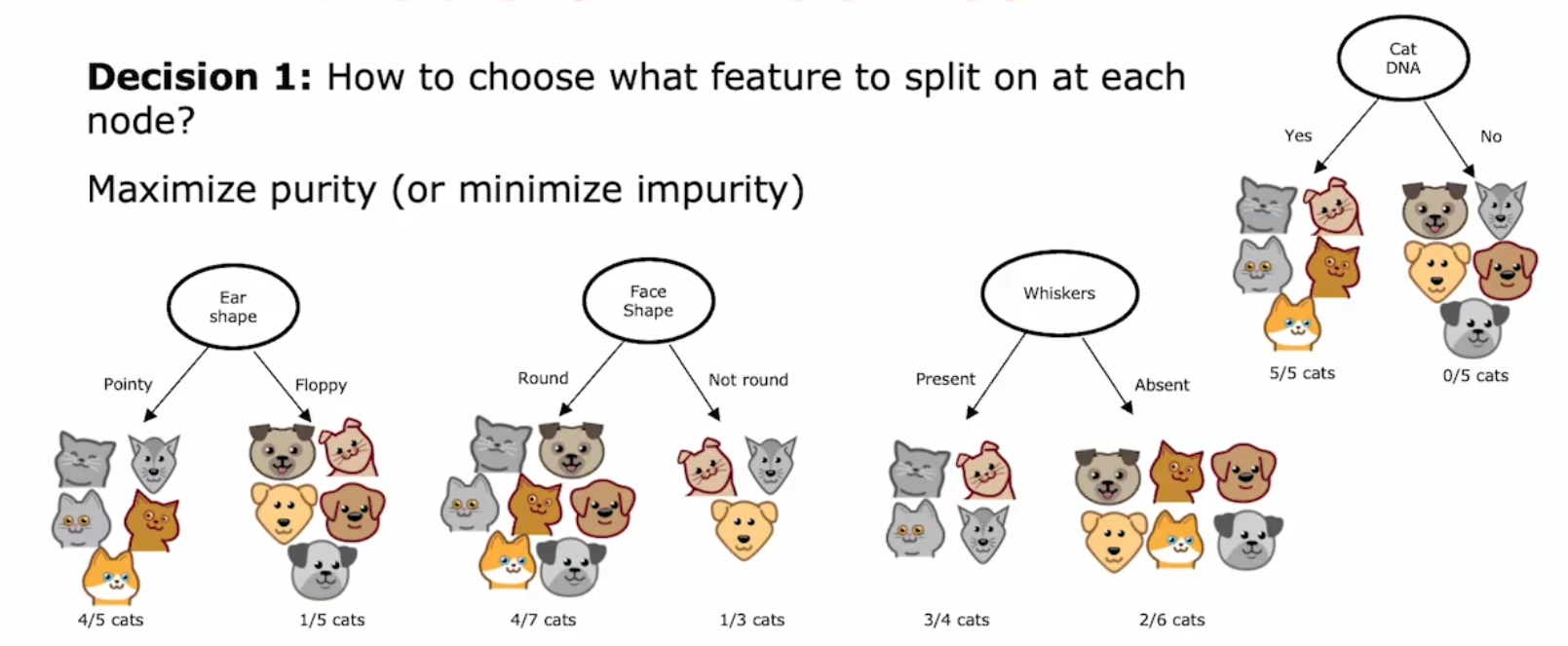
决定1:如何去选择使用哪种特征去开分支?
应该尽可能提高纯度或减低杂质(Maximize Purity / Minimize Impurity)
比如如果一种特征可以直接将猫狗基本分离开,就不要选择另一种特征让左右两支的猫狗依然还是一半一半
该例子中,根节点选择 “Ear Shape” 最佳
决定2:什么时候停止切分(Split)?
- 当节点100%是同一类时
- 当分裂节点时,并且没有结果,将导致树超过最大深度时
(树太大太深则容易过拟合) - 当信息增益度 (熵的减少, 纯度的提高有限时) 低于阈值时
(如果有的狗和猫几乎长得一模一样,那也是没办法的事) - 当节点中的示例数低于阈值时
(比如一条枝干只剩下两三个实例了,你可能不再去切分了)
纯度(Purity)
纯度:Purity,杂志与之相反:Impurity
测量纯度(Measuring purity):熵(Entropy)是杂质(Impurity)的一种度量
公式:
注意
图像
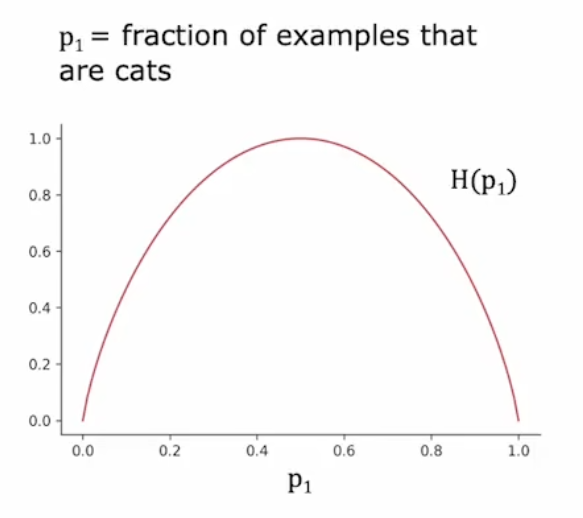
其中
信息增益(Information Fain)
选择拆分:信息增益(Chooing a split: Information Fain)
知道了纯度的概念后,我们需要思考选择什么特征进行切分可以最大程度地减少熵
在决策树学习中,熵的减少称为 信息增益 (Information Fain)
在根节点切分,左右两个分支有产生两个熵值。我们需要结合这两个熵值来判断哪一种切分最好
信息增益公式:
例如下图中,选择信息增益最高的一项 —— 第一项

非二元特征 / 非二元输出
独热编码(One-hot encoding)
应用场景:
之前的例子中,我们总是判断耳朵圆的还是尖的、有没有胡须,这种二元参数来训练。
但如果你的特征有两个以上的离散值,则需要用到 独热编码(One-hot encoding)
定义:
独热编码(One-hot encoding):如果一个分类用特征可以取k个值(可取多个离散值的特征),那么可以创建k个二元特征(这些特征的值只能取0或1)
例如:
| 序号 | 耳朵形状 (x1) | 脸的形状 (x2) | 是否是猫 (y) |
|---|---|---|---|
| 1 | 尖的 | 圆的 | 1 |
| 2 | 椭圆的 | 不是圆的 | 1 |
| 3 | 椭圆的 | 圆的 | 0 |
| 4 | 尖的 | 不是圆的 | 0 |
| 5 | 椭圆的 | 圆的 | 1 |
| 6 | 尖的 | 圆的 | 1 |
| 7 | 下耷的 | 不是圆的 | 0 |
| 8 | 椭圆的 | 圆的 | 1 |
| 9 | 下耷的 | 圆的 | 0 |
| 10 | 下耷的 | 圆的 | 0 |
变成
| 序号 | 是否尖耳 | 是否圆耳 | 是否耷耳 | 脸的形状 | 是否是猫 |
|---|---|---|---|---|---|
| …… | …… (1/0) | …… (1/0) | …… (1/0) | …… (1/0) | …… (1/0) |
通过独热编码,我们能删除该 “猫耳形状” 的特征并建立三个新的特征。做到树转二叉树
接下来的操作就和普通的决策树训练一样了
可取连续值的特征
如果你的特制,可以选择任意连续的数字
例如:
| 序号 | 耳朵形状 | 脸的形状 | 胡须 | 体重 (磅) | 是否是猫 |
|---|---|---|---|---|---|
| 1 | 尖的 | 圆的 | 存在 | 7.2 | 1 |
| 2 | 椭圆的 | 不是圆的 | 存在 | 8.8 | 1 |
| 3 | 椭圆的 | 圆的 | 不存在 | 15 | 0 |
| 4 | 尖的 | 不是圆的 | 存在 | 9.2 | 0 |
| 5 | 尖的 | 圆的 | 存在 | 8.4 | 1 |
| 6 | 尖的 | 圆的 | 不存在 | 7.6 | 1 |
| 7 | 椭圆的 | 不是圆的 | 不存在 | 11 | 0 |
| 8 | 尖的 | 圆的 | 不存在 | 10.2 | 1 |
| 9 | 椭圆的 | 圆的 | 不存在 | 18 | 0 |
| 10 | 椭圆的 | 圆的 | 不存在 | 20 | 0 |
其实万变不离其宗,目的一样,是找到令信息增量最大化的切分方式
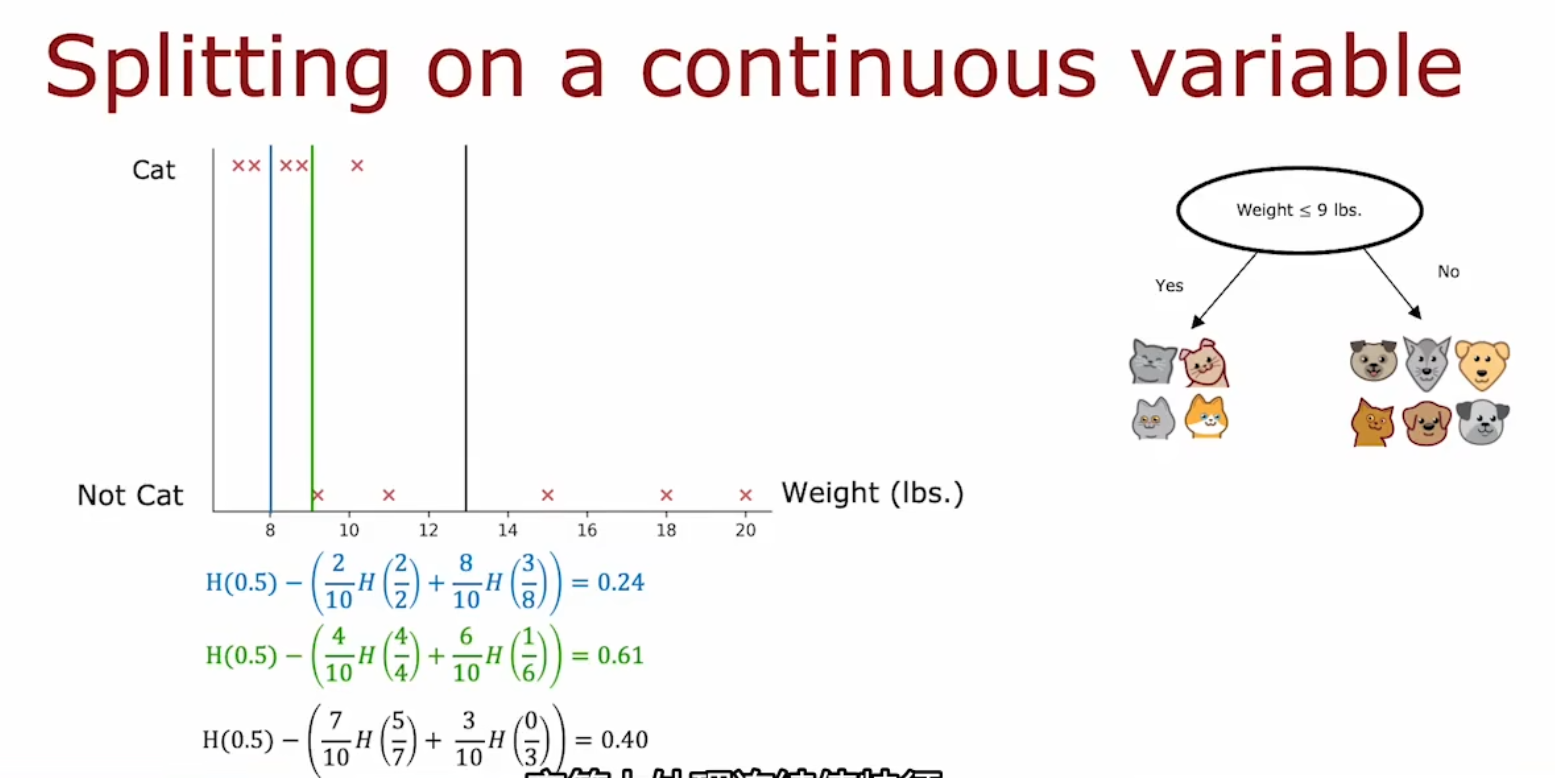
回归树(Regression Trees)(可选章节)
回归树(Regression Trees),或者 回归决策树(Regression with Decision Trees)
训练集:
例如,我们要用前面的特征来预测体重是多少,而不是预测是否是猫
| 序号 | 耳朵形状 | 脸的形状 | 胡须 | 体重 (磅) |
|---|---|---|---|---|
| 1 | 尖的 | 圆的 | 存在 | 7.2 |
| 2 | 椭圆的 | 不是圆的 | 存在 | 8.8 |
| 3 | 椭圆的 | 圆的 | 不存在 | 15 |
| 4 | 尖的 | 不是圆的 | 存在 | 9.2 |
| 5 | 尖的 | 圆的 | 存在 | 8.4 |
| 6 | 尖的 | 圆的 | 不存在 | 7.6 |
| 7 | 椭圆的 | 不是圆的 | 不存在 | 11 |
| 8 | 尖的 | 圆的 | 不存在 | 10.2 |
| 9 | 椭圆的 | 圆的 | 不存在 | 18 |
| 10 | 椭圆的 | 圆的 | 不存在 | 20 |
训练后的模型:
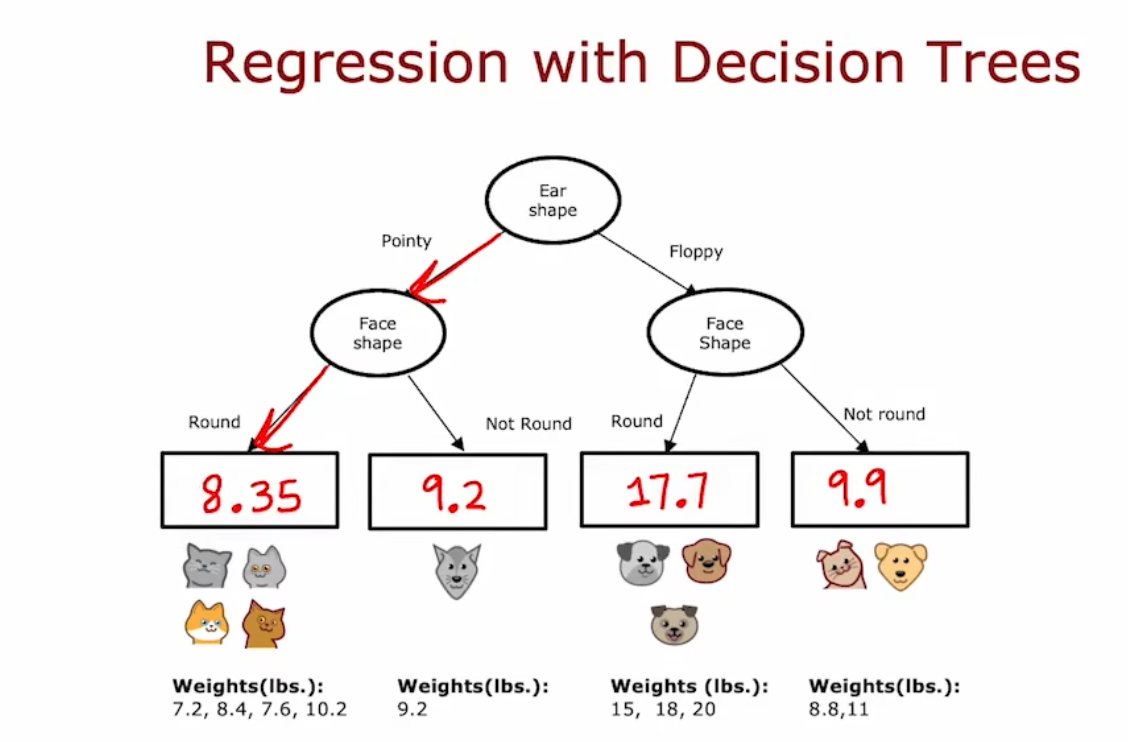
问题在于,如何选择切分方式?以使信息增益最大
计算上,这次不是计算熵的减少幅度,而是计算方差的减少幅度,方差减少幅度越大则信息增益越大
公式:
该例子中:选择第一个切分方式

树系(Tree Ensemble)
树系
注意这里的英语应该是 **Tree Assemble(树系)**而不是 Tree ensemble(树集合)
应用场景:
使用单个决策树的缺点之一,是微小变化高度敏感。
使其不那么敏感或更健壮的一种解决方案是,构建和使用多个决策树(Using multiple decision trees),
即构建 树系(Tree Ensemble)
例如:
这里我们仅仅在训练集中更改一个示例,就会导致决策树完全不同(从根的切分开始就不同了),算法不那么健壮

我们可以构建多个决策树,变成一个树系。不同的决策树的预测结果可能不同,我们让他们投票。根据票数得到最终结论
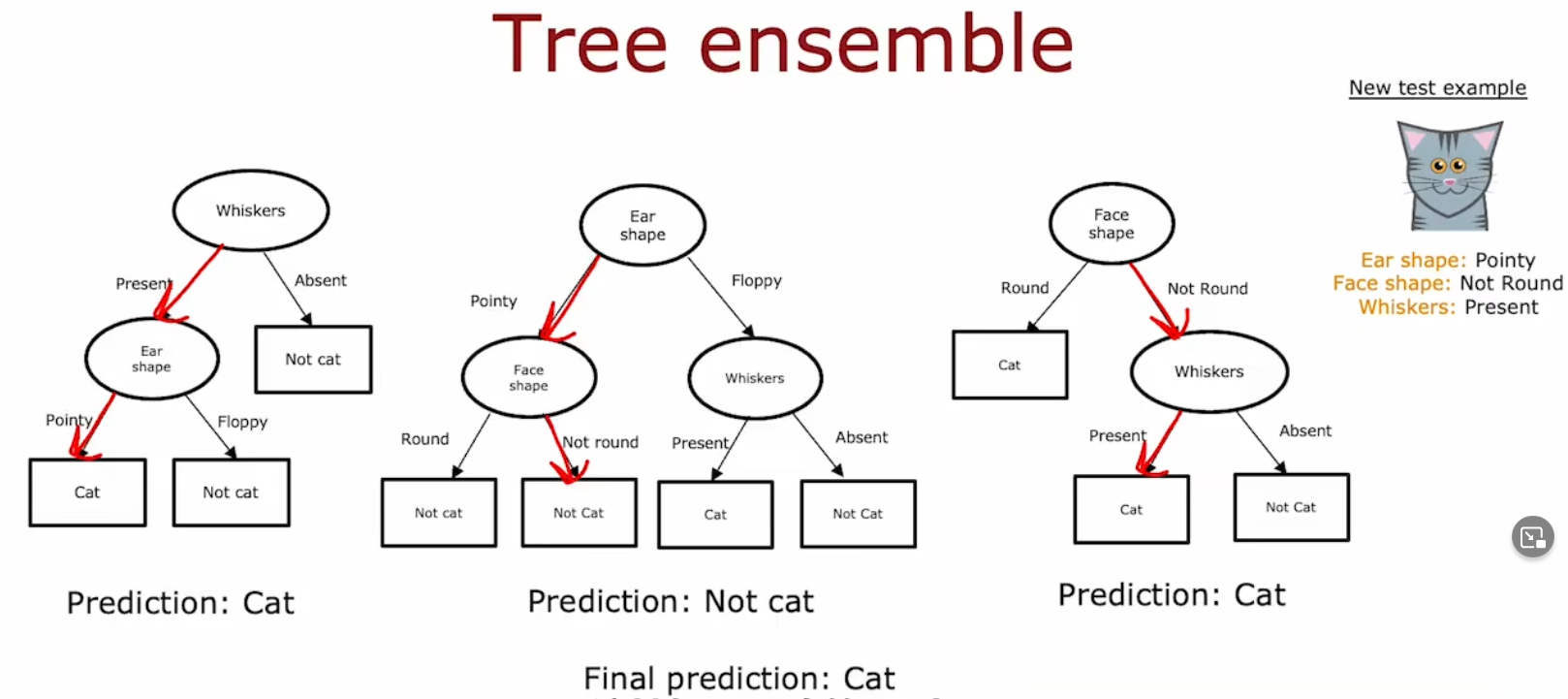
有放回抽样(Sampling with replacement)
有放回抽样(Sampling with replacement)和 无放回抽样(Sampling without replacement)
两者的区别学过高中课的都懂,不再赘述
其中 Replacement 也有替换的意思
这个概念怎么用?
构建多个随机训练集(Multiple random training sets),这和原来旧的训练集不同
新的训练集可以用来构建树系
随机森林(Random Forest)
随机森林算法(Random forest algorithm),它是一种强大的树
反向决策树(Back Decision Tree)?(翻译问题?)
做法
给定一个大小为m的训练集,那么
使用有放回抽样来创建一个新的大小为m的训练集,然后在此数据集上训练决策树
重复这个过程B次,生成多个决策树
(B值的设置:设置更大则更精确。但超过某个点时收益递减,反而会显著减慢计算速度。一般B远大于100时没什么意义)决策时,让这些树进行投票
改进做法
对于大部分情况来说,上面这些决策树会是相似甚至相同的,每个节点切分所选择的特征会是一样的
我们需要对算法进行一项修改,以进一步随机化每个节点切分的特征选择在每个节点上,当选择用于拆分的特征时。
如果有n个可用的特征,从 k<n 个特征中随机选择一个子集,并允许算法只从这个特征子集中进行选择
一般我们会选择
(典型值而已,像西瓜书里取的是。值根据经验来的,没什么特别含义)
虚拟包(Virtual Bag)?
不知道什么东西
XGBoost(eXtreme Gradient Boosting,极端的梯度增加)
XGBoost
定义
- 一种比随机森林更优的算法,一种增强决策树算法(boosted decision tree)
一些特点
增强树的开源实现
快速高效的实现
不错的默认拆分标准和何时停止拆分的标准选择
内置正则化以防止过拟合
用于机器学习竞赛的高竞争性算法(例如: Kaggle竞赛)
思想原理
刻意学习(deliberate pracitice):比如你练钢琴,有一小段练不好。你可以集中去练习那一段,而不是每一次都练习整首曲子。特别那一段不好的部分在曲子中的占比很低,如果每次都练整首曲子将会非常耗时。
训练决策树也是同理,我们可以去关注做得差的部分,去获得新的决策树,尝试把这部分做好。这就是 Boosting 的想法
每一次,误判的项会有更高的概率被抽取
代码 - 分类
from xgboost import XGBClassifier
model = XGBClassifier() # XGBoost-分类器
model.fit(X_train, y_train)
y_pred = model.predict(X_test)代码 - 回归
from xgboost import XGBClassifier
model = XGBRegressor() # XGBoost-回归器
model.fit(X_train, y_train)
y_pred = model.predict(X_test)决策树 vs 神经网络
决策树和神经网络的选用
各自的优缺点:
决策树和树系(Decision Trees & Tree Ensembles)
- 能很好地处理表格 (结构化) 数据
但不建议用于非结构化数据 (图像、音频、文本) - 快
- 小型决策树可能是人类可以理解的 (但被夸大,大多数情况都是大型的)
神经网络(Neural Networks)
- 能很好地处理所有类型的数据,包括表格 (结构化) 和非结构化数据
- 比决策树慢
- 可以迁移学习
- 当建立一个由多个模型共同工作的系统时,把多个神经网络串在一起可能更容易