吴恩达机器学习
目录
强化学习(Reinforcement Learning)
什么是强化学习
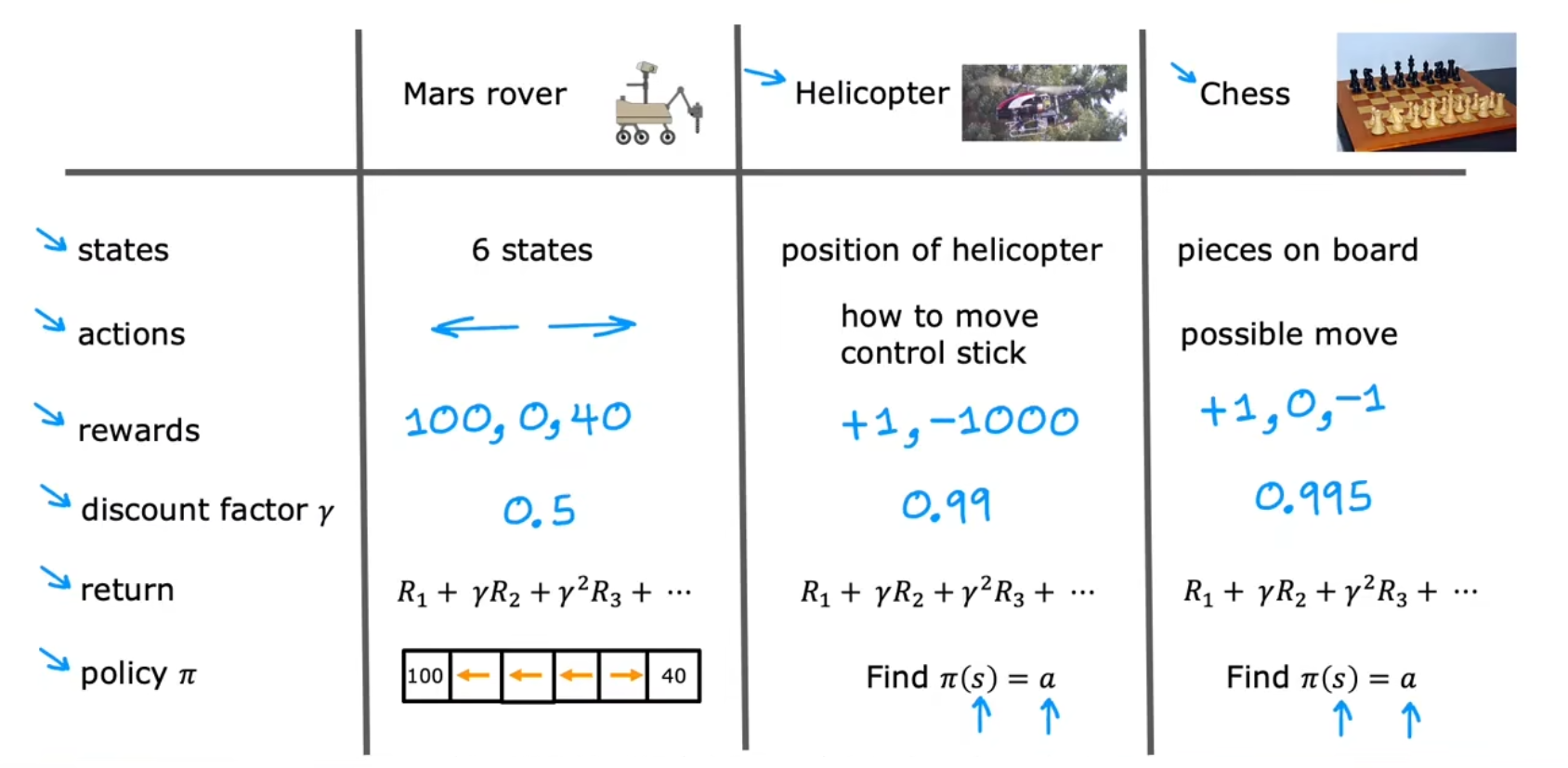
应用,例如:无人驾驶直升机
直升机的位置 --> 如何移动控制杆
状态 s --> 行动 a
x --> y
奖励函数
- 积极回报:当直升机飞得好时
- 消极回报:当直升机飞得不好
应用
- 控制机器人
- 工厂优化
- 金融 (股票) 交易
- 玩游戏 (包括电视游戏)
强化学习的限制
- 在模拟中工作要比真正的机器人容易得多
- 比监督和非监督学习的应用要少得多
- 但是……具有未来应用潜力的令人兴奋的研究方向
实例:火星探测器(Mars rover)
火星探测器的例子
比如往左3格,可以采样一份研究价值为100的土壤,往右2格,则可以采样一份研究价值为40的土壤。这时应该怎么决策?
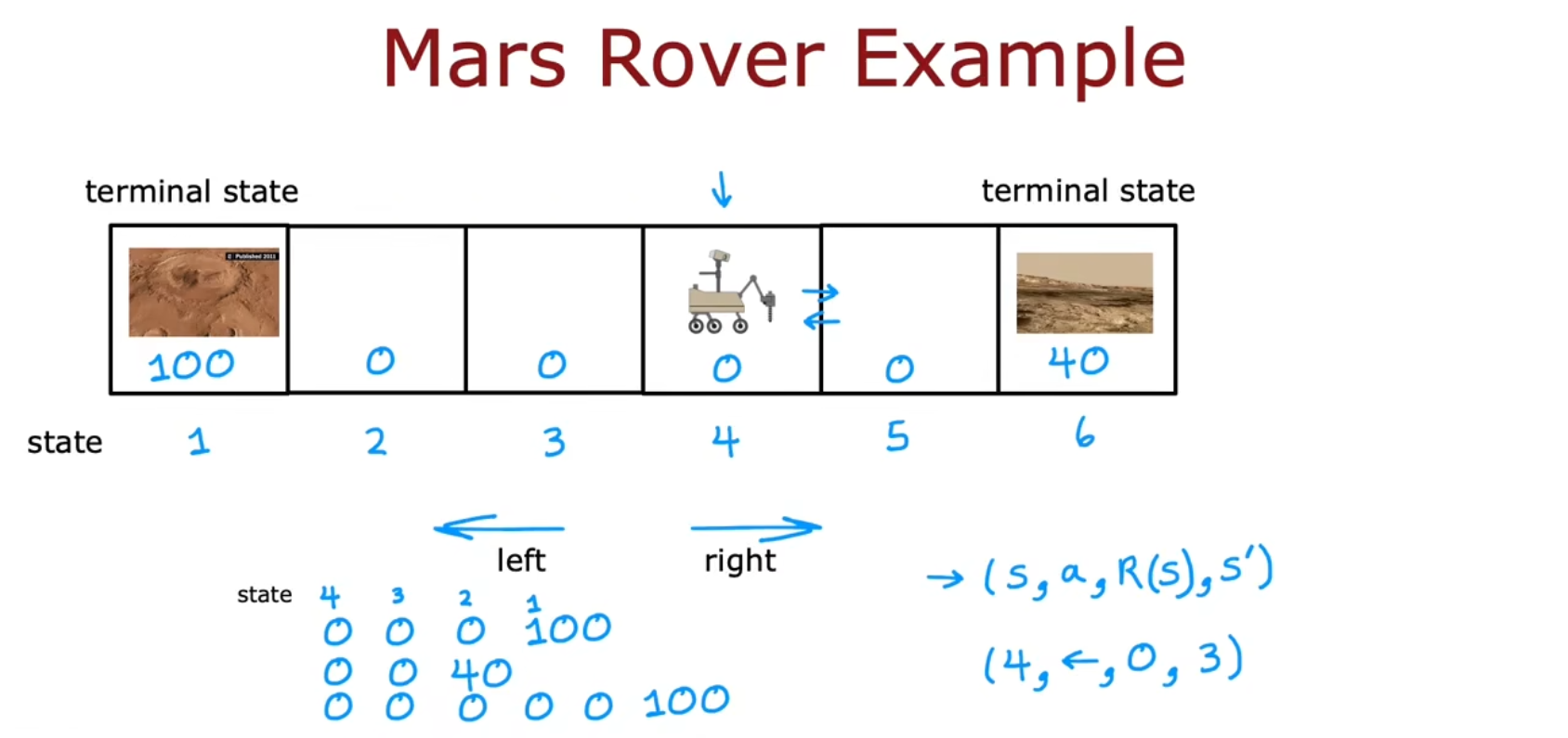
一些术语
一些术语:
| 术语 (中) | 术语 (英) | 符号 | 补充 |
|---|
| 状态 | State | s | 当前状态,例如火星车的位置在强化学习中称为状态,六个位置即六种状态 |
| 动作 | Action | a | |
| 奖励函数 | Reward function | R(s) | |
| 回报 | Return | Return | 奖励的综合(Sum of rewards)。Return=R1+γR2+γ2R3+⋯ |
| 折扣系数 | Discount factor | γ | 取值0~1,用于幂后加权。类似于:利率或货币的时间价值 |
| 策略 | Policy | π(s) | 策略函数 |
| 状态动作价值函数 | State Action value function
/ Q-function | Q(s,a) | 状态-动作价值函数,也叫 Q-function |
一些符号:
- s:当前状态
- a:当前动作
- R(s):当前状态的奖励
- s′:行动a后的状态
- a′:状态s′所对应的行动
状态 s、动作 a、奖励 R(s)
状态 动作 奖励 的表示:(s,a,R(s),s′)

回报、折扣系数 γ
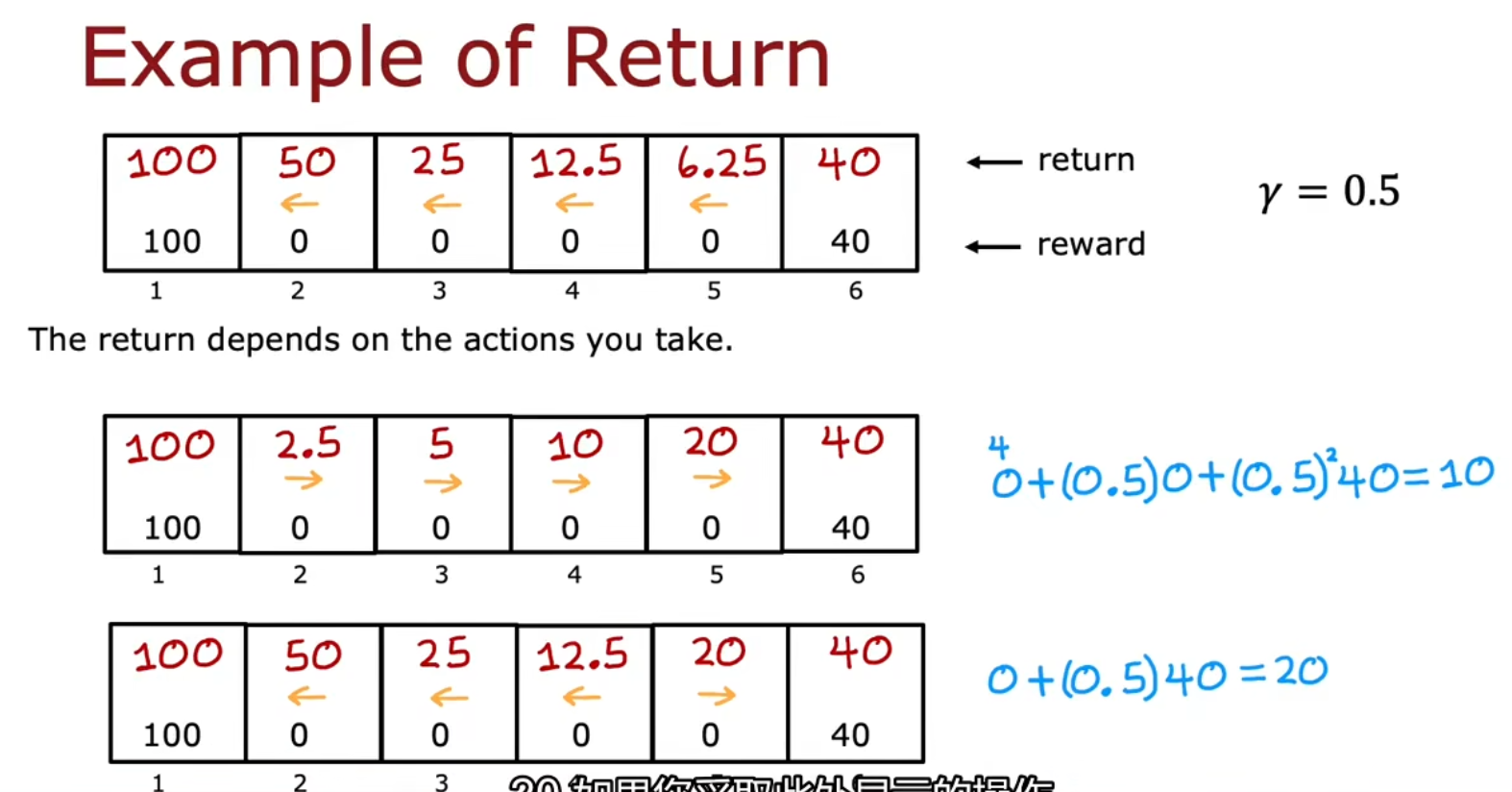
回报的计算方式:

如果γ较大,那基本是利益优先。若γ较小,则会更倾向于去近一点的地方
当γ=0.5,且位于状态4时,往左是更佳的决策
当γ=0.3,且位于状态4时,往右是更佳的决策
策略 π(s)
决策:强化学习中的策略
我们提出一个策略(Policy),我们希望这个策略能基于状态告诉我们应该干什么
π(s)=aπ(2)=←π(3)=←π(4)=←π(5)=→
状态动作价值函数 Q(s,a)
英文:State Action value function,因为常用符号Q(s,a)表示,也叫 Q-function
比如Q(2,→)中,策略为往右一格再往左两格,分数为12.5

其他
其他例子
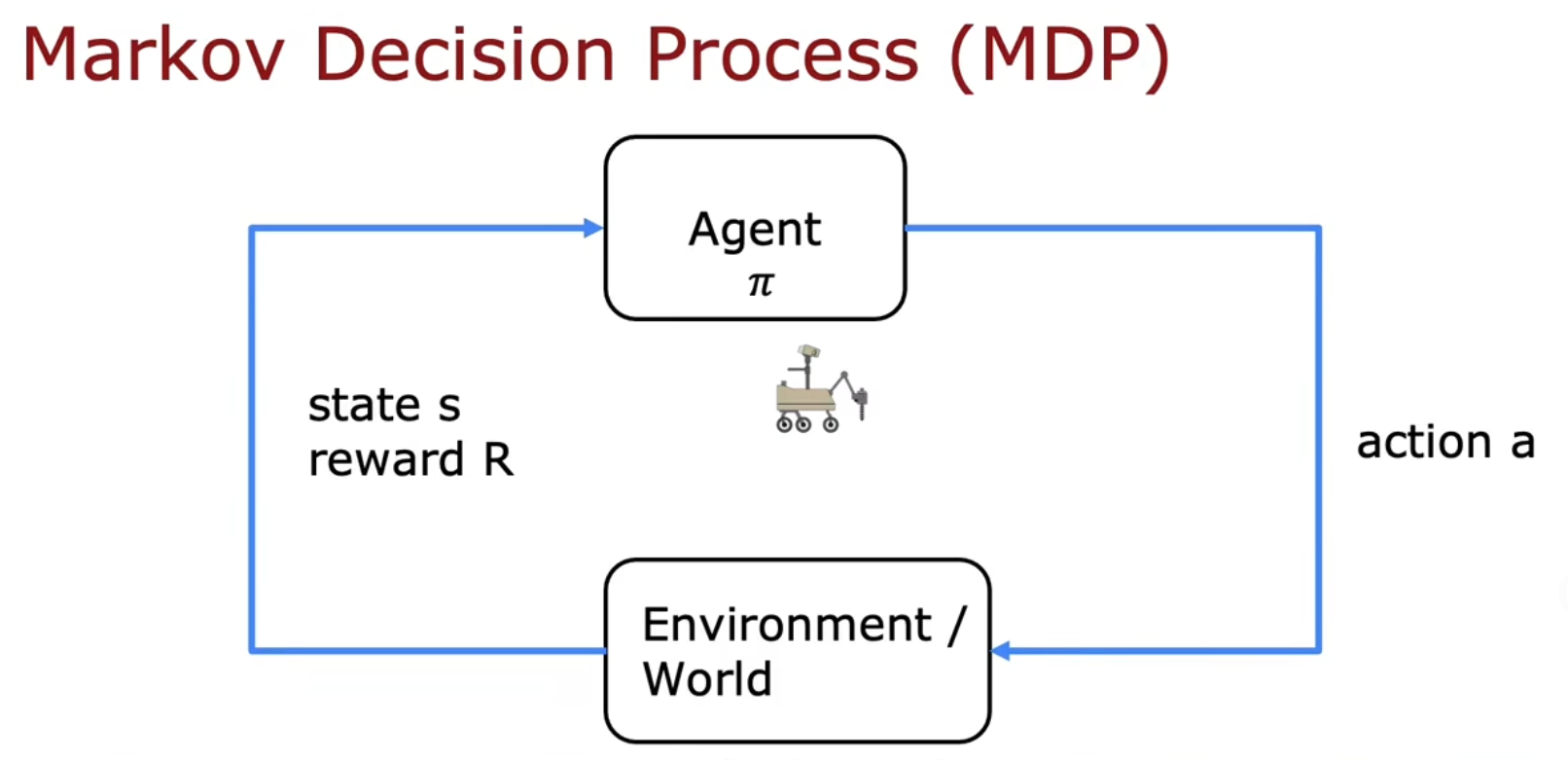
马尔科夫决策过程(MDP,Markov Decision Process)
应该就是 马尔科夫链 的那个 马尔科夫
贝尔曼方程(Bellman Equation)
如何计算 状态动作价值函数?
复习一下符号:
- s:当前状态
- a:当前动作
- R(s):当前状态的奖励
- s′:行动a后的状态
- a′:状态s′所对应的行动
贝尔曼方程:是一个递归方程
Q(s,a)=R(s)+γa′maxQ(s′,a′) 例如:Q(2,→)==R(2)+0.5a′maxQ(3,a′)0+0.5∗25=12.5 推导原理:R1+γR2+γ2R3+γ3R4+⋯=R1+γ[R2+γR3+γ2R4+⋯]
随机环境(Random (/Stochastic) Environment)(可选)
Random (/Stochastic) Environment(随机环境)
依然是火星车的例子:
假如你让它向左走,有90%的概率向左走,有10%的概率向右走
假如你让它向右走,有90%的概率向右走,有10%的概率向左走
回报期望 & 贝尔曼方程:
回报期望 Expected Return== 贝尔曼方程:Q(s,a)=Average(R1+γR2+γ2R3+γ3R4+⋯)E [R1+γR2+γ2R3+γ3R4+⋯]R(s)+γ E [a′maxQ(s′,a′)]
连续状态空间(Continuous state)
示例 - 连续状态空间应用
之前的例子中,火星车的状态只有六种离散状态。这节将会将它的状态延伸为连续的状态空间
比如车子的位置和朝向的表示:
s=xyθx˙y˙θ˙
比如直升机,还有多了一个方向的位移和两个方向上的旋转
s=xyzϕθωx˙y˙z˙ϕ˙θ˙ω˙
实例:登月器(Lunar Lander)
例子
登月器着陆
s=xyx˙y˙θθ˙lrl:左脚是否着地,r:右脚是否着地
登月器奖励的设置,例如
- 到达着陆点:100-140
- 向/远离 垫 移动的额外奖励
- 坠毁:-100
- 软着陆:+100
- 腿被禁足:+10
- 消防主机:-0.3
- 消防侧推进器:-0.03
对于登月器来说γ的值挺大的,例如设置γ=0.985
DQN算法(Deep Q-Network)/ 状态值函数(State-value function)
学习 状态值函数(Learning the state-value function),该算法也叫 DQN算法(Deep Q-Network)
用神经网络训练模型来学习Q函数
如何训练强化学习的神经网络?
x=y==≈y(1)=Qnew(s,a)≈(s,a)Q(s,a)R(s)+γa′maxQ(s′,a′)?fW,B(x)R(s(1))+γa′maxQ(s′(1),a′)y (s,a,R(s),s′)(s(1),a(1),R(s(1)),s′(1))
重放缓冲区(Replay Buffer)
训练:创建1w个示例,用于训练
x=(s,a)y=R(s)+γa′maxQ(s′,a′)
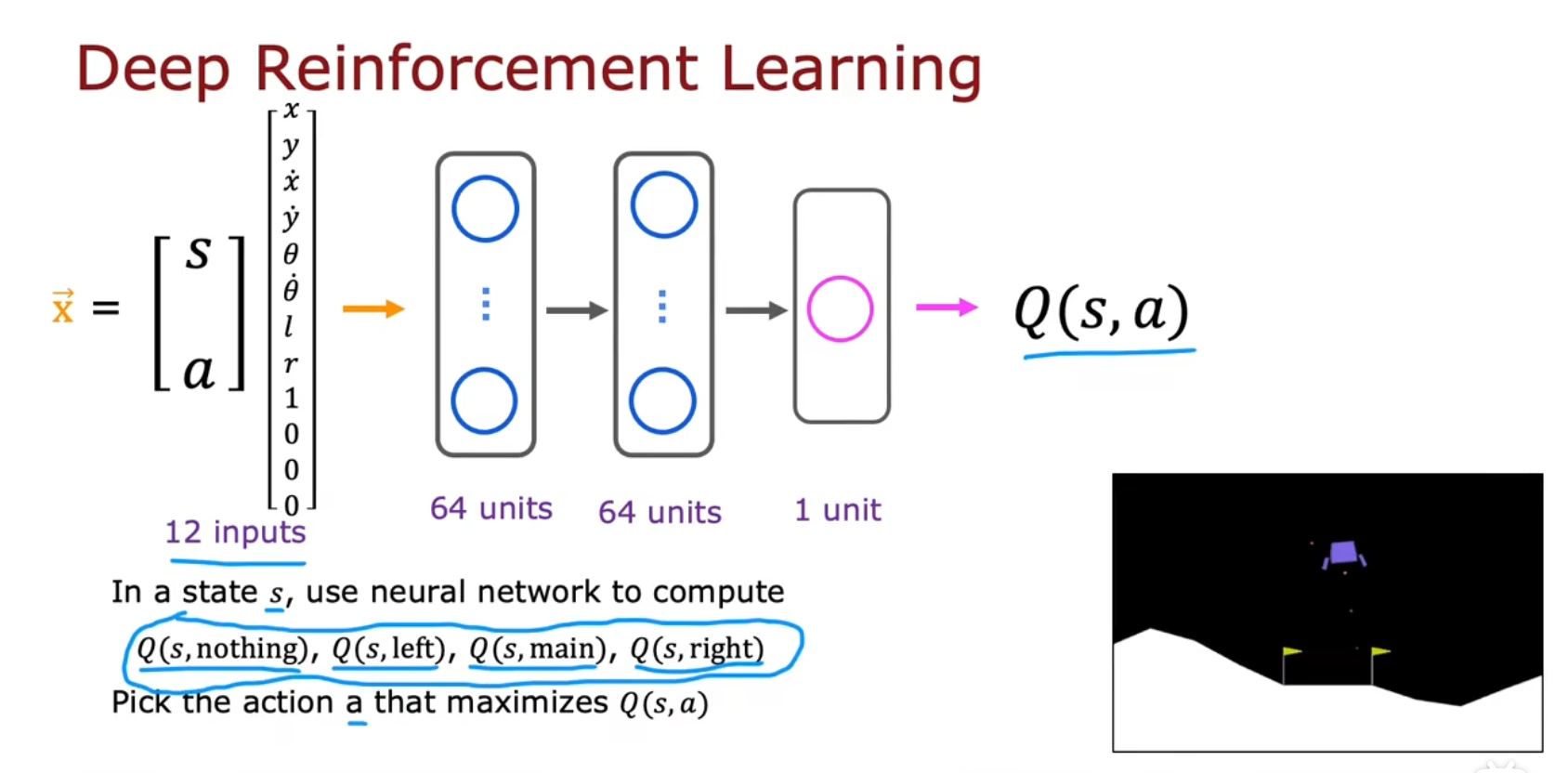
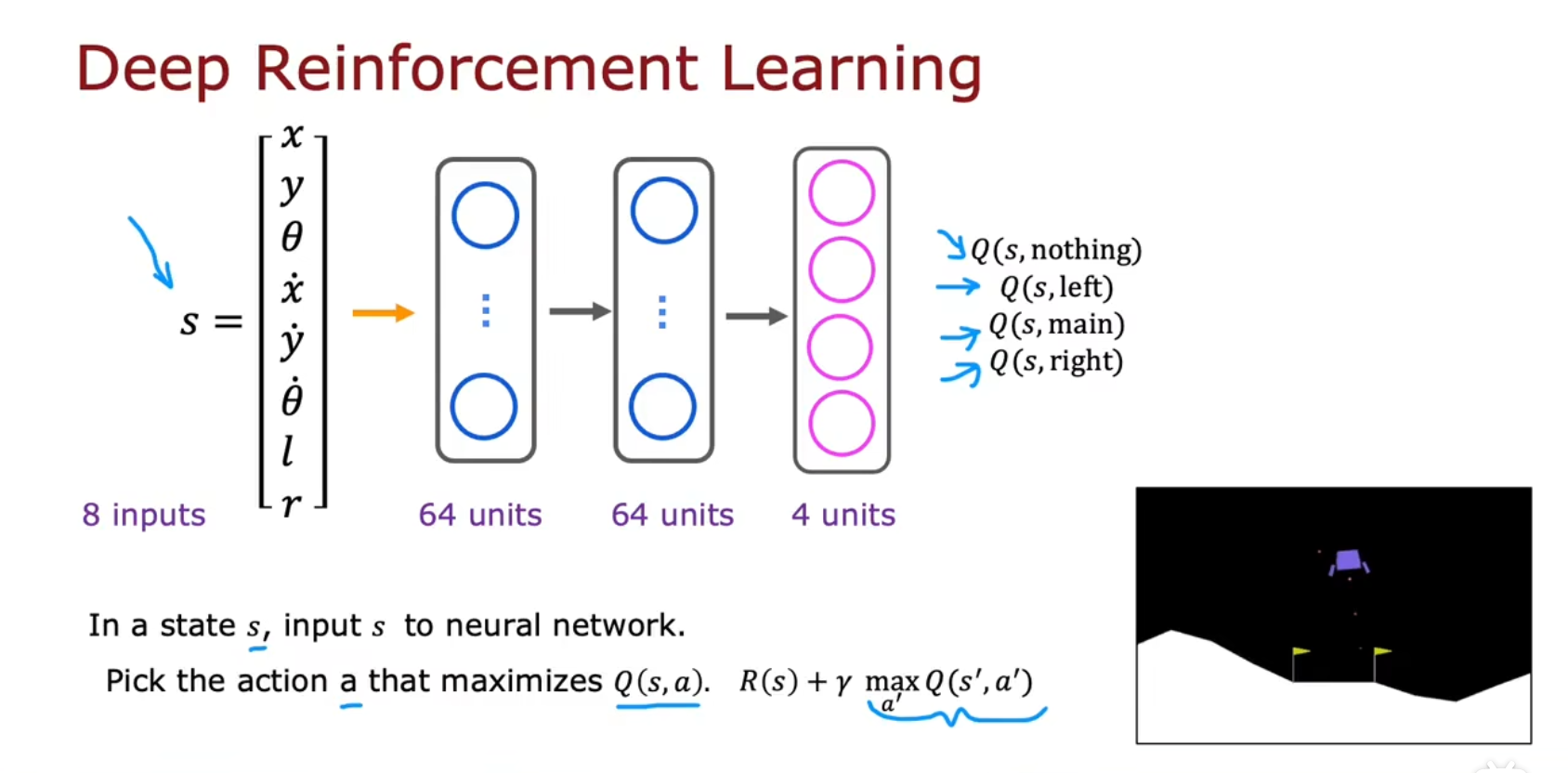
算法改进
改进的神经网络架构
每个状态要推理四次,有四个输出单元
ε贪婪策略(Epsilon-greedy policy)
步骤
将神经网络随机初始化为Q(s,a)的猜测
重复 {
在月球着陆器上采取行动。获得(s,a,R(s),s′)
存储10,000个最近(s,a,R(s),s′)元组
_
训练模型:
使用x=(s,a)和y=R(s)+γmaxa′(s′,a′),创建由10,000个示例组成的训练集
训练Qnew以Qnew(s,a)≈y。fw,b(x)≈y
设置Q=Qnew
} 直到收敛
在状态s时,有两个选项:
选项一
采取使Q(s,a)最大化的行动a
选项二(ε贪婪策略,Epsilon-greedy policy)
95%采取使Q(s,a)最大化的行动a(exploitation)
05%采取随机行动a
其中该例子中ε=0.05,或者说95%贪婪
一个技巧是,开始的时候ε设置较高,然后逐渐减少该值。比如从1.0开始,逐渐减少到0.01
小批量(Mini batch,可选)
除了强化学习,也适用于监督学习
比如如果有一亿多个数据时,梯度下降会很慢,每一次下降都要计算一亿多个数据
小批量梯度下降的思想是,比如这次下降选择1000个子集,下一次下降再选择另外1000个子集,节约时间

软更新(Soft update,可选)
除了强化学习,也适用于监督学习
令Q:=Qnew,由于Q(s,a)=Q(x)=fW,B(x)=y
即令
- W:=Wnew
- B:=Bnew
而**软更新(Soft update)**则是,令
- W:=0.01Wnew+0.99W
- B:=0.01Bnew+0.99B
软更新的作用:能让强化学习算法 更可靠地收敛,不容易振荡或转向或产生其他不良特性









