跳至主要內容

马尔可夫链算新抽卡概率

LincZero大约 3 分钟

马尔可夫链算新抽卡概率

原流程

流程

50%歪，50不歪。若歪则下一次必定不歪

期望概率

方式一：状态转移方程组

1.状态转移方程 π=[π(A)π(B)]×[toAtoBfromA0.50.5fromB1.00.0]=[π(A)π(B)] 2.展开得到方程组 {0.5π(A)+1.0π(B)=π(A)0.5π(A)+0π(B)=π(B)π(A)+π(B)=1 3.解方程组 {π(A)=23≈66.667%π(B)=13≈33.333% 1. 状态转移方程\\~\\ \pi = \begin{bmatrix} \pi(A) &\pi(B) \end{bmatrix} \times \begin{bmatrix} &toA &toB\\ fromA &0.5 &0.5\\ fromB &1.0 &0.0 \end{bmatrix} = \begin{bmatrix} \pi(A) &\pi(B) \end{bmatrix} \\~\\ 2. 展开得到方程组\\~\\ \begin{cases} 0.5\pi(A)+1.0\pi(B) &= \pi(A)\\ 0.5\pi(A)+0\pi(B) &= \pi(B)\\ \pi(A)+\pi(B) &= 1 \end{cases} \\~\\ 3. 解方程组\\~\\ \begin{cases} \pi(A) &= \frac 23 \approx 66.667\% \\ \pi(B) &= \frac 13 \approx 33.333\% \end{cases}

方式二：马尔可夫链，并使用概率转移矩阵来进行计算（更适合计算机运算的方法）

概率转移矩阵P=[toAtoBfromA0.50.5fromB1.00.0] 一次转移=[10]⋅P=[0.50.5] 二次转移=[10]⋅P2=[10]⋅[0.750.250.50.5]=[0.750.25] 很多次转移=[10]⋅PN=[0.666670.33333] \begin{align} 概率转移矩阵P&= \begin{bmatrix} &toA &toB\\ fromA &0.5 &0.5\\ fromB &1.0 &0.0 \end{bmatrix} \\~\\ 一次转移&= \begin{bmatrix} 1 &0\\ \end{bmatrix} \cdot P= \begin{bmatrix} 0.5 &0.5\\ \end{bmatrix} \\~\\ 二次转移&= \begin{bmatrix} 1 &0\\ \end{bmatrix} \cdot P^2 = \begin{bmatrix} 1 &0\\ \end{bmatrix} \cdot \begin{bmatrix} 0.75 &0.25\\ 0.5 &0.5 \end{bmatrix} = \begin{bmatrix} 0.75 &0.25\\ \end{bmatrix} \\~\\ 很多次转移&= \begin{bmatrix} 1 &0\\ \end{bmatrix} \cdot P^N = \begin{bmatrix} 0.66667 &0.33333\\ \end{bmatrix} \end{align}

新概率

流程

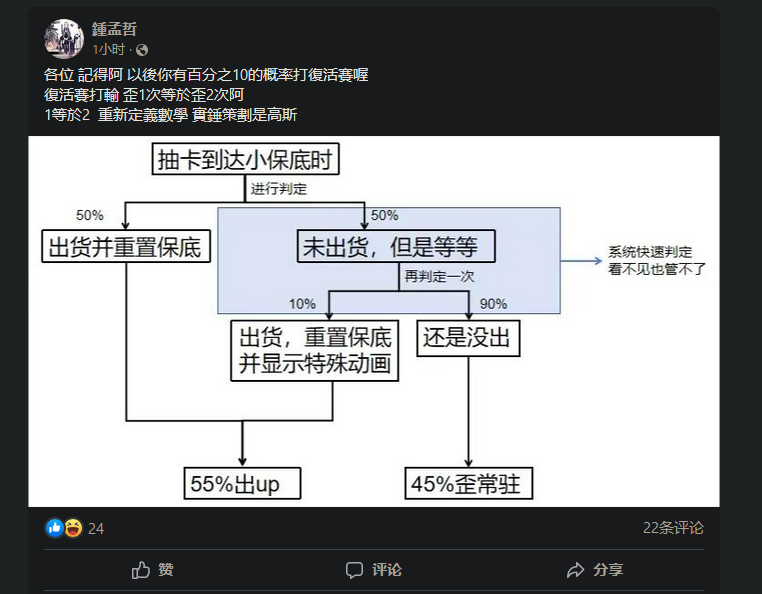
完整的程序机制：

可以将上图简化，完全等效为：

我们也可以，抛弃保底机制，转化为纯期望模型：

期望概率

状态转移方程组

1.状态转移方程 π=[π(A)π(B)]×[toAtoBfromA0.550.45fromB1.00.0]=[π(A)π(B)] 2.展开得到方程组 {0.55π(A)+1.0π(B)=π(A)0.45π(A)+0π(B)=π(B)π(A)+π(B)=1 3.解方程组 {π(A)=100145=2029≈68.966%π(B)=45145=929≈31.034% 1. 状态转移方程\\~\\ \pi = \begin{bmatrix} \pi(A) &\pi(B) \end{bmatrix} \times \begin{bmatrix} &toA &toB\\ fromA &0.55 &0.45\\ fromB &1.0 &0.0 \end{bmatrix} = \begin{bmatrix} \pi(A) &\pi(B) \end{bmatrix} \\~\\ 2. 展开得到方程组\\~\\ \begin{cases} 0.55\pi(A)+1.0\pi(B) &= \pi(A)\\ 0.45\pi(A)+0\pi(B) &= \pi(B)\\ \pi(A)+\pi(B) &= 1 \end{cases} \\~\\ 3. 解方程组\\~\\ \begin{cases} \pi(A) &= \frac {100}{145} = \frac {20}{29} \approx 68.966\%\\ \pi(B) &= \frac {45}{145} = \frac {9}{29} \approx 31.034\% \end{cases}

最终结论

  1. 当我们看到：歪了以后有 10%10\% 概率变歪为不歪，会觉得 10%10\% 好多啊

  2. 当我们看到：非保底出up的概率从 50%50\% 提高到了 55%55\%，会觉得提高了 5%5\%，还行吧，聊胜于无

  3. 当我们看到：新概率相较于旧概率，平均的up出金率提高了 “惊人的” 2.299%2.299\%。就感觉少了。 （即每一百个金/每66.67个Up角色，会多2.299个Up角色）

  4. 平均多少抽多一个金？

    在没有修改概率的时间线中，不欧不非的你会在 5.0 版本后抽了43个金。其中28.667个Up角色了，14.333个非Up角色。 而在新时间线中，这个机制在期望上能让不欧不非的你会抽到29.655个金，相较于另一个时间线的自己刚好少一个常驻金，而多一个Up金。

所以说，为什么在前瞻中要把概率提高说得那么绕，而不是简单地跟你说概率提高了多少多少，就是让你觉得概率提高了好多