《高等数学》
目录
[toc]
导数与微分
导数概念
导数
定义
原定义
设函数y=f(x)在点x0的某个领域内有定义,当自变量x在x0处取得增量Δx(点x0+Δx仍在该邻域内)时,因变量取得增量Δy=f(x0+Δx)−f(x0);如果ΔxΔy当Δx→0时的极限存在,那么称函数y=f(x)在点x0处可导,并称这个极限为函数y=f(x)在点x0处的导数记为f′(x),即:
f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)
记作:f′(x0)、y′∣x=x0、dxdy∣x=x0、dxdf(x)∣x=x0
意义
概念
- 导函数
- 记作:f′(x)、y′、dxdy、dxdf(x)
- 单侧导数
可导性、连续性、极限
- f(x)在x处左右极限存在(且不为无穷)且相等⇔f(x)在x处可导⇒f(x)在x处连续⇔f(x)在x处左右极限存在
- 连续不一定可导的反例:y=3x、折线图等
斜率补充(个人补充)
(切函数、倒函数(倒数函数)、负函数我也不知道是不是这么叫,名字拟定)
| 斜率 | 斜率表示 | 函数图像 | 函数式子 |
|---|
| 原函数切线斜率 | y′或dxdy | 原图像 | y=f(x) 或 y=f(x)+b |
| 原函数法线斜率 | −y′1 | 无(对应于点,法线垂直于各点切线) | (y−y0)=k(x−x0) |
| 切函数切线斜率 | −y′1 | (略) | (略) |
| 倒函数切线斜率 | −f(x)2f′(x) | 坐标轴分区并极限缩放后,原图像沿着线y=1对称 | y=f(x)1 |
| 负函数切线斜率 | −y′ | 原图像沿x轴对称 | y=−f(x) |
| 反函数切线斜率 | y′1或dydx或dxdy1 | 原图像连坐标轴沿直线y=x对称 | x=f(y)或y=f−1(x) |
函数的求导法则
求导法则(繁琐版)
求导法则(繁琐版)(可跳过,后面有精简版)
求导法则【定理1】和差积商:如果函数u=u(x)及v=v(x)都在点x具有导数,那么它们的和差积商(除分母为0的点外)都在点x具有导数,且(1)[u(x)±v(x)]′=u′(x)±v′(x)(2)[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x)(3)[v(x)u(x)]′=v2(x)u′(x)v(x)−u(x)v′(x)(v(x)=0)
求导法则【定理2】反函数:如果函数x=f(y)在区间Iy内单调、可导且f′(y)=0,那么它的反函数y=f−1(x)在区间Ix={x∣x=f(y),y∈Iy}内也可导,且[f−1(x)]′=f′(y)1 或 dxdy=dydx1
求导法则【定理3】复合函数:如果u=g(x)在点x可导,而y=f(u)在点u=g(x)可导.那么复合函数y=f[g(x)]在点x可导,且其导数为f′(x)=dxdy=f′(u)⋅g′(x)或dxdy=dudy⋅dxdu
基本求导法则与导数公式(要背)
导数公式
导数公式【1】常量 / 幂函数类
- (C)′=0
- (xμ)′=μxμ−1
导数公式【2】三角与反三角类
- \begin{align} (\sin x)'&=\cos x& (\cos x)'&={\color{red}-}\sin x\\ (\tan x)'&=\sec^2 x& (\cot x)'&={\color{red}-}\csc^2 x\\ (\sec x)'&=\sec x\tan x& (\csc x)'&={\color{red}-}\csc x\cot x\\ (\arcsin x)'&=\frac1{\sqrt{1-x^2}}& (\arccos x)'&={\color{red}-}\frac1{\sqrt{1-x^2}}\\ (\arctan x)'&=\frac1{1+x^2}& (arccot~x)'&={\color{red}-}\frac1{1+x^2}'\\ (arcsec~x)'&=\frac{1}{|x|\sqrt{x^2-1}}&(arccsc~x)'&={\color{red}-}\frac{1}{|x|\sqrt{x^2-1}} \end{align}
导数公式【3】对数指数类
- \begin{align} &(1)(a^x)'=a^x\ln a(a>0,a\neq1) &&(2)(e^x)'=e^x\\ &(3)(log_ax)'=\frac1{x\ln a}(a>0,a\neq1) &&(4)(\ln x)'=\frac1x \end{align}
求导法则(精简版)
- 求导法则【定理1简写】和差积商:\begin{align} &(1)(u\pm v)'=u'\pm v' &&(2)(Cu)'=Cu'(C是常数)\\ &(3)(uv)'=u'v+uv' &&(4)(\frac{u}{v})'=\frac{u'v-uv'}{v^2}(v\neq0) \end{align}
- 求导法则【定理2】反函数:[f−1(x)]′=f′(y)1 或 dxdy=dydx1
- 求导法则【定理3】复合函数:f′(x)=f′(u)⋅g′(x)或dxdy=dudy⋅dxdu
三角函数补充(自增)
高中不用csc、sec、cot,而大学不学直接就用。这里补充一下关系和性质等
| 求导式 | 值 | 英文名 | 中文口诀 | 等价值 |
|---|
| (sinx)′ | +cosx | sine | 正弦−余弦 | —— |
| (cosx)′ | −sinx | cosine | $${\color{red}余}弦 - 正弦{\color{red}(负)}$$ | —— |
| (tanx)′ | +sec2x | tangent(旧版tg) | $${\color{blue}正}切 - 正割割$$ | —— |
| (cotx)′ | −csc2x | cotangent | $${\color{red}余}切 - 余割割{\color{red}(负)}$$ | (tanx1)′倒数关系 |
| (secx)′ | +secxtanx | secant | $${\color{blue}正}割 - 正割切$$ | (cosx1)′倒数关系 |
| (cscx)′ | −cscxcotx | cosecant | $${\color{red}余}割 - 余割切{\color{red}(负)}$$ | (sinx1)′倒数关系 |
| (arcsinx)′ | +1−x21 | —— | $$反{\color{blue}正}弦$$ | 反函数关系 |
| (arccosx)′ | −1−x21 | —— | $$反{\color{red}余}弦{\color{red}(负)}$$ | 反函数关系 |
| (arctanx)′ | +1+x21 | —— | $$反{\color{blue}正}切$$ | 反函数关系 |
| (arccot x)′ | −1+x21 | —— | $$反{\color{red}余}切{\color{red}(负)}$$ | 反函数关系 |
| (arcsec x)′ | ${\color{blue}+}\frac{1}{ | x | \sqrt{x^2-1}}$ | —— |
| (arccsc x)′ | ${\color{red}-}\frac{1}{ | x | \sqrt{x^2-1}}$ | —— |
三角函数导数记法(六边形记法)
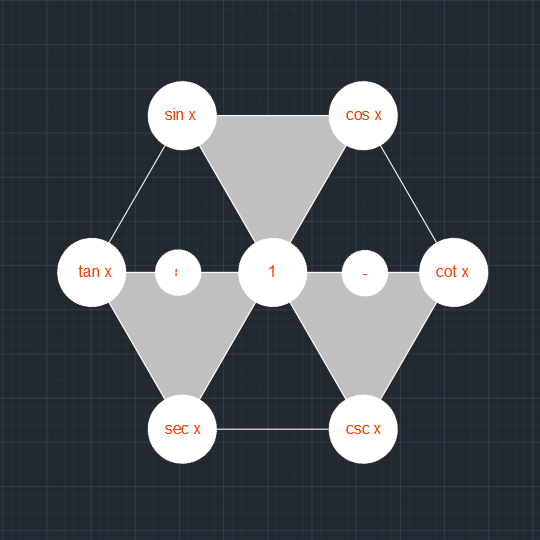
题型(自增)
求导数题
通用型化简技巧
- 减元法(部分):通用:b(x+b)c−xc=xc−1⋅xb(1+xb)c−1
高阶导数
n阶导数
- 定义
- n阶导数定义:一阶导数的导数叫做二阶导数,以此类推,(n−1)阶导数的导数叫做n阶导数
- n阶可导定义:函数y=f(x)具有n阶导数,也常说成函数f(x)为n阶可导
- 高阶导数定义:二阶及二阶以上的导数统称高阶导数
题型(自增)
求n阶导数
- 莱布尼兹(Leibniz)公式(第二条才是)
- 幂函数xμ的n阶导数:(xμ)(n)=μ(μ−1)(μ−2)⋯(μ−n−1)xμ−n特别的,当μ=n时,(xn)(n)=n!
- u(x)⋅v(x)的n阶导数:(uv)(n)=∑k=0nCnku(n−k)v(k)=k!n(n−1)⋯(n−k−1)u(n−k)v(k)⋯uv(n)(用数学归纳法列出式子,再用二项式定理展开(u+v)n化简定理)
非显函数求导(隐函数及由参数方程所确定的函数的导数、相关变化率)
隐函数
定义
- 显函数:等号左端是因变量的符号,而右端是含有自变量的式子
- 隐函数:不符合显函数规律的,用方程表示的函数
- 隐函数的显化:把一个隐函数化成显函数
隐函数求导方法
把方程两边分别对x求导数
注意:y看作x的复合函数,通常f(y)′的结果为g(y,y′)y′=y′,x′=1,0′=0
其实和先函数没有本质区别,都是一样的
把y看成:v(x)=y←x,其中v′=y′把x看成:u(x)=x,其中u′=1(xy)′=(uv)′=uv′+u′v=xy′+y(lny)′=(lnv)′=v1v′=y1y′
【技巧】对数求导法
- 方法:
先在y=f(x)两边取对数,然后再求出y的导数(其实感觉直接对数指数更快) - 举例:y=xsinx⇒lny=sinx⋅lnx⇒y1y′=cosx⋅lnx+xsinx⇒y′=y(cosx⋅lnx+xsinx)⇒xsinx(cosx⋅lnx+xsinx)
由参数方程所确定的函数的导数
相关变化率(没用)
- 定义
- 设x=x(t)及y=y(t)都是可导函数,而变量x与y间存在某种关系,从而变化率dtdy与dtdy间也存在一定关系这两种相互依赖的变化率称为相关变化率
题型(自增)
- 隐函数求导
- 显函数使用隐函数技巧求导
- 易错:f(x)g(x)不是复合函数!!!
- xx 或 f(x)g(x),指对法可得例1:y′=(exlnx)′=xx(lnx+1)例2:(xsinx)′=(esinxlnx)′=xsinx(cosxlnx+xsinx)易错:这不是复合函数,如例2拆解成:y←u=xa,u←x=sinx时, y←u的变量不是u而是x,而且a不是u
函数的微分
微分的定义与几何意义
基本初等函数的微分公式与微分运算法则
微分公式(同导数公式)
微分表达式:dy=f′(x)dx
- 导数公式:f′(x)=g(x)
- 微分公式:df(x)=g(x)dx
微分法则(同导数法则)
- 微分法则【和差积商】:导数法则的基础上,u′→du,v′→dv即可(等式两边都是导数式的前提下,相当于两边同乘以dx)
- 微分法则【复合函数】:∵f′(x)=f′(u)⋅g′(x)∴dy=f′(u)du(微分形式不变性)
微分在近似计算中的应用
函数的近似计算
- 工程常用近似公式(都是前面提到过的等价无穷小)
- (1+x)α∼1+αx (α∈R)
- sinx∼x (x用弧度制)
- tanx∼x (x用弧度制)
- ex∼1+x
- ln(1+x)∼x
误差估计
- 概念
- 间接测量误差
- 绝对误差:∣A−a∣
- 相对误差:∣a∣∣A−a∣
- 绝对误差限(简称绝对误差):∣A−a∣≤δA=测量A的绝对误差限
- 相对误差限(简称相对误差):∣a∣δA=测量A的相对误差限
总结(自增)
总结(自增)
定理总结(课本)
基本求导法则与导数公式(要背)
导数公式
导数公式【1】常量 / 幂函数类
- (C)′=0
- (xμ)′=μxμ−1
导数公式【2】三角与反三角类
- \begin{align} (\sin x)'&=\cos x& (\cos x)'&={\color{red}-}\sin x\\ (\tan x)'&=\sec^2 x& (\cot x)'&={\color{red}-}\csc^2 x\\ (\sec x)'&=\sec x\tan x& (\csc x)'&={\color{red}-}\csc x\cot x\\ (\arcsin x)'&=\frac1{\sqrt{1-x^2}}& (\arccos x)'&={\color{red}-}\frac1{\sqrt{1-x^2}}\\ (\arctan x)'&=\frac1{1+x^2}& (arccot~x)'&={\color{red}-}\frac1{1+x^2}'\\ (arcsec~x)'&=\frac{1}{|x|\sqrt{x^2-1}}&(arccsc~x)'&={\color{red}-}\frac{1}{|x|\sqrt{x^2-1}} \end{align}
导数公式【3】对数指数类
- \begin{align} &(1)(a^x)'=a^x\ln a(a>0,a\neq1) &&(2)(e^x)'=e^x\\ &(3)(log_ax)'=\frac1{x\ln a}(a>0,a\neq1) &&(4)(\ln x)'=\frac1x \end{align}
求导法则(精简版)
- 求导法则【定理1简写】和差积商:\begin{align} &(1)(u\pm v)'=u'\pm v' &&(2)(Cu)'=Cu'(C是常数)\\ &(3)(uv)'=u'v+uv' &&(4)(\frac{u}{v})'=\frac{u'v-uv'}{v^2}(v\neq0) \end{align}
- 求导法则【定理2】反函数:[f−1(x)]′=f′(y)1 或 dxdy=dydx1
- 求导法则【定理3】复合函数:f′(x)=f′(u)⋅g′(x)或dxdy=dudy⋅dxdu
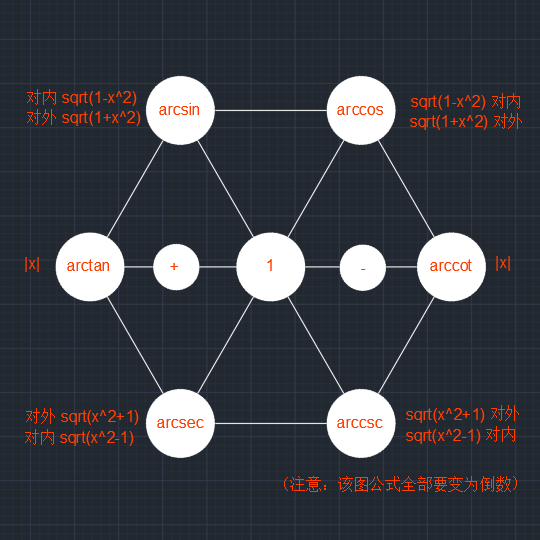
三角函数导数记法(六边形记法)


非显函数求导
隐函数求导方法
- 把方程两边分别对x求导数
- 注意:y看作x的复合函数,通常f(y)′的结果为g(y,y′)y′=y′,x′=1,0′=0
参数方程求导方法
对比总结(自增)
可微、可导、连续、严格连续
两者的定义区别(仅比较定义表述)
一致连续性定义
定义表述:(“ε−δ”语言)
f(x)一致连续⇔∀ε>0,∃δ>0,当∣x1−x2∣<δ时,有∣f(x1)−f(x2)∣<ε
连续性定义
定义表述:(“ε−δ”语言)
f(x)在点x0连续⇔∀ε>0,∃δ>0,当∣x−x0∣<δ时,有∣f(x)−f(x0)∣<ε
连续性和一致连续性的区别
- 在闭区间没有区别:根据定理4(一致连续性定理),闭区间连续则为一致连续
- 在开区间时有区别:(图像区别比较好理解)
- 范围不同:一致连续是整体性质,连续是点的局部性质,从定义可见得
- 包含关系:一致连续⊂连续⇐可导
- 图像区别:一致连续的函数图像不存在上升或下降坡度无限变陡的情况,连续却可以
- 反例(函数连续但不一致连续):如:y=x1、y=x2(x∈[0,∞])等等
导数、微分
多元才有区别
可导可微
结论口诀
- 可导⇒连续⇒可导
- 一致连续⊂连续,闭区间内:一致连续=连续



