吴恩达机器学习

目录

单变量线性回归模型（Linear Regression）

单变量线性回归模型

线性回归模型

回想一下在回归问题中，我们使用输入变量，并试图将输出拟合到连续的预期结果函数中。

具有一个变量的线性回归也称为“单变量线性回归”。

当要根据单个输入值x预测单个输出值y时，使用单变量线性回归。我们在这里使用监督学习，意味着我们已经对输入/输出因果关系有一个了解。

① 假设函数

我们的假设函数具有以下一般形式：（单变量线性回归）

$$\hat{y}=h_{\theta}(x)=\theta_{0}+\theta_{1}x$$

输入x，称为 输入变量 ( input variable)，也称为 特征 (feature) 或 输入特征 (input feature)
输出y，称为 输出变量 (output variable)，也称为 目标变量 (target variable)

请注意，这是一条直线方程形式。我们通过$\theta_{0}$和$\theta_{1}$赋予的$h_{\theta}(x)$的值，得到我们的预测输出$\hat{y}$。换句话说，我们正在尝试创建一个名为$h_{\theta}(x)$的函数，将我们的输入数据(x)映射到我们的输出数据(y)。

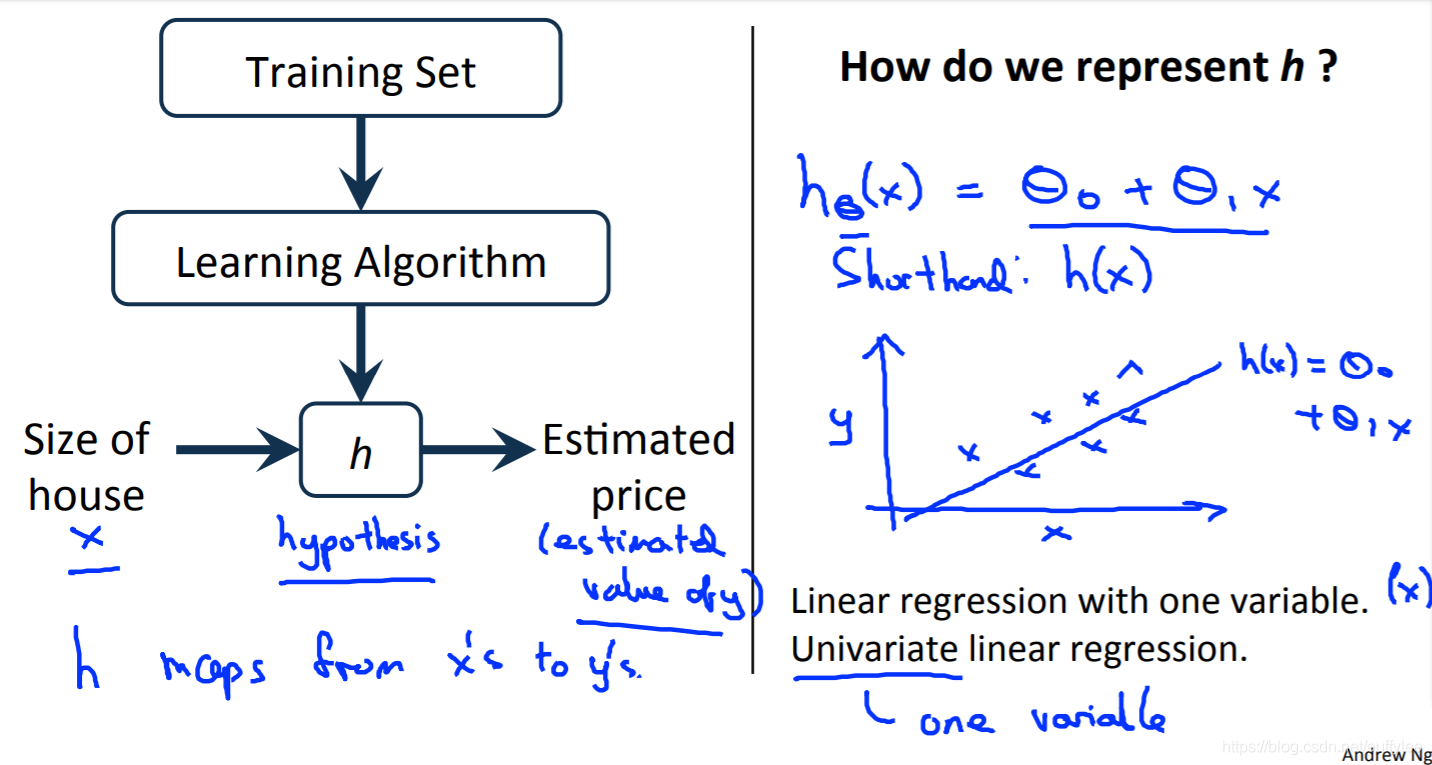
例：

假设我们具有以下训练数据集：

输入x	输出y
0	4
1	7
2	7
3	8

现在我们可以随意猜测一下$h_{\theta}$函数：$\theta_0=2$和$θ\theta_1=2$。假设函数变为$h_{\theta}(x)=2+2 x$。

因此，若假设函数的输入x为1，y则为4。注意，我们尝试各种$\theta_{0}$和$\theta_{1}$的值，试图通过映射在xy平面上的数据点找到最佳“拟合”或最具代表性的“直线”的值

② 代价函数

Cost Function：代价函数、也能翻译成成本函数

代价函数公式

其实几乎就是高中学的最小二乘法，略有不同（比如要除以2m）

将每项预测值和实际值的差的平方累积起来，这种代价函数叫 “平方误差成本函数”（squared error cost function）

我们可以使用代价函数来衡量假设函数的准确性。把假设函数的所有结果取平均值（实际上是平均值的简化版），将输入x得到$h_{\theta}(x)$的与实际输出y进行比较

$$J\left(\theta_{0}, \theta_{1}\right) = \frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2} = \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2} \\~\\-------------------\\ \begin{align} 线性模型函数&：y=wx+b\\~\\ 预测值&：\hat y_i=f_{w,b}(x_i)=wx_i+b\\ 代价函数&：J\left(w, b\right)= \frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}= \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2} \end{align}$$

现在，我们可以根据已知的正确输出y具体衡量我们的预测函数$h_{\theta}(x)$的准确性，以便预测不在现有数据集中的输入x的输出结果

理解代价函数

其他说明

$h_{\theta}\left(x_{i}\right)-y_{i}$是预测值与实际值之差

$\bar{x}$是 $(h_{\theta}\left(x_{i}\right)-y_{i})^2$的均值 ，$\bar{x}$也被称为 “平方误差函数” 或 “均方误差”

当完全符合时，代价函数值为0
我们的目标是取得最优拟合线，即使散点与该线的平均垂直距离最小的线。在理想的最优情况下，该线应穿过训练数据集的所有点，即$J\left(\theta_{0}, \theta_{1}\right)$为0

为什么要除以2m？（$\frac{1}{2 m}$）

1. 除以m是因为我们将计算平均平方误差而不是总平方误差，平均平方误差会不随着训练数据增多而增多
2. 除以2是为了后面方便计算梯度下降，因为平方函数求导后的导数项将抵消$\frac{1}{2}$

$$\begin{align} model~~~~~~~~模型：&~f_{w,b}(x)=wx+b\\ parameters~~~~~~~~参数：&~w,b\\ cost~function~~代价函数：&~J\left(w, b\right)= \frac{1}{2 m} \sum_{i=1}^{m}\left(f_{w,b}\left(x_{i}\right)-y_{i}\right)^{2}\\ objective/goal~~~~~~~~~目的：&~\mathrm{minimize}_{w,b}J(w,b)\\ ---------&---------\\ (过原点时)~ simplified~~~~~~~~~化简：&~f_w(x)=wx，b\neq0\\ &J(w)=\frac 1{2m}\sum^m_{i=1}(f_w(x^i)-y^i)^2\\ &\mathrm{minimize}_w J(w) \end{align}$$

可视化代价函数

可视化 - 线性回归模型代价函数的函数图

这种图也叫 凸面函数（convex function）
（Q：为什么不叫凹函数？A：标准的优化问题是求最小值，定义向下凸为凸函数，上凸为凹函数）

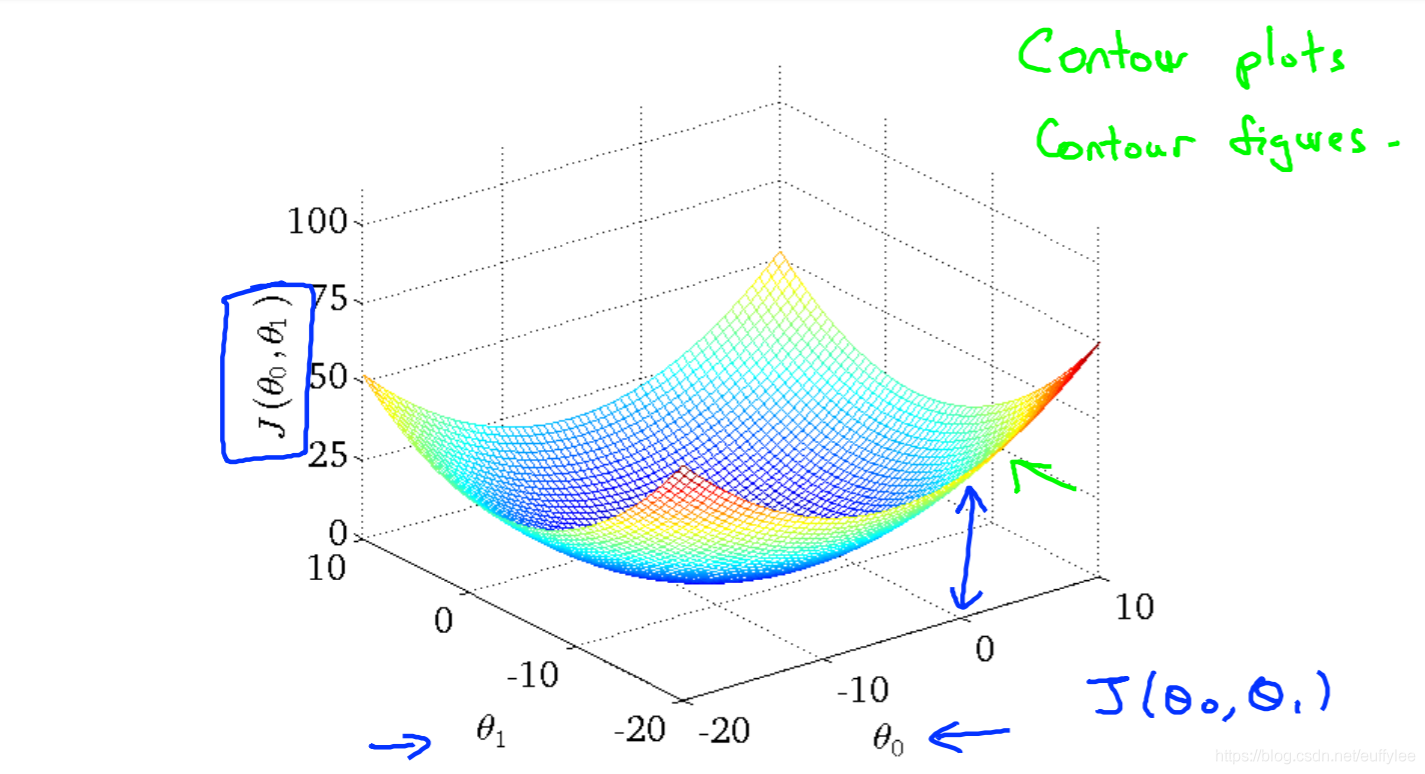
从可视化角度看，训练数据集散布在$x-y$平面上。我们尝试使直线（由$h_{\theta}(x)$定义）穿过这些分散的数据集。

③ 梯度下降

概念

概念

对于单参数线性回归模型来说，三维函数图为碗状，其代价函数最小值时的w和b也比较容易找到，甚至可以通过简化最小二乘法直接算得。
但对于更复杂的模型来说，想要找到最小值，需要一种高效的算法来自动查找w和b —— 梯度下降算法

梯度下降在机器学习中极为常见，不仅能用于回归模型，还能用于最先进的神经网络模型（深度学习模型）

可视化

想象一下，我们根据假设参数$\theta_{0}$和$\theta_{1}$的范围绘制假设函数图像（实际上，我们将代价函数绘制为参数估计值的函数）。
这可能会造成混淆；我们正在向更高的抽象水平发展。我们不是在绘制x和y本身，而是绘制假设函数的参数范围以及选择特定参数集所产生的代价。
我们把$\theta_{0}$对应x轴上，$\theta_{1}$对应y轴，代价函数对应垂直的z轴。图上的点是使用假设函数和特定的$\theta$参数的代价函数的所得结果。

当代价函数位于图中凹坑的最底部时，即当其值最小时，梯度下降就成功了

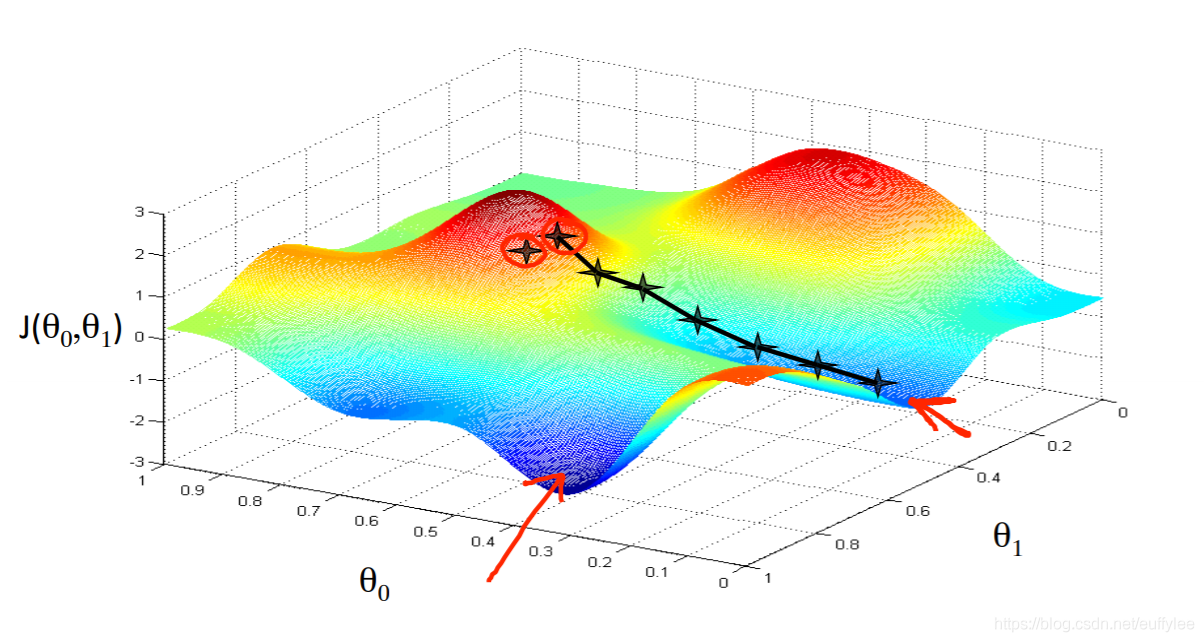
根据起始点的不同，得到的最小值可能也不同

情况1：

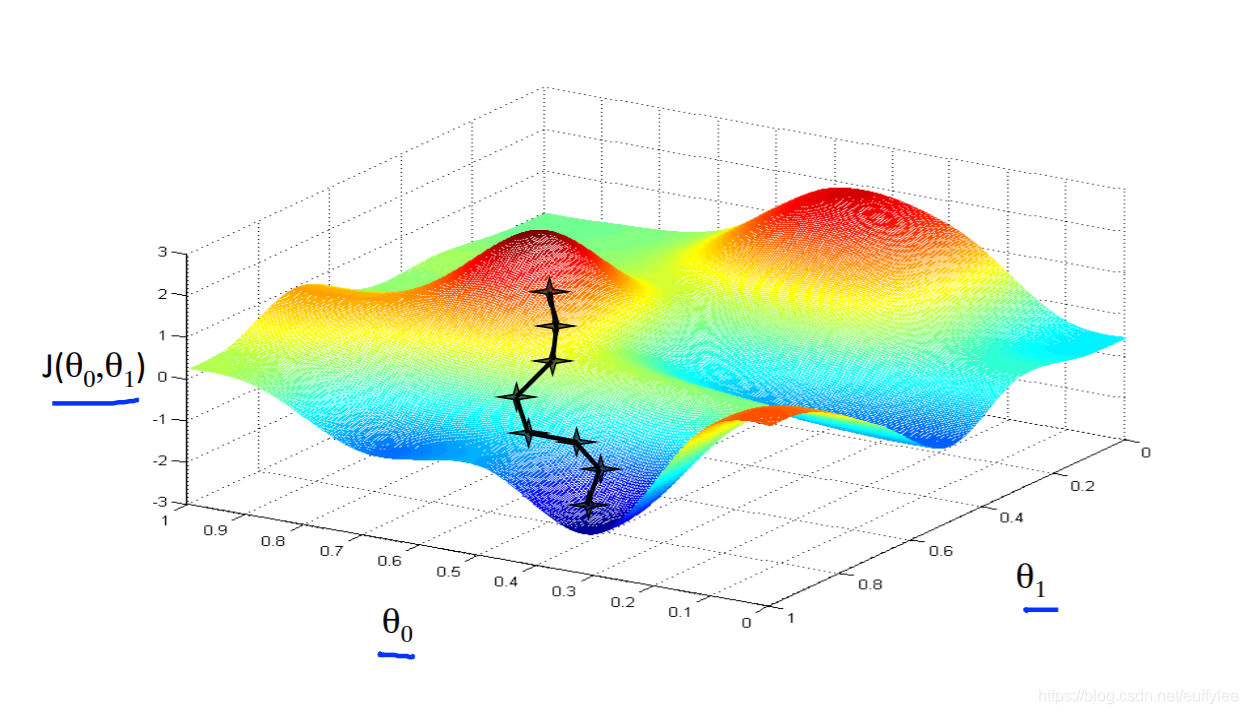
情况2：

梯度下降的实现

数学原理

基本原理

① 目标是得到$\min_{w,b}J(w,b)$

② 首先要设置w,b初始值，通常设置为$w=0,~b=0$

③ 然后改变w,b去减少$J(w,b)$

④ 直到J达到局部最小值 (极点)

——————————————————————

具体方案

方法是采用代价函数的导数（函数的切线）。切线的斜率是该点的导数，它将为我们提供一个方向。
我们沿下降最陡的方向降低代价函数，每一步的大小由参数α（即学习效率）决定

——————————————————————

即重复下式 直到收敛

$$~~~~~~~~\theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)\\ 或~w:=w-\alpha\frac\partial{\partial w}J(w,b)\\$$

其中

• $(:=)$表示赋值的意思

• $\partial $ 表示求偏导符号，可以读作round，

  • $\frac{\partial J(w,b)}{\partial w}$ 就是函数$J(w,b)$ 对$w$ 求偏导，在代码中我们会使用$dw$ 表示这个结果，

    $\frac{\partial J(w,b)}{\partial b}$ 就是函数$J(w,b)$对$b$ 求偏导，在代码中我们会使用$db$ 表示这个结果，

  • 小写字母$d$ 用在求导数（derivative），即函数只有一个参数，

    偏导数符号$\partial $ 用在求偏导（partial derivative），即函数含有两个以上的参数。

伪代码

注意的是对于多变量求偏导来说，对两边的求导是同时进行的

$$\begin{aligned} tmp\_w =& w-\alpha\frac\partial{\partial w}J(w,b)\\ tmp\_b =& b-\alpha\frac\partial{\partial b}J(w,b)\\ w=&tmp\_w\\ b=&tmp\_b\\ \end{aligned}\\~$$

学习率 $\alpha$（Learning Rate）

$\alpha$是对斜率的增幅，也叫学习率（learning rate），学习率左侧的部分是导数（derivative）
学习率值过小和过大会产生如下问题：

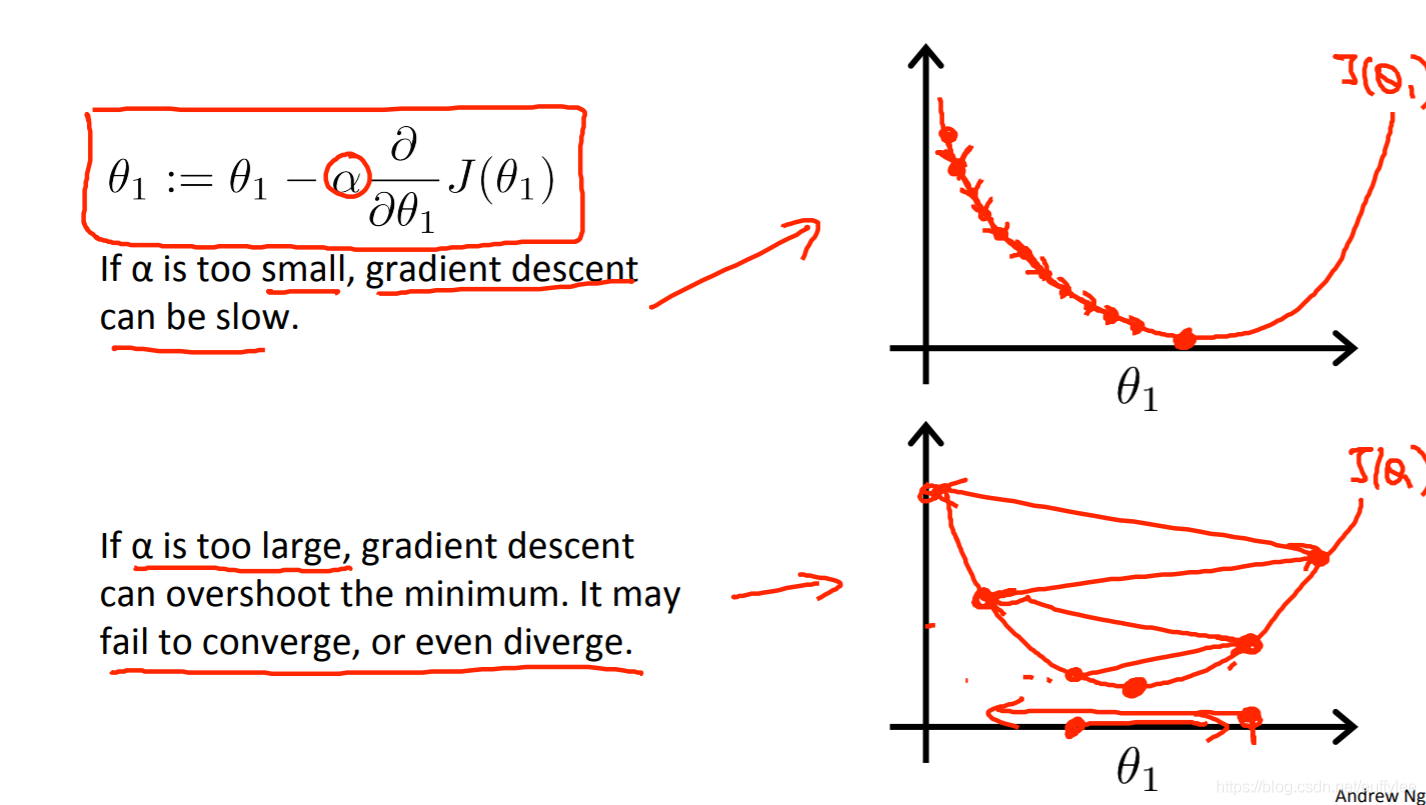
学习曲线

画一个$iterations~-~J(\vec w,b)$的图像，这也叫学习曲线（learning curve），单迭代次数足够多时，代价函数的值收敛
在梯度下降算法中，如果发现曲线未收敛但增大了，可能是学习率设置过大所导致的

判断梯度下降是否收敛

定义判断收敛：设置一个极小值$\epsilon$，值例如0.001。如果在一次迭代中，成本J的减少幅度小于这个设定值，那么可以声明收敛了

如何设置学习率

如果在学习曲线中，发现图像有明显的上下波动而不是单调递减的，则可能是学习率设置过大所导致的

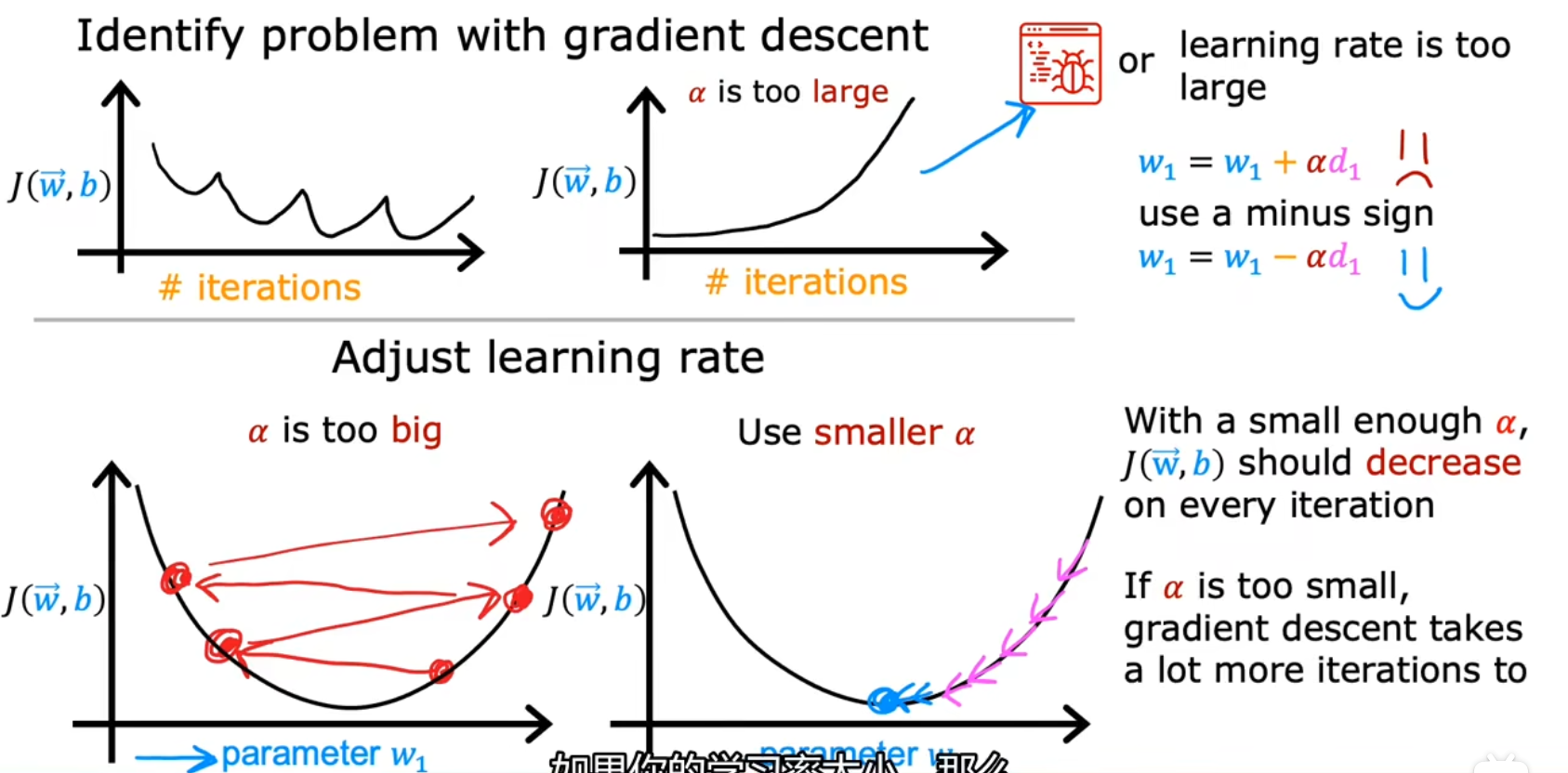
可以尝试多种学习率：…、0.001、0.01、0.1、1、…
然后看学习曲线，如果收敛速度太慢则学习率过小，如果学习曲线出现明显波动则学习率过大

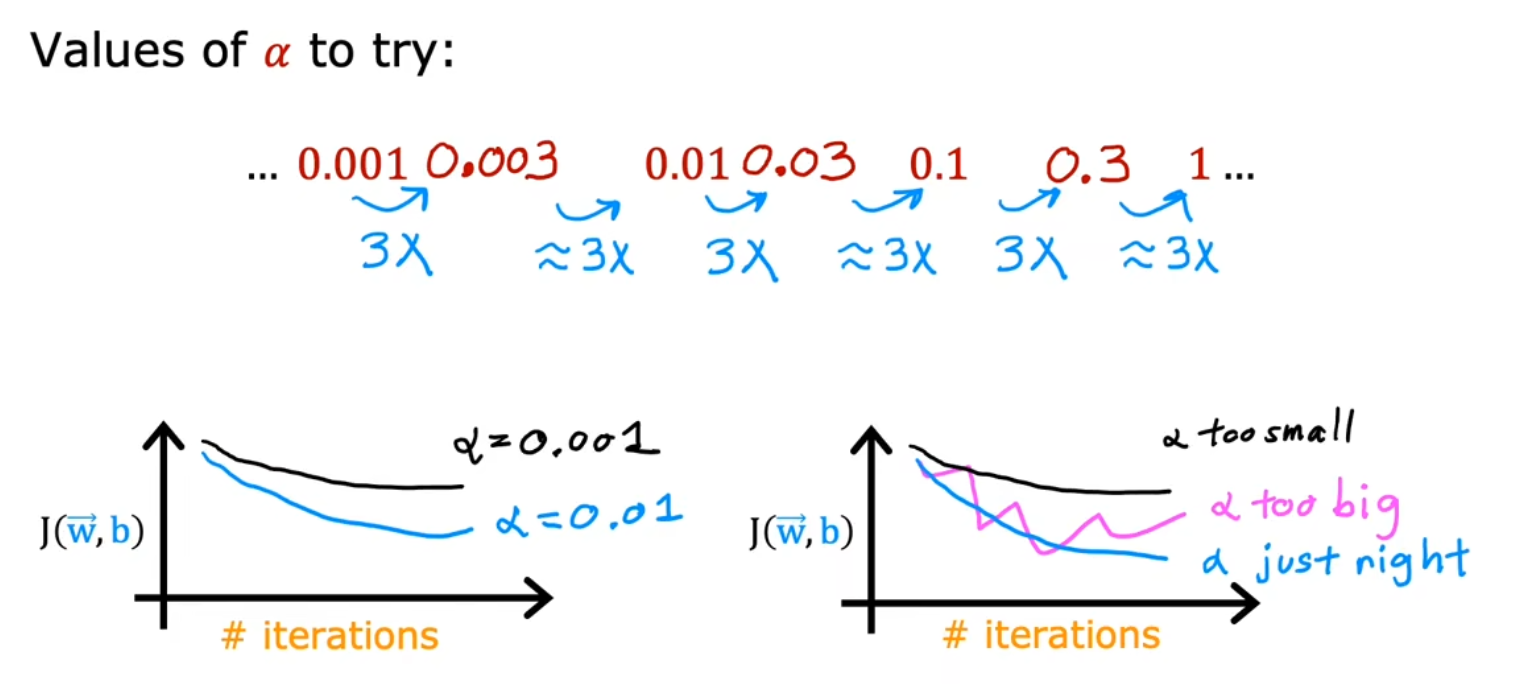
收敛速度

收敛速度越来越慢的原因 如下

导数$\frac{\partial}{\partial w}J(w,b)$越来越小，即斜率的绝对值越来越小，步进速度会越来越满

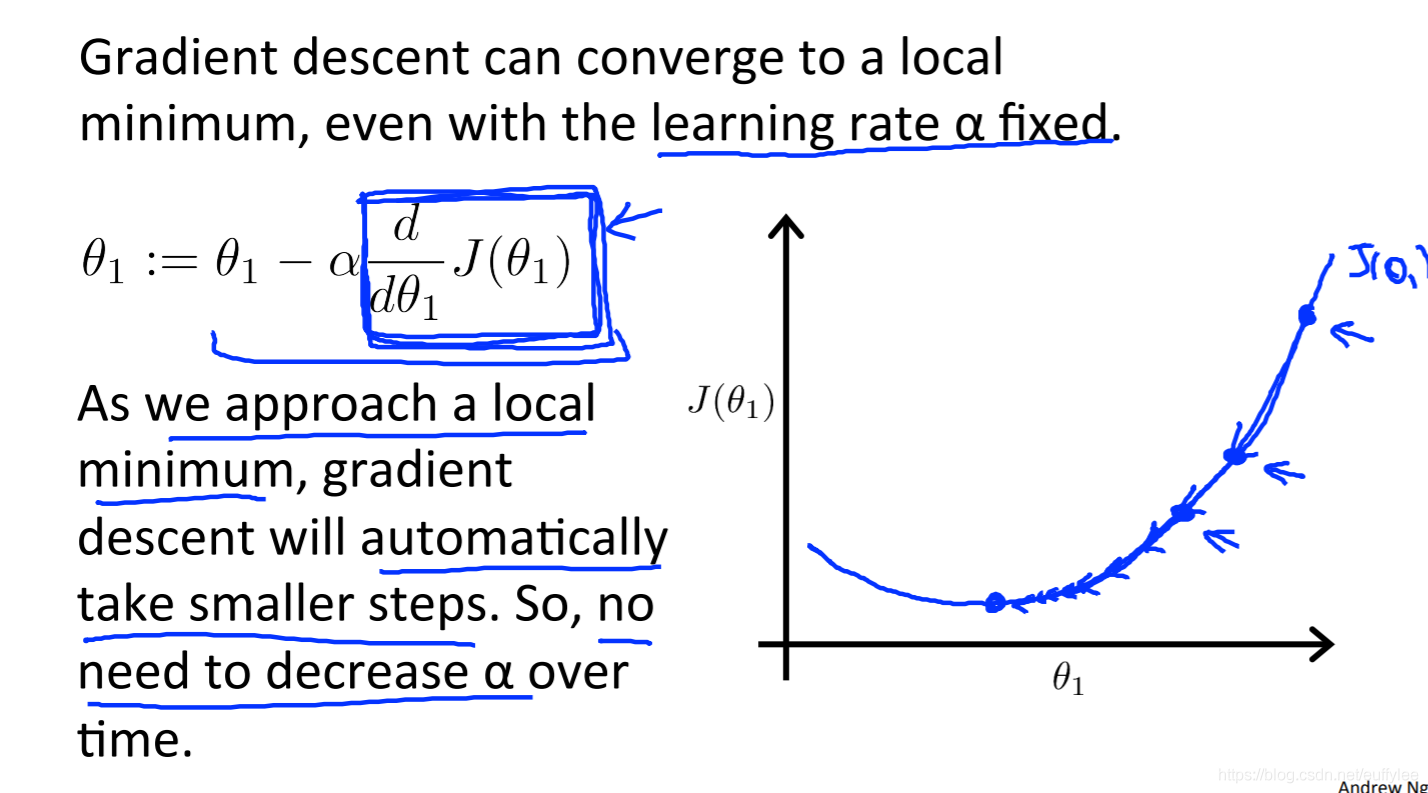
理想情况是完全到达最低点，倒数为0，此时$w:=w$，w的值稳定

线性回归的梯度下降

其他参考：Alexander Ihler:线性回归的梯度下降

当专门用于线性回归时，可以得出新形式的梯度下降方程

$$线性回归方程\\w_{w,b}(x)=wx+b\\~---------------------\\ 代价函数\\J(w,b)=\frac1{2m}\sum_{i=1}^m (f_{w,b}(x_i)-y_i)^2\\~---------------------\\ 梯度下降算法\\ w=w-\alpha\frac\partial{\partial w}J(w,b)\\ b=w-\alpha\frac\partial{\partial b}J(w,b)\\~---------------------\\ 其中\\ 对w偏导数=\frac\partial{\partial w}J(w,b)=\frac 1m\sum_{i=1}^m(f_{w,b}(x_i)-y_i)x_i\\ 对b偏导数=\frac\partial{\partial b}J(w,b)=\frac 1m\sum_{i=1}^m(f_{w,b}(x_i)-y_i)~\\ （代价函数除以2的原因就是方便解这个导数）\\ （用复合函数求导就行，(f(g))'=f'(u)g'(x)）$$

即重复下式直到收敛

$$θ_0:=θ_0−α\frac 1m ∑^m_{i=1}(h_θ(x_i)−y_i)~~~~~~\\ θ_1:=θ_1−α\frac 1m ∑^m_{i=1}((h_θ(x_i)−y_i)x_i)$$

运行一下程序

这是一个根据房屋面积来预测价格的线性回归模型

其中m是训练集的大小，$\theta_{0}$是随着$\theta_{1}$和$x_ {i}$变化的常数，$y_ {i}$是给定训练集（数据）的值

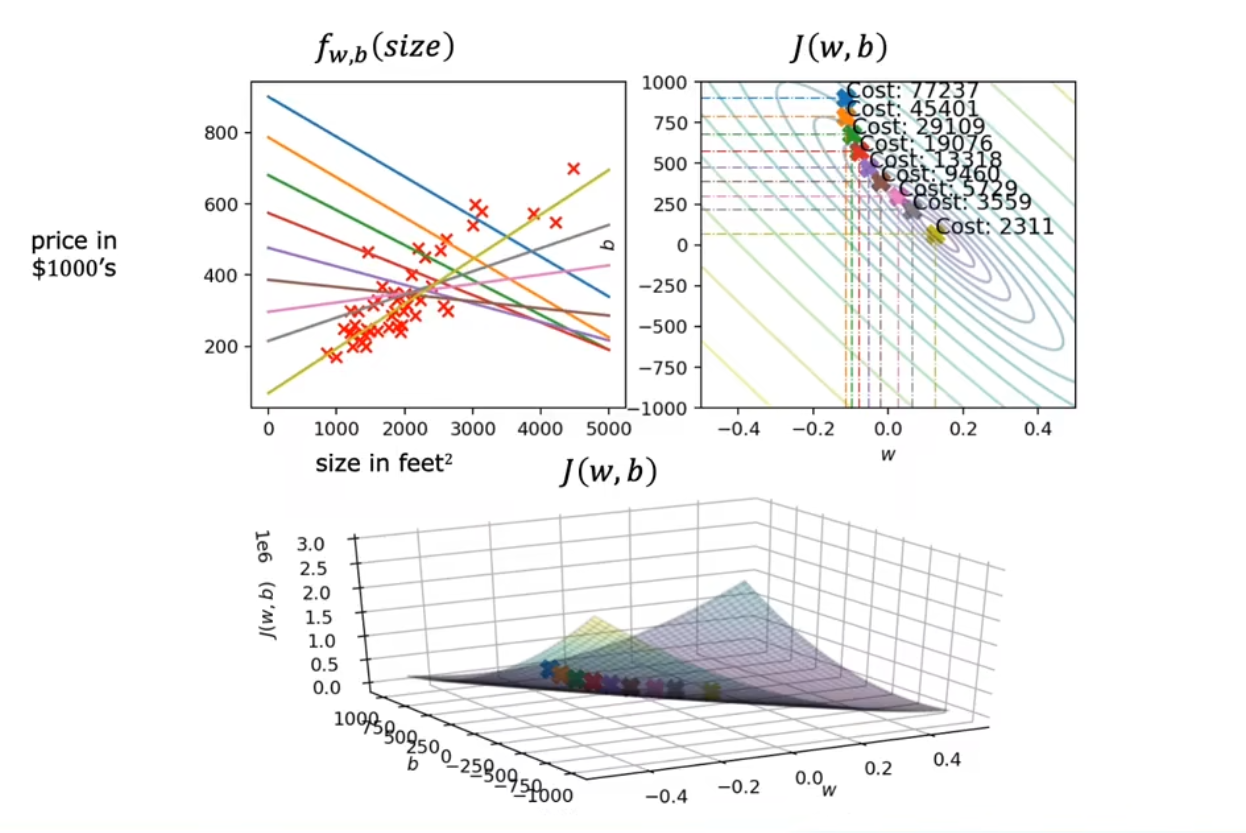
所有这些的要点是，如果我们从对假设的猜测开始，然后重复应用这些梯度下降方程，则我们的假设将变得越来越准确。