吴恩达机器学习
吴恩达机器学习
目录
其他补充
过拟合问题(Overfit)
过拟合问题
概念与总结
若拟合过低:我们称为 欠拟合(Underfit),也可以用另一个术语描述: 高偏差(High Bias)
例如你通常不能用一个线性回归模型或二阶多项式回归来拟合一个多项式回归模型
若拟合过高:我们称为 过拟合(Overfit),也可以用另一个术语描述:高方差(High Variance)。
或者称为 有泛化误差(Generalization Error)例如你通常不能用一个非常高阶的多项式回归模型来拟合数据
【用图来说明什么是过拟合问题】
这里用一个回归模型来举例:
(注意:图片中x的上标应该是指第几个特征,而不是幂,因为他的下标是用来标注第几条数据的)
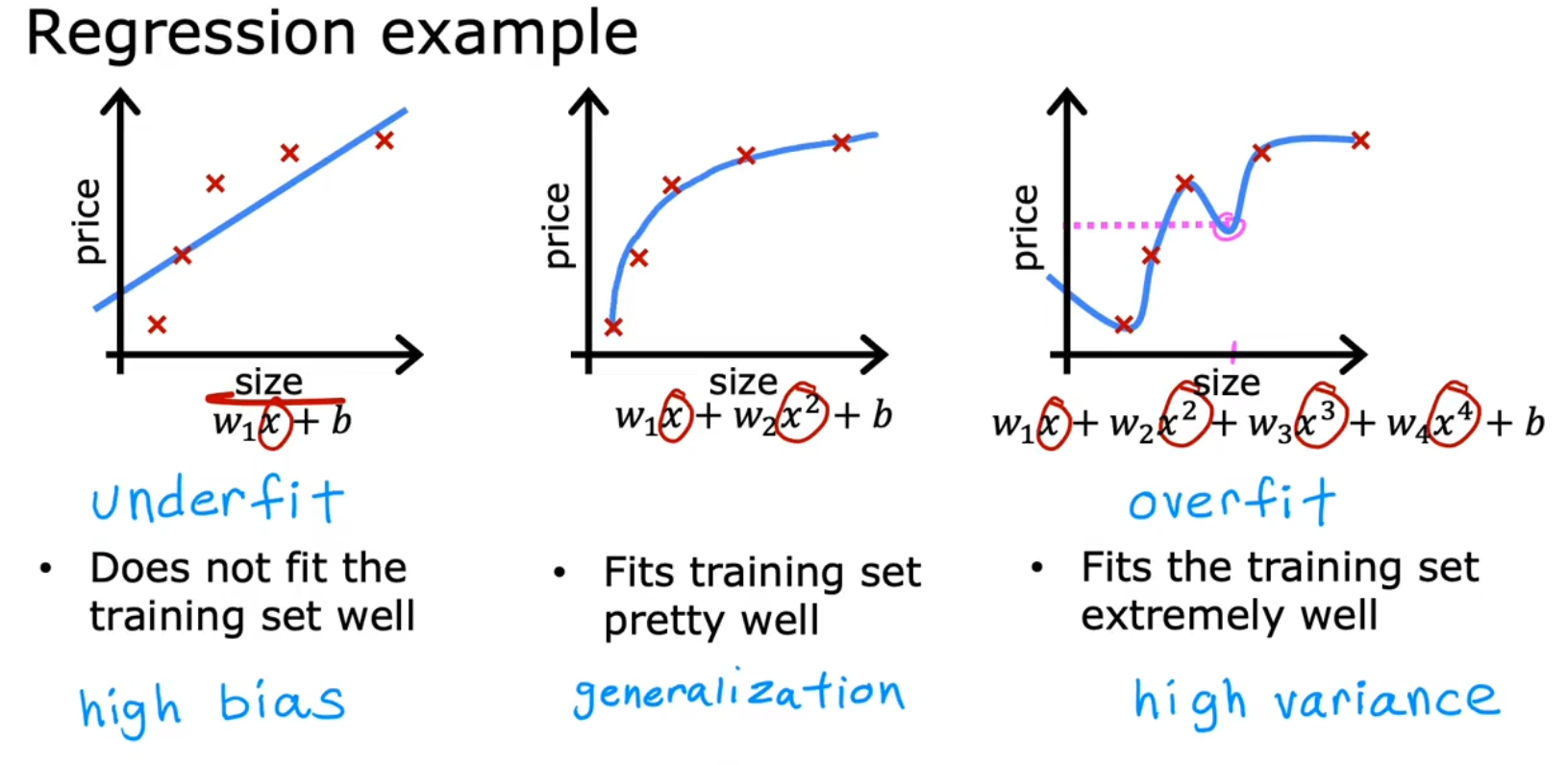
这里再用一个分类需求的模型来举例:
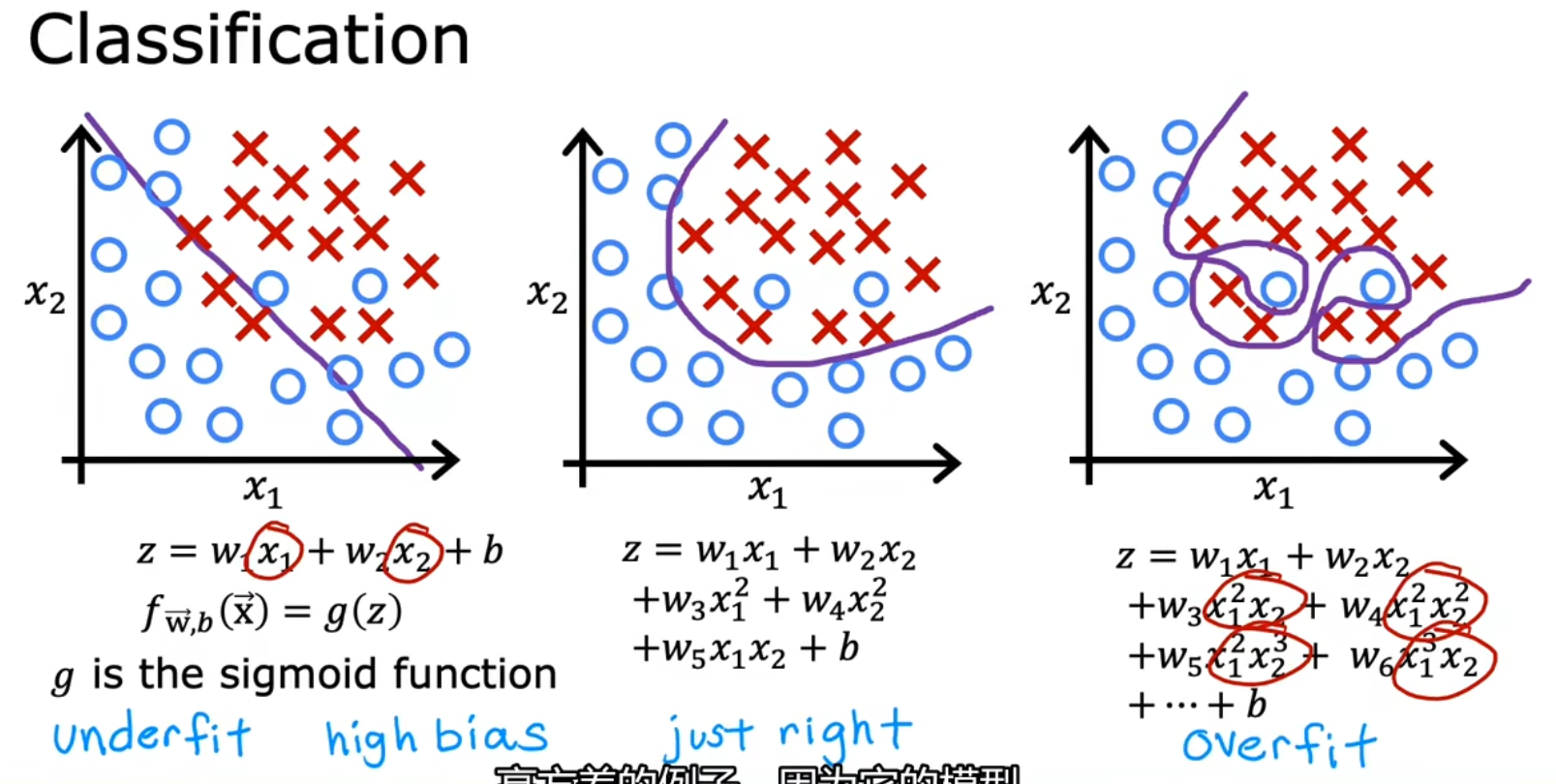
解决过拟合(三种方法)
解决方法
① 更多的训练数据(Collect more data)
② 使用更少的特征(Feature Selection)
不使用太高阶的多项式回归来拟合也是此类
比如本来需要用房屋的100个参数来预测,可以去除一些不必要的③ 正则化(Regularization,即 Reduce size of parameters)
与方法二相类似的,只是不会去剔除特征,而是会将该特征的权重降至极低。减少过拟合的程度
比较方法二和方法三:
(注意:图片中x的上标应该是指第几个特征,而不是幂,因为他的下标是用来标注第几条数据的)
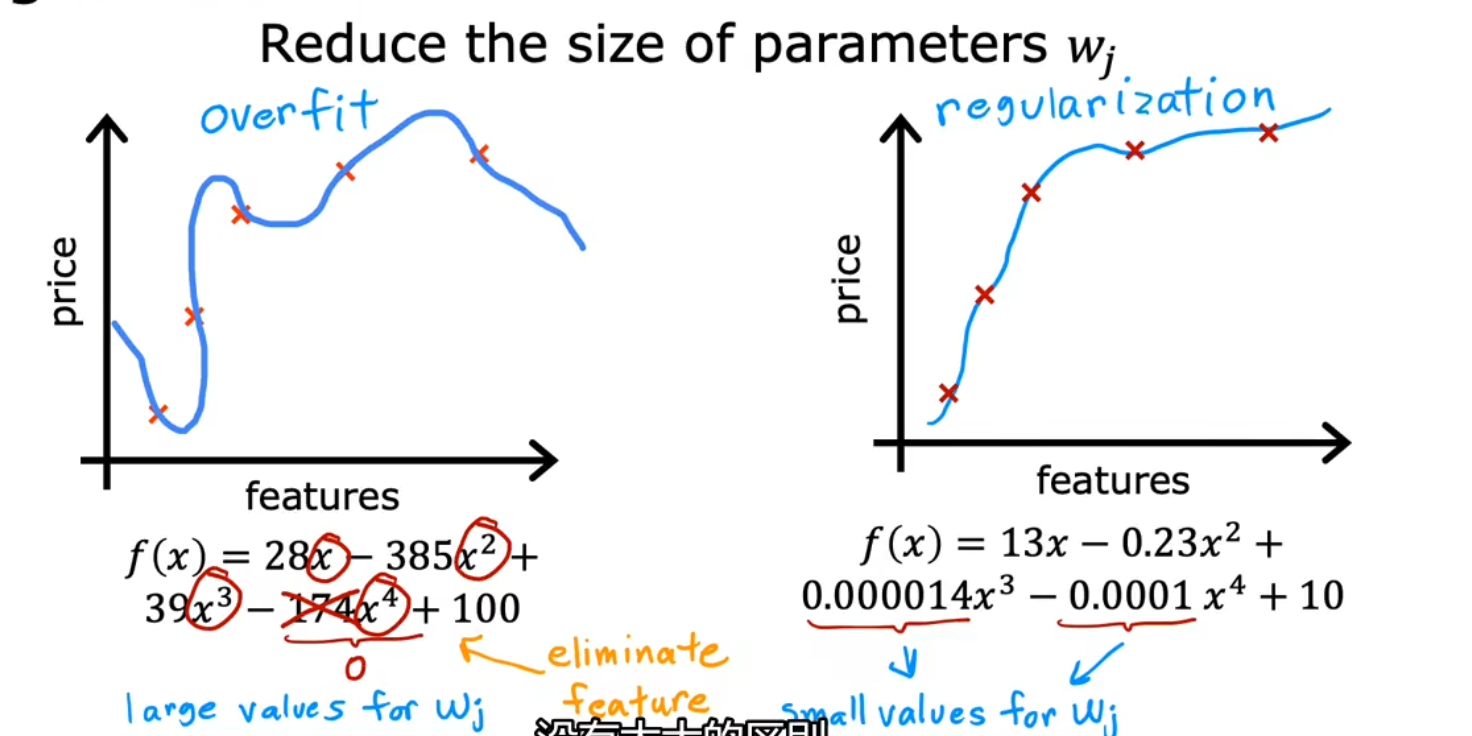
正则化(Regularization)
正则化方法
以回归模型为例:
~ \begin{align} 未正则化代价函数:J(\vec w,b)=&\frac{1}{2 m} \sum_{i=1}^{m}\left(f_{\vec w,b}\left(x_{i}\right)-y_{i}\right)^{2}\\ 正则化代价函数:J(\vec w,b)=&{\color{\orange}\frac{1}{2 m} \sum_{i=1}^{m}\left(f_{\vec w,b}\left(x_{i}\right)-y_{i}\right)^{2}} +{\color{red}\frac\lambda{2m}\sum^n_{j=1}w_j^2 +\frac\lambda{2m}b^2} \end{align}\\ ~\\
其中
- m 是训练数据的数量、n 是特征的数量
- 叫 正则化参数(regularizationparameter),且
- 的值设置越大,正则化代价函数右侧的权重就越高,w就越小。归一化程度越高
- 的值设置越小,正则化代价函数左侧的权重就越高,w就越大。拟合程度越高、越约容易过拟合
用于线性回归的正则方法
未正则化的梯度下降
未正则化代价函数:\\ J(\vec w,b)={\color{\orange}\frac{1}{2 m} \sum_{i=1}^{m}\left(f_{\vec w,b}\left(x_{i}\right)-y_{i}\right)^{2}}\\~\\ 未正则化的梯度下降:\\ \begin{align} w_j:=&w_j-\alpha\frac\partial{\partial w_j}J(\vec w,b) &&=w_j-\alpha\frac 1m\sum_{i-1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ b:=&b-\alpha\frac\partial{\partial b}J(\vec w,b) &&=b-\alpha\frac 1m\sum_{i-1}^m(f_{\vec w,b}(\vec x_i)-y_i)\\ \end{align}
正则化后的梯度下降
正则化代价函数:\\ J(\vec w,b)={\color{\orange}\frac{1}{2 m} \sum_{i=1}^{m}\left(f_{\vec w,b}\left(x_{i}\right)-y_{i}\right)^{2}} +{\color{red}\frac\lambda{2m}\sum^n_{j=1}w_j^2}\\~\\ 梯度下降:\\ \begin{align} w_j:=&w_j-\alpha\frac\partial{\partial w_j}J(\vec w,b) &&=w_j-\alpha[\frac 1m\sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}+{\color{red}\frac\lambda m w_j}]\\ &&&=w_j-\alpha\frac\lambda m w_j-\alpha\frac1m \sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ &&&={\color{red}w_j(1-\alpha\frac\lambda m)}-\alpha\frac1m \sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ b:=&b-\alpha\frac\partial{\partial b}J(\vec w,b) &&=b-\alpha[\frac 1m\sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)]\\ \end{align}
用于逻辑回归的正则方法
逻辑回归的梯度下降“看起来”是和线性回归差不多的,正则化了也是
正则化后的梯度下降
正则化代价函数:\\ J(\vec w,b)={\color{\orange}\frac{1}{m} \sum_{i=1}^{m} \left[y_i\log\left(f_{\vec w,b}(x_i)\right)+(1-y_i)\log\left(1-f_{\vec w,b}(x_i)\right)\right]} +{\color{red}\frac\lambda{2m}\sum^n_{j=1}w_j^2}\\~\\ 梯度下降:\\ \begin{align} w_j:=&w_j-\alpha\frac\partial{\partial w_j}J(\vec w,b) &&=w_j-\alpha[\frac 1m\sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}+{\color{red}\frac\lambda m w_j}]\\ &&&={\color{red}w_j(1-\alpha\frac\lambda m)}-\alpha\frac1m \sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ b:=&b-\alpha\frac\partial{\partial b}J(\vec w,b) &&=b-\alpha[\frac 1m\sum_{i=1}^m(f_{\vec w,b}(\vec x_i)-y_i)]\\ \end{align}
程序示例
见神经网络一章的优化一节