跳至主要內容

吴恩达机器学习

吴恩达机器学习

目录

多变量线性回归模型（Linear Regression）

多维特征

输入变量也叫特征，多维特征即多个输入变量

例如

房屋面积卧室数层数房屋年龄价格
21045145460
14163240232
15343230315
8522136178
…………………………

符号表示

xj=jth 特征n=特征的数量x⃗i=第i个训练示例的特征\begin{align} x_j=&j^{th}~特征\\ n=&特征的数量\\ \vec x^i=&第i个训练示例的特征 \end{align}

模型公式

单变量：fw,b(x)=wx+b多变量：fw,b(x)=w1x1+w2x2+w3x3+⋯+b\begin{align} 单变量：f_{w,b}(x)=&wx+b\\ 多变量：f_{w,b}(x)=&w_1x_1+w_2x_2+w_3x_3+\dots+b \end{align}

用 向量化 化简后的模型公式

令 w⃗=[w1w2w3…wn]T令 x⃗=[x1x2x3…xn]Tfw⃗,b(x⃗)=w⃗⋅x⃗+b（点乘，如果是叉乘也行，加个转置）令~\vec w=\begin{bmatrix}w_1&w_2&w_3&\dots&w_n\end{bmatrix}^T\\ 令~\vec x=\begin{bmatrix}x_1&x_2&x_3&\dots&x_n\end{bmatrix}^T\\ f_{\vec w,b}(\vec x)=\vec w \cdot \vec x+b\\ （点乘，如果是叉乘也行，加个转置）

向量化

向量化可以去除for循环，并节省几百倍的时间。
特别是这种循环计算item并sum+=item的类型，一般都可以去并行化。像很多语言的 “高级循环” 语句，都是相似的原理
例如 js 的 reduce等三种高级循环

对比向量化和非向量化的时间差异（点乘）

import numpy as np 			# 导入numpy库
a = np.array([1,2,3,4]) 	# 创建一个数据a
print(a)					# 结果：[1 2 3 4]

import time 				# 导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) # 通过round随机得到两个一百万维度的数组
tic = time.time() 			# 现在测量一下当前时间

# 向量化的版本
c = np.dot(a,b)
toc = time.time()
print("Vectorized version:" + str(1000*(toc-tic)) +"ms") 	# 打印一下向量化的版本的时间。结果：1.5027ms

# 非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
print(c)
print("For loop:" + str(1000*(toc-tic)) + "ms") 			# 打印for循环的版本的时间。结果：474.2951ms

NumPy库

NumPy库介绍

比Python自身的嵌套列表（nested list structure)结构要高效的多（该结构也可以用来表示矩阵（matrix）），
支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库

代码实现，用的NumPy工具

w = np.array([1.0, 2.5, -3.3])	# 访问方法：w[i]
b = 4
x = np.array([10, 20, 30])		# 访问方法：x[i]

f = np.dot(w,x)+b				# 向量化的一个好处是快，对于大数据还可以多线程并行工作，而不是单线程循环

用于多变量线性回归的梯度下降法

未向量化写法

参数：w1,⋯ ,wn,b模型：fw,b(x)=w1x1+w2x2+w3x3+⋯+b代价函数：J(w1,⋯ ,wn,b)梯度下降法：wj:=wj−α∂∂wjJ(w1,⋯ ,wn,b)b:=b−α∂∂bJ(w1,⋯ ,wn,b)\begin{align} 参数：&w_1,\cdots,w_n,b\\ 模型：&f_{w,b}(x)=w_1x_1+w_2x_2+w_3x_3+\dots+b\\ 代价函数：&J(w_1,\cdots,w_n,b)\\ 梯度下降法：&w_j:=w_j-\alpha\frac\partial{\partial w_j}J(w_1,\cdots,w_n,b)\\ &b:=b-\alpha\frac\partial{\partial b}J(w_1,\cdots,w_n,b)\\ \end{align}

向量化写法

参数：w⃗,b模型：fw,b(x)=w⃗⋅x⃗+b代价函数：J(w⃗,b)=12m∑i=1m(fw⃗,b(x(i))−y(i))2梯度下降法：wj:=wj−α∂∂wjJ(w⃗,b)b:=b−α∂∂bJ(w⃗,b)\begin{align} 参数：&\vec w,b\\ 模型：&f_{w,b}(x)=\vec w\cdot \vec x+b\\ 代价函数：&J(\vec w,b)=\frac{1}{2 m} \sum_{i=1}^{m}\left(f_{\vec w,b}\left(x_{(i)}\right)-y_{(i)}\right)^{2}\\ 梯度下降法：&w_j:=w_j-\alpha\frac\partial{\partial w_j}J(\vec w,b)\\ &b:=b-\alpha\frac\partial{\partial b}J(\vec w,b)\\ \end{align}

推导化简得

wj:=wj−α∂∂wjJ(w⃗,b)=wj−α1m∑i−1m(fw⃗,b(x⃗i)−yi)xijb:=b−α∂∂bJ(w⃗,b)=b−α1m∑i−1m(fw⃗,b(x⃗i)−yi)\begin{align} w_j:=&w_j-\alpha\frac\partial{\partial w_j}J(\vec w,b)\\ =&w_j-\alpha\frac 1m\sum_{i-1}^m(f_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ b:=&b-\alpha\frac\partial{\partial b}J(\vec w,b)\\ =&b-\alpha\frac 1m\sum_{i-1}^m(f_{\vec w,b}(\vec x_i)-y_i) \end{align}

与单变量线性回归相比

公式上用的点乘，化简起来和单变量线性回归一样，不算复杂

未知量的值更多，本来可以看作是θ0、θ1\theta_0、\theta_1，现在变成了θ0、θ1、⋯、θn\theta_0、\theta_1、\cdots、\theta_n

特征缩放

望文生义的错误意思：

有点类似于加权的意思，fw,b(x)=w1x1+w2x2+w3x3+⋯+bf_{w,b}(x)=w_1x_1+w_2x_2+w_3x_3+\dots+b中，w1,w2,⋯ ,wnw_1,w_2,\cdots,w_n会乘以输入变量，即乘以“特征”。也称为特征缩放

其实是为了方便画图来进行的缩放，平均归一化（normalization）。一般将他们的点限制在[(−1,−1),(1,1)][(-1,-1),(1,1)]的二维作用域当中

例如：

对于x1的取值范围：300≤x1≤2000，平均值μ1令 x1:=x1−μ12000−300，则−0.18≤x1≤0.82 对于x2的取值范围：      0≤x2≤5    ，平均值μ2令 x1:=x2−μ25−0，则−0.46≤x1≤0.54对于x_1的取值范围：300\leq x_1 \leq 2000，平均值\mu_1\\ 令~x_1:=\frac{x_1-\mu_1}{2000-300}，则-0.18\leq x_1\leq 0.82\\~\\ 对于x_2的取值范围：~~~~~~0\leq x_2 \leq 5~~~~，平均值\mu_2\\ 令~x_1:=\frac{x_2-\mu_2}{5-0}，则-0.46\leq x_1\leq 0.54

翻译问题

Z-score normalization，Z方向的的缩放归一化

特征工程（Feature Engineering）

参考：【知乎】特征工程简介（内容其实挺多的，这里省略，详见链接）

  • 特征工程概念
    • 是指用一系列工程化的方式从原始数据中筛选出更好的数据特征，以提升模型的训练效果
      是机器学习中不可或缺的一部分
    • 业内有一句广为流传的话是：数据和特征决定了机器学习的上限，而模型和算法是在逼近这个上限而已
    • 特征工程通常包括数据预处理、特征选择、降维等环节。如下图所示img
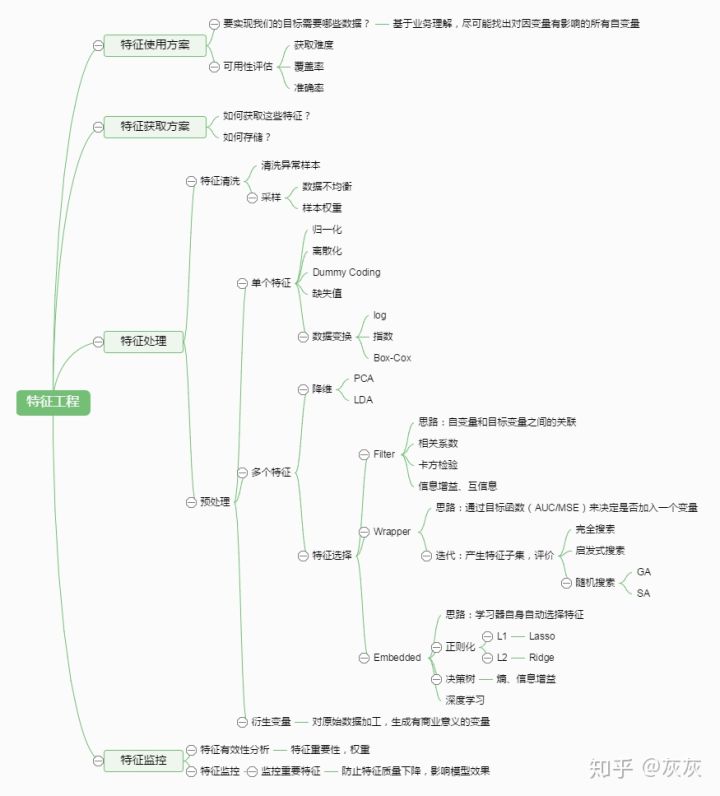
  • 例如
    • 通过房屋的frontage长度和depth深度来估算价格，而不是仅通过area面积。这就是一种对特征选择的优化
链接到当前文件 0
没有文件链接到当前文件