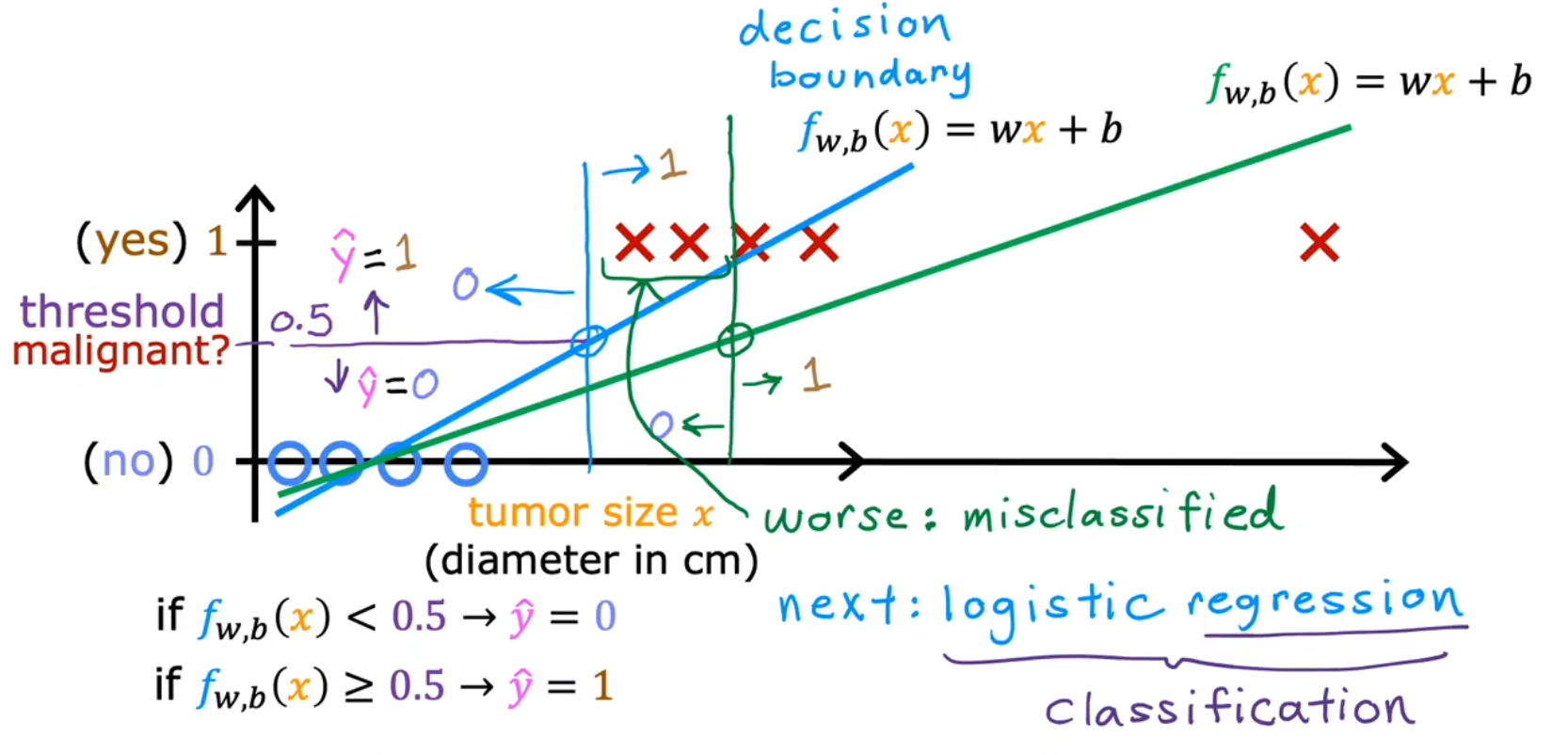
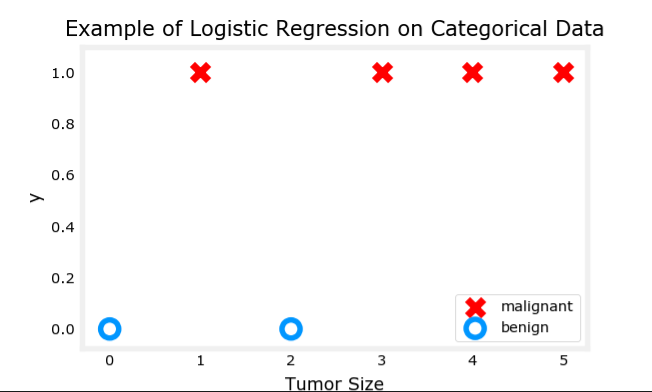
吴恩达机器学习 目录 逻辑回归模型(Logistic Regression)逻辑回归 动机与目的 作用:可以用于解决分类问题。之前说的线性回归和多项式回归则是解决预测问题,而不能解决分类问题 例如:找出邮件是否广告、预测肿瘤是恶性还是良性 补充 如果分类只有两种,比如回答是或不是,则称之为二元分类 (Binary Classification) 单/多变量逻辑回归 ① 模型定义 - Sigmoid函数 图像 不能用线性回归模型来解决监督模型的分类问题
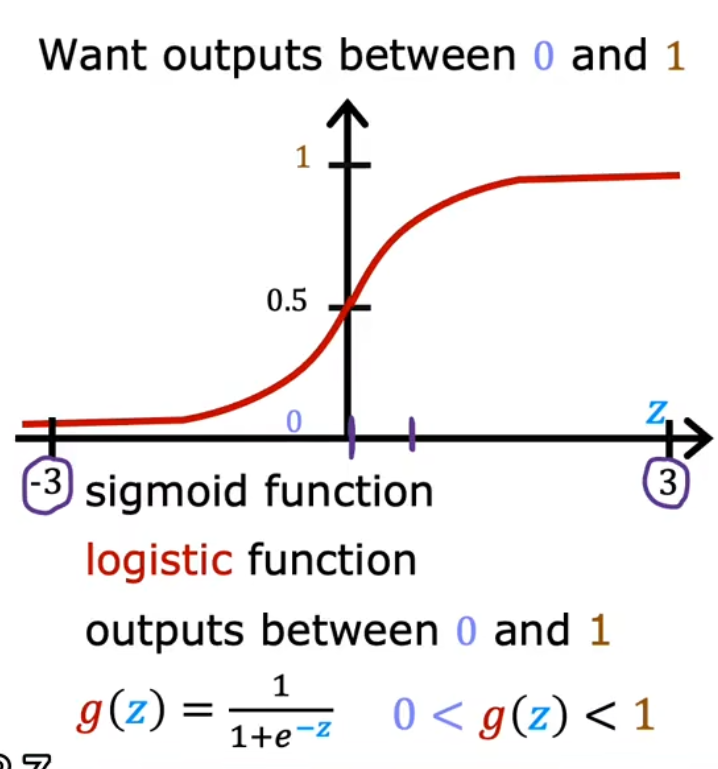
一般用数学的Sigmoid函数来构建逻辑回归模型
公式 Sigmoid函数
g ( z ) = 1 1 + e − z , g ( z ) ⊂ ( 0 , 1 ) z = w ⃗ ⋅ x ⃗ + b g(z)=\frac{1}{1+e^{-z}},~g(z)\sub (0,1)\\ z=\vec w\cdot\vec x+b g ( z ) = 1 + e − z 1 , g ( z ) ⊂ ( 0 , 1 ) z = w ⋅ x + b
结合模型得到逻辑函数 (logistic function)
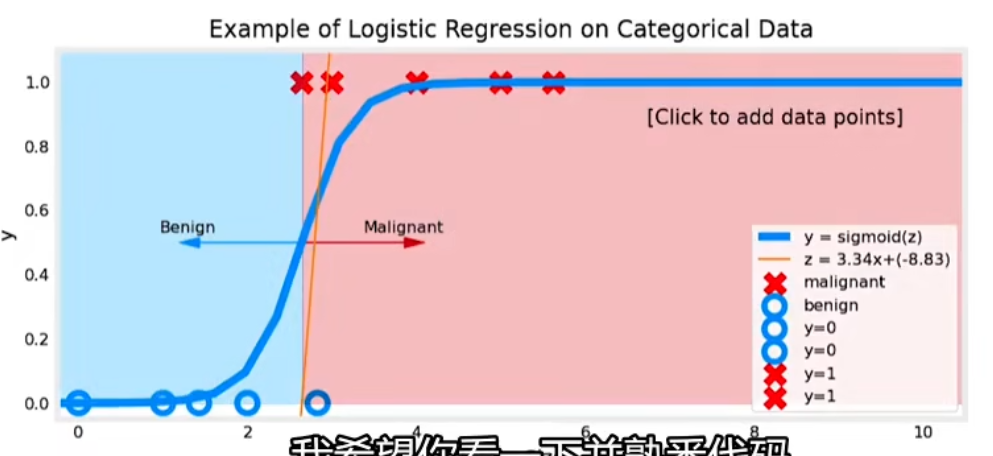
令 z = w ⃗ ⋅ x ⃗ + b 得到逻辑函数 : f w ⃗ , b ( x ⃗ ) = g ( w ⃗ ⋅ x ⃗ + b ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) = P ( y = 1 ∣ x ; w ⃗ , b ) 其中: z 换元是为了偏移和缩放,令 z ⊂ [ 0 , + ∞ ) 和图像美观 x 是肿瘤大小 y 轴中是 0 表示肿瘤良性、 1 表示肿瘤为恶性 P 是得到 1 个概率 , y 是 0.7 则表示肿瘤有 70 % 可能是恶性 令~z=\vec w\cdot\vec x+b\\ 得到逻辑函数:\\ f_{\vec w,b}(\vec x)=g(\vec w\cdot \vec x+b)=\frac 1{1+e^{-(\vec w\cdot \vec x+b)}}\\=P(y=1|x;\vec w,b) \\~\\ 其中:\\ z换元是为了偏移和缩放,令z\sub[0,+\infty)和图像美观\\ x是肿瘤大小\\y轴中是0表示肿瘤良性、1表示肿瘤为恶性\\ P是得到1个概率,y是0.7则表示肿瘤有70\%可能是恶性 令 z = w ⋅ x + b 得到逻辑函数 : f w , b ( x ) = g ( w ⋅ x + b ) = 1 + e − ( w ⋅ x + b ) 1 = P ( y = 1∣ x ; w , b ) 其中: z 换元是为了偏移和缩放,令 z ⊂ [ 0 , + ∞ ) 和图像美观 x 是肿瘤大小 y 轴中是 0 表示肿瘤良性、 1 表示肿瘤为恶性 P 是得到 1 个概率 , y 是 0.7 则表示肿瘤有 70% 可能是恶性
代码 代码运行结果
【概念补充】决策边界(Decision Boundary) 算法:根据Z=0时算出来的,Z=0时,即表示在Sigmoid函数的中间部分
单参数线性逻辑回归 的决策边界 (这个图也可以画成一维的。将该图y轴缩小无限倍 坍塌成线即可,此时决策边界是一个点)
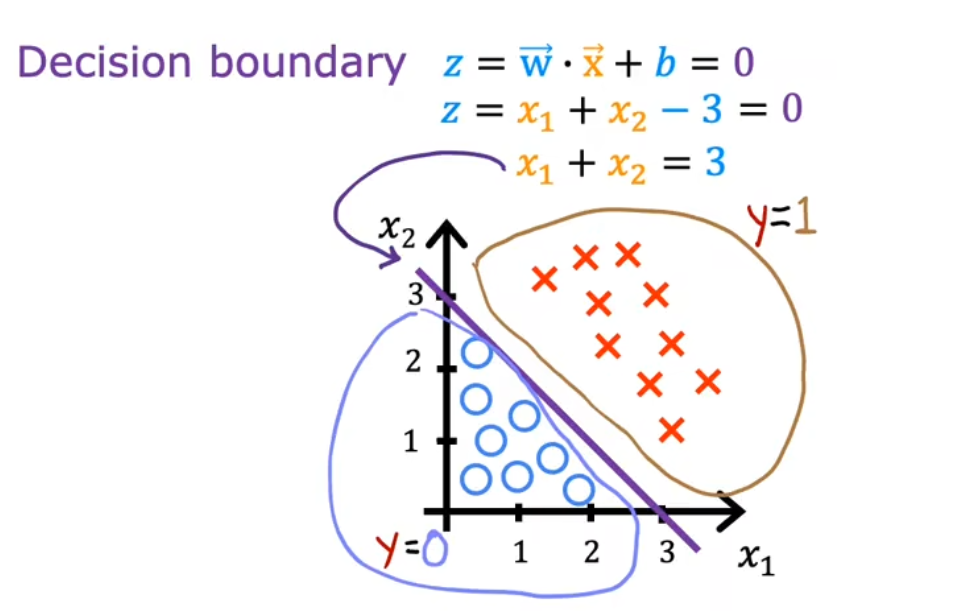
二线性元逻辑回归 的决策边界
二元非线性逻辑回归 的决策边界
椭圆和其他形状的决策边界也同理
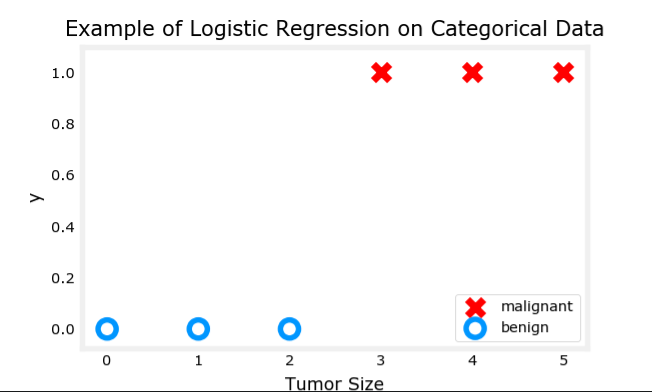
② 逻辑回归中的Loss函数 这是一个二元逻辑回归的训练集
肿瘤大小 cm 患者的年龄 是否恶性 10 52 1 2 73 0 5 55 0 12 49 1 …… …… ……
为什么不用平方误差代价函数 Q:能否用平方误差作为代价函数?
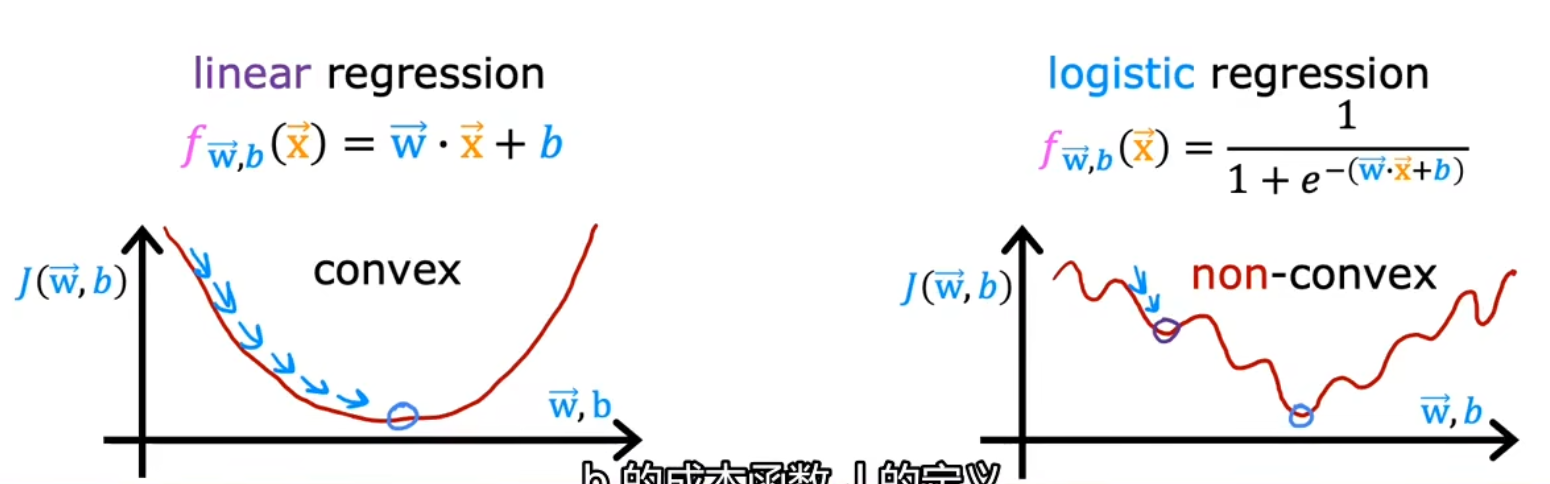
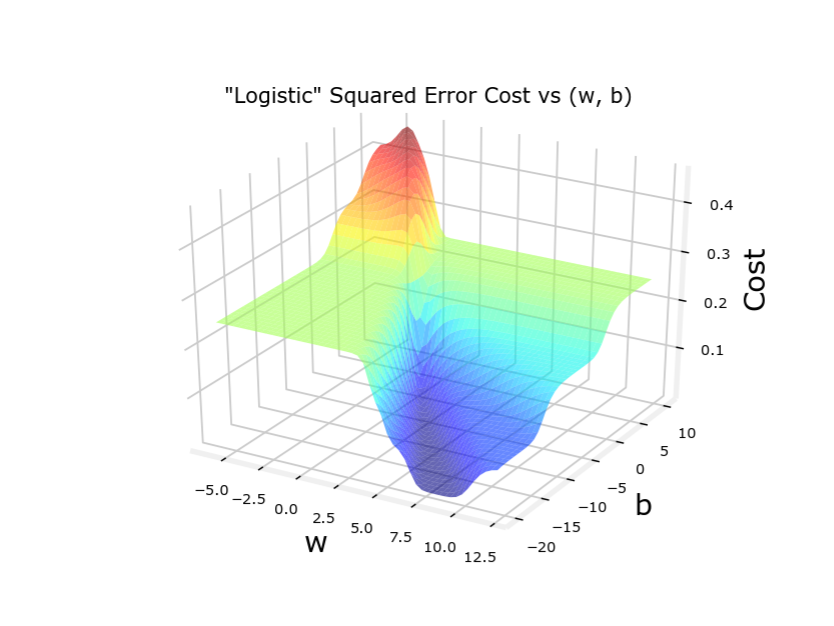
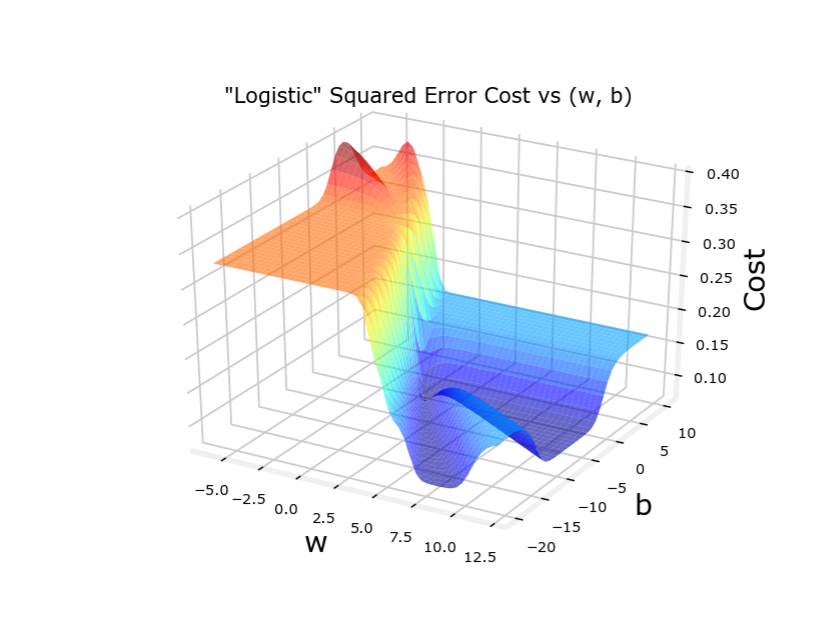
线性回归模型一般用平方误差代价函数: J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x i ) − y i ) 2 该代价函数是凸函数( c o n v e x ),能用梯度下降来最优化 但是如果代价回归函数也用平方误差代价函数,其代价函数不是凸函数,有多个极小值 线性回归模型一般用平方误差代价函数:\\ J\left(w, b\right)= \frac{1}{2 m} \sum_{i=1}^{m}\left(f_{w,b}\left(x_{i}\right)-y_{i}\right)^{2}\\ 该代价函数是凸函数(convex),能用梯度下降来最优化\\ 但是如果代价回归函数也用平方误差代价函数,其代价函数不是凸函数,有多个极小值 线性回归模型一般用平方误差代价函数: J ( w , b ) = 2 m 1 i = 1 ∑ m ( f w , b ( x i ) − y i ) 2 该代价函数是凸函数( co n v e x ),能用梯度下降来最优化 但是如果代价回归函数也用平方误差代价函数,其代价函数不是凸函数,有多个极小值
新Loss函数(分段版)公式 我们需要一个Loss函数
L o s s : L ( f w ⃗ , b ( x i ) , y i ) L o s s 函数以预测值和实际值作为输入,输出损失值 L 例如:在平方误差代价函数中: L ( f w ⃗ , b ( x i ) , y i ) = ( f w ⃗ , b ( x i ) − y i ) 2 Loss:L(f_{\vec w,b}(x_i),y_i)\\ Loss函数以预测值和实际值作为输入,输出损失值L\\~\\ 例如:在平方误差代价函数中:\\ L(f_{\vec w,b}(x_i),y_i)=(f_{\vec w,b}(x_i)-y_i)^2 L oss : L ( f w , b ( x i ) , y i ) L oss 函数以预测值和实际值作为输入,输出损失值 L 例如:在平方误差代价函数中: L ( f w , b ( x i ) , y i ) = ( f w , b ( x i ) − y i ) 2
我们最好能找到一个新的Loss函数,使代价函数变成凸函数,以便于收敛 找最优值
逻辑函数的Loss函数如下
L ( f w ⃗ , b ( x i ) , y i ) = { − log ( f w ⃗ , b ( x ⃗ i ) ) if y i = 1 − log ( 1 − f w ⃗ , b ( x ⃗ i ) ) if y i = 0 L(f_{\vec w,b}(x_i),y_i)= \begin{cases} -\log(~~~~~~f_{\vec w,b}(\vec x_i)) & \text{ if } y_i= 1\\ -\log(1-f_{\vec w,b}(\vec x_i)) & \text{ if } y_i= 0 \end{cases} L ( f w , b ( x i ) , y i ) = { − log ( f w , b ( x i )) − log ( 1 − f w , b ( x i )) if y i = 1 if y i = 0
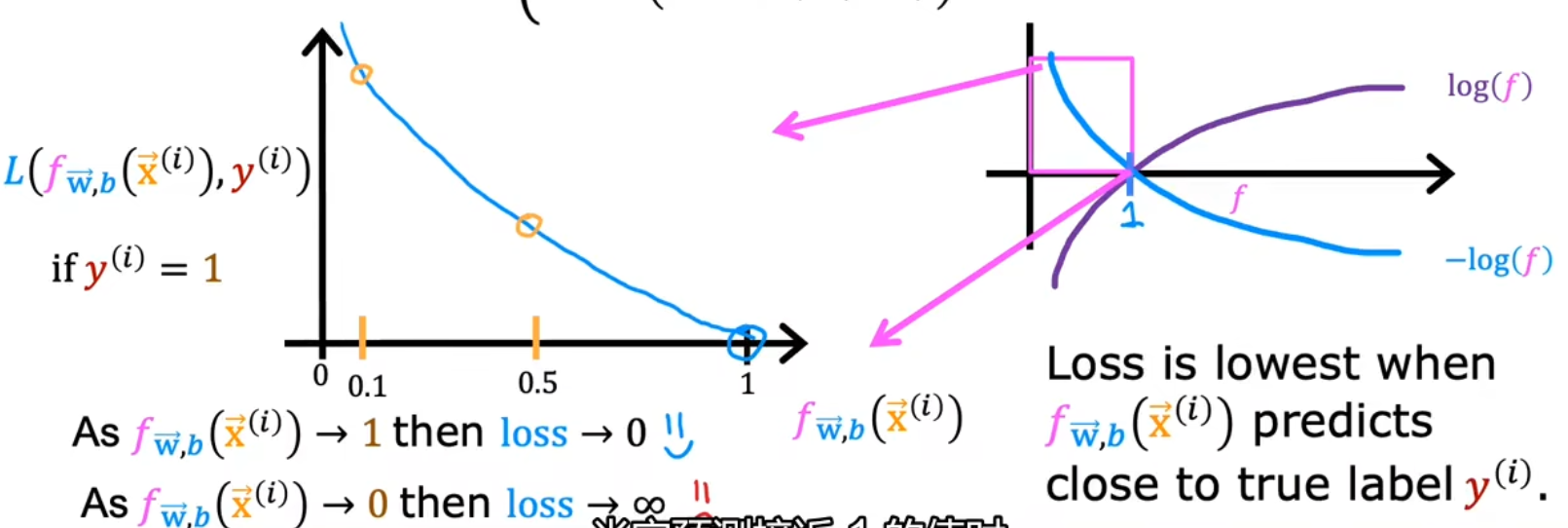
新Loss函数(分段版)图像 蓝线部分是Loss函数的图像,根据实际值不同会有两个图像。横轴是预测值,纵轴是代价
当y i = 1 y_i=1 y i = 1
公式:L ( f w ⃗ , b ( x i ) ) = − log ( f w ⃗ , b ( x ⃗ i ) ) L(f_{\vec w,b}(x_i))=-\log(f_{\vec w,b}(\vec x_i)) L ( f w , b ( x i )) = − log ( f w , b ( x i ))
若f ( x i ) = 0.001 f(x_i)=0.001 f ( x i ) = 0.001
若f ( x i ) = 1 f(x_i)=1 f ( x i ) = 1
图像如下
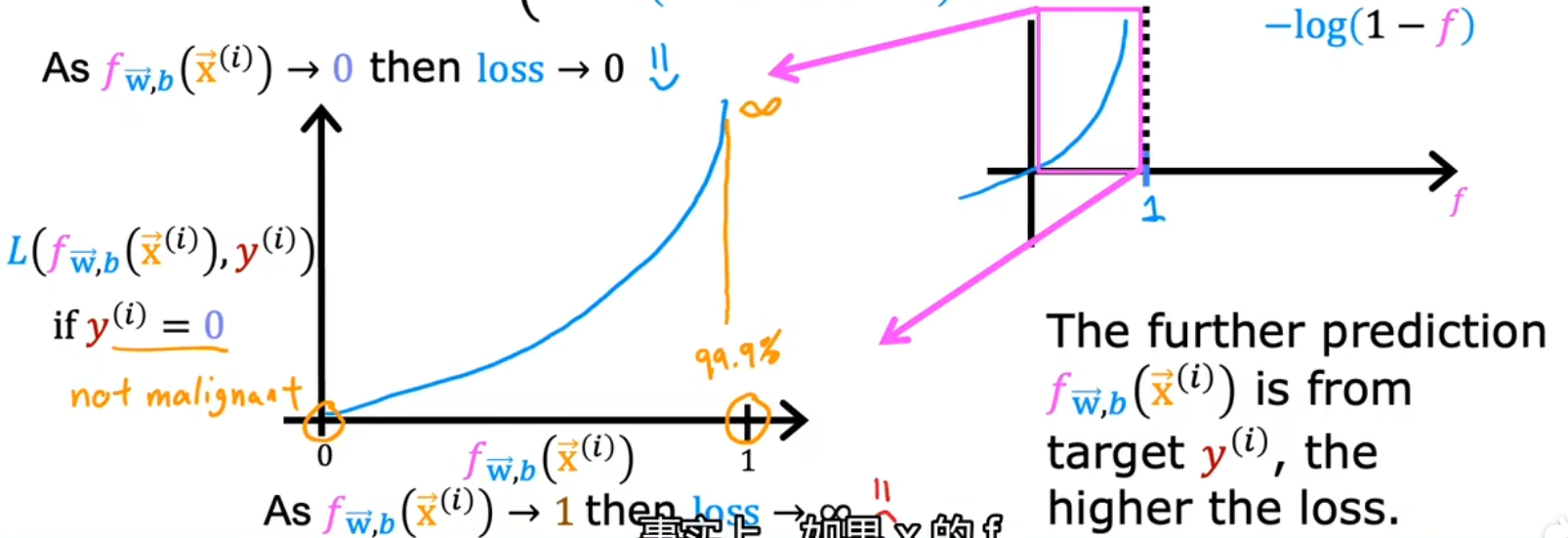
当y i = 0 y_i=0 y i = 0
公式:L ( f w ⃗ , b ( x i ) ) = − log ( 1 − f w ⃗ , b ( x ⃗ i ) ) L(f_{\vec w,b}(x_i))=-\log(1-f_{\vec w,b}(\vec x_i)) L ( f w , b ( x i )) = − log ( 1 − f w , b ( x i ))
若f ( x i ) = 0.001 f(x_i)=0.001 f ( x i ) = 0.001
若f ( x i ) = 0 f(x_i)=0 f ( x i ) = 0
图像如下
新Loss函数(单公式)公式 简化Loss函数(Simplified Loss Function)
原 L o s s 函数 L ( f w ⃗ , b ( x i ) , y i ) = { − log ( f w ⃗ , b ( x ⃗ i ) ) if y i = 1 − log ( 1 − f w ⃗ , b ( x ⃗ i ) ) if y i = 0 简化版 L o s s 函数 L ( f w ⃗ , b ( x i ) , y i ) = − y i log ( f w ⃗ , b ( x ⃗ i ) ) − ( 1 − y i ) log ( 1 − f w ⃗ , b ( x ⃗ i ) ) 其实就是省略了条件判断 当 y = 0 ,红色部分为 0 ;当 y = 1 ,橙色部分为 0 原Loss函数\\ L(f_{\vec w,b}(x_i),y_i)= \begin{cases} \color{red}-\log(~~~~~~f_{\vec w,b}(\vec x_i)) & \text{ if } y_i= 1\\ \color{orange}-\log(1-f_{\vec w,b}(\vec x_i)) & \text{ if } y_i= 0 \end{cases} \\~\\ 简化版Loss函数\\ L(f_{\vec w,b}(x_i),y_i)= \color{red}{-y_i\log(f_{\vec w,b}(\vec x_i))} \color{orange}{-(1-y_i)\log(1-f_{\vec w,b}(\vec x_i))} \\~\\ 其实就是省略了条件判断\\当y=0,红色部分为0;当y=1,橙色部分为0 原 L oss 函数 L ( f w , b ( x i ) , y i ) = { − l o g ( f w , b ( x i )) − l o g ( 1 − f w , b ( x i )) if y i = 1 if y i = 0 简化版 L oss 函数 L ( f w , b ( x i ) , y i ) = − y i l o g ( f w , b ( x i )) − ( 1 − y i ) l o g ( 1 − f w , b ( x i )) 其实就是省略了条件判断 当 y = 0 ,红色部分为 0 ;当 y = 1 ,橙色部分为 0
新Loss函数(单公式)图像 这L ( f w ⃗ , b ( x i ) , y i ) L(f_{\vec w,b}(x_i),y_i) L ( f w , b ( x i ) , y i ) y i = 0 / 1 y_i=0/1 y i = 0/1
② 逻辑回归中的代价函数 公式 简化代价函数(Simplified Cost Function)
简化完Loss函数后,代入回代价函数中:
J ( w ⃗ , b ) = 1 m ∑ i = 1 m [ L ( f w ⃗ , b ( x i ) , y i ) ] = − 1 m ∑ i = 1 m [ + y i log ( f w ⃗ , b ( x ⃗ i ) ) + ( 1 − y i ) log ( 1 − f w ⃗ , b ( x ⃗ i ) ) ] \begin{align} J(\vec w,b)=&~~~\frac1m\sum^m_{i=1}[ L(f_{\vec w,b}(x_i),y_i) ]\\ =&{\color{red}-}\frac1m\sum^m_{i=1}[ {\color{red}+y_i\log(f_{\vec w,b}(\vec x_i))} {\color{orange}+(1-y_i)\log(1-f_{\vec w,b}(\vec x_i))} ] \end{align} J ( w , b ) = = m 1 i = 1 ∑ m [ L ( f w , b ( x i ) , y i )] − m 1 i = 1 ∑ m [ + y i l o g ( f w , b ( x i )) + ( 1 − y i ) l o g ( 1 − f w , b ( x i )) ]
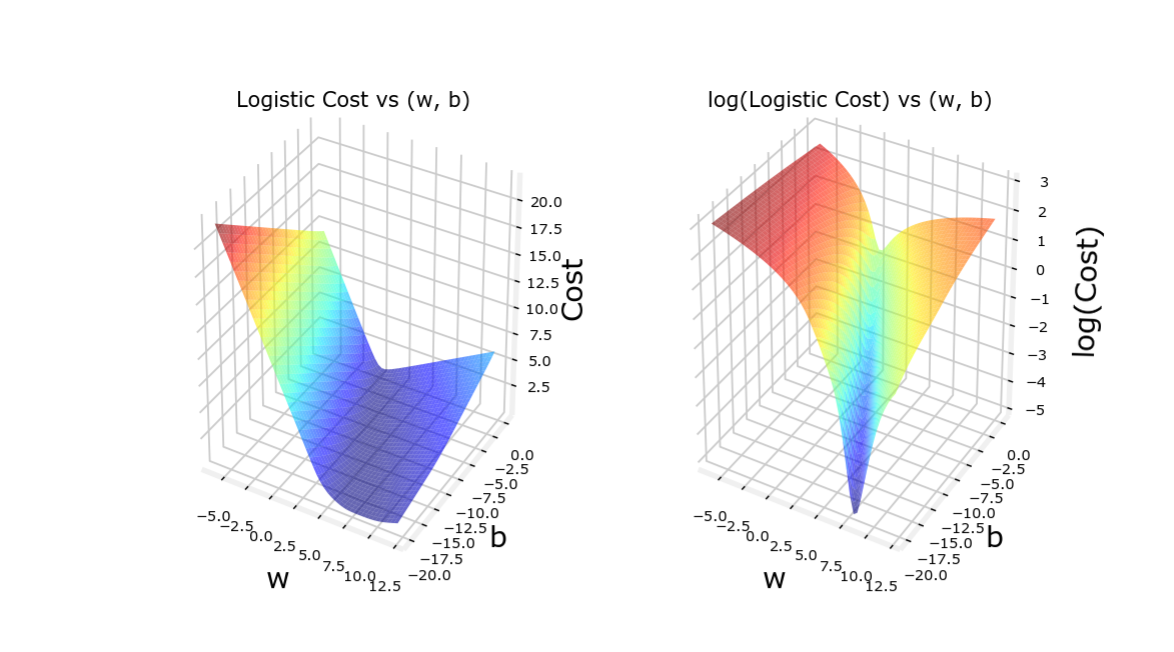
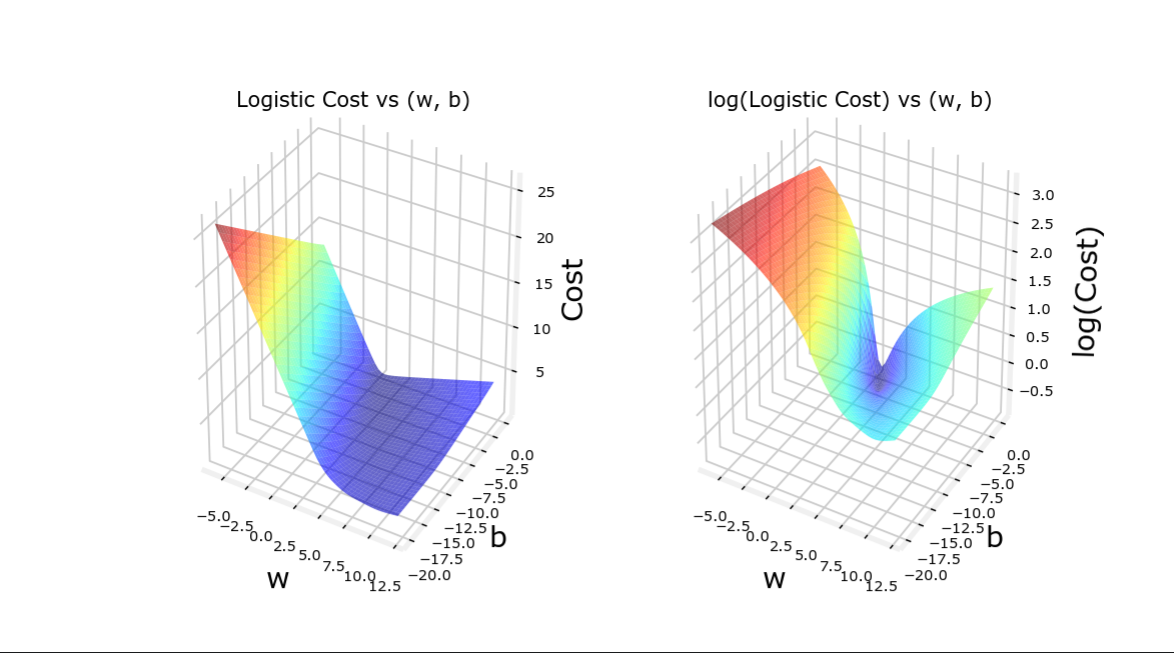
图像 通过新的Loss函数,代价函数是凸函数,此时可以使用梯度下降方法
代价函数图像如下,顺便比较平均误差代价函数
训练集1(符合得较好) 训练集2(符合得较差) 训练集------ 平均误差代价函数 逻辑回归代价函数
(一旦预测训练集与回归模型符合得不好,平均误差代价函数就会出问题)
③ 梯度下降 实现 代价函数: J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ − y i log ( f w ⃗ , b ( x ⃗ i ) ) − ( 1 − y i ) log ( 1 − f w ⃗ , b ( x ⃗ i ) ) ] 梯度下降求偏导: w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = w j − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ i ) − y i ) x i j b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α 1 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ i ) − y i ) 看上去和线性回归函数一样,但要注意的是这里的 f 的含义不同,这里的 f 是逻辑回归 L i n e a r r e g r e s s i o n : f w ⃗ , b ( x ) = w ⃗ ⋅ x ⃗ + b L o g i s t i c r e g r e s s i o n : f w ⃗ , b ( x ) = 1 1 + e − z 代价函数:\\ {\color{red}J(\vec w,b)}=-\frac1m\sum^m_{i=1}[ -y_i\log(f_{\vec w,b}(\vec x_i)) -(1-y_i)\log(1-f_{\vec w,b}(\vec x_i)) ]\\~\\ 梯度下降求偏导:\\ \begin{align} w_j=&w_j-\alpha\frac\partial{\partial w_j}{\color{red}J(\vec w,b)}\\ =&w_j-\alpha\frac1m\sum_{i=1}^m({\color{orange}f}_{\vec w,b}(\vec x_i)-y_i)x_{ij}\\ b=&b-\alpha\frac\partial{\partial b}{\color{red}J(\vec w,b)}\\ =&b-\alpha\frac1m\sum_{i=1}^m({\color{orange}f}_{\vec w,b}(\vec x_i)-y_i) \end{align}\\~\\ 看上去和线性回归函数一样,但要注意的是这里的f的含义不同,这里的f是逻辑回归\\ Linear~regression:f_{\vec w,b}(x)=\vec w\cdot \vec x+b\\ Logistic~regression:{\color{orange}f}_{\vec w,b}(x)=\frac{1}{1+e^{-z}} 代价函数: J ( w , b ) = − m 1 i = 1 ∑ m [ − y i log ( f w , b ( x i )) − ( 1 − y i ) log ( 1 − f w , b ( x i ))] 梯度下降求偏导: w j = = b = = w j − α ∂ w j ∂ J ( w , b ) w j − α m 1 i = 1 ∑ m ( f w , b ( x i ) − y i ) x ij b − α ∂ b ∂ J ( w , b ) b − α m 1 i = 1 ∑ m ( f w , b ( x i ) − y i ) 看上去和线性回归函数一样,但要注意的是这里的 f 的含义不同,这里的 f 是逻辑回归 L in e a r re g ress i o n : f w , b ( x ) = w ⋅ x + b L o g i s t i c re g ress i o n : f w , b ( x ) = 1 + e − z 1
偏导的推导过程 计算图: J ( a , y ) = 1 m ∑ i m ( L ( a , y ) ) L ( a , y ) = − y log ( a ) − ( 1 − y ) log ( 1 − a ) a = σ ( z ) = 1 1 − e z z = w 1 x 1 + w 2 x 2 + b 一些中间变量: d a = d L d a = ( − y a + ( 1 − y ) ( 1 − a ) ) = a − y a ( 1 − a ) d z = d L d z = d L d a d a d z = a − y a ( 1 − a ) ⋅ a ( 1 − a ) = a − y 用于梯度下降的偏导数:(该例子中每次下降都要遍历m次) d w 1 = d L d z d z d w 1 = 1 m ∑ i m x 1 ( i ) ( a ( i ) − y ( i ) ) d w 2 = d L d z d z d w 2 = 1 m ∑ i m x 2 ( i ) ( a ( i ) − y ( i ) ) d b = d L d z d z d b = 1 m ∑ i m ( a ( i ) − y ( i ) ) 计算图:\\ \begin{aligned} J(a,y)=&\frac 1m \sum\limits_{i}^{m}(L(a,y))\\ L(a,y)=&-y\log(a)-(1-y)\log(1-a)\\ a=&\sigma(z)=\frac1{1-e^z}\\ z=&w_1x_1+w_2x_2+b \end{aligned}\\~\\~\\ 一些中间变量:\\ \begin{aligned} da=\frac{dL}{da}=&(-\frac{y}{a}+\frac{(1-y)}{(1-a)}) ~~~~~~~~~~~~~~~~~~~~~~=\frac{a-y}{a(1-a)}\\ {dz}=\frac{dL}{dz}=&\frac{dL}{da}\frac{da}{dz}=\frac{a-y}{a(1-a)}\cdot a(1-a) = a-y \end{aligned}\\~\\~\\ 用于梯度下降的偏导数:\text{(该例子中每次下降都要遍历m次)}\\ \begin{aligned} d{w_1}=&\frac{dL}{dz}\frac{dz}{dw_1}=\frac{1}{m}\sum\limits_{i}^{m}{x_{1}^{(i)}}({a}^{(i)}-{y}^{(i)})\\ d{w_2}=&\frac{dL}{dz}\frac{dz}{dw_2}=\frac{1}{m}\sum\limits_{i}^{m}{x_{2}^{(i)}}({a}^{(i)}-{y}^{(i)})\\ db=&\frac{dL}{dz}\frac{dz}{db}~~~=\frac{1}{m}\sum\limits_{i}^{m}{~~~~~~({a}^{(i)}-{y}^{(i)})}\\ \end{aligned} 计算图: J ( a , y ) = L ( a , y ) = a = z = m 1 i ∑ m ( L ( a , y )) − y log ( a ) − ( 1 − y ) log ( 1 − a ) σ ( z ) = 1 − e z 1 w 1 x 1 + w 2 x 2 + b 一些中间变量: d a = d a d L = d z = d z d L = ( − a y + ( 1 − a ) ( 1 − y ) ) = a ( 1 − a ) a − y d a d L d z d a = a ( 1 − a ) a − y ⋅ a ( 1 − a ) = a − y 用于梯度下降的偏导数: (该例子中每次下降都要遍历 m 次) d w 1 = d w 2 = d b = d z d L d w 1 d z = m 1 i ∑ m x 1 ( i ) ( a ( i ) − y ( i ) ) d z d L d w 2 d z = m 1 i ∑ m x 2 ( i ) ( a ( i ) − y ( i ) ) d z d L d b d z = m 1 i ∑ m ( a ( i ) − y ( i ) )
代码(for + 无框架) 代码流程:(假设有m个示例)
这里的代码片段仅计算一次梯度下降 。如果要梯度下降至收敛,还得再套一层循环
J = 0 ; dw1 = 0 ; dw2 = 0 ; db = 0 ; for i = 1 to m: z ( i ) = wx ( i ) + b; a ( i ) = sigmoid ( z ( i )); J += - [ y (i) log ( a (i)) + ( 1 - y (i)) log ( 1 - a (i)); dz (i) = a (i) - y (i); dw1 += x1 (i) dz (i); dw2 += x2 (i) dz (i); db += dz (i); J /= m; dw1 /= m; dw2 /= m; db /= m; w = w - alpha * dw; b = b - alpha * db; 代码(向量化 + 无框架) 向量化可以去除for循环,并节省几百倍的时间。
_
向量化的伪代码:
Z = w T X + b = n p . d o t ( w . T , X ) + b Z = w^{T}X + b = np.dot( w.T,X)+b Z = w T X + b = n p . d o t ( w . T , X ) + b
A = σ ( Z ) A = \sigma( Z ) A = σ ( Z )
d Z = A − Y dZ = A - Y d Z = A − Y
d w = 1 m ∗ X ∗ d z T {{dw} = \frac{1}{m}*X*dz^{T}\ } d w = m 1 ∗ X ∗ d z T
d b = 1 m ∗ n p . s u m ( d Z ) db= \frac{1}{m}*np.sum( dZ) d b = m 1 ∗ n p . s u m ( d Z )
w : = w − a ∗ d w w: = w - a*dw w := w − a ∗ d w
b : = b − a ∗ d b b: = b - a*db b := b − a ∗ d b
_
公式1~2完成了前向传播 ,对所有训练样本进行了预测,公式3~5完成了后向传播 ,对所有训练样本进行了求导,公式6~7完成了梯度下降 ,更新参数。